JUMP TO TOPIC
 A reflection of a function is a type of transformation of the graph of a function.
A reflection of a function is a type of transformation of the graph of a function.
The reflection of a function can be over the x-axis or y-axis, or even both axes. For example, the reflection of the function $y = f(x)$ can be written as $y = – f(x)$ or $y = f(-x)$ or even $y = – f(-x)$. There are four types of transformations of functions or graphs: Reflection, Rotation, Translation and Dilation.
In this guide, we will study the reflections of the function along with numerical examples so that you can grasp the concept quickly.
What Is a Reflection Function?
Reflection Function is the transformation of a function in which we flip the graph of the function around an axis. In mathematics or specifically in geometry, reflecting or reflection means flipping, so basically, reflection of a function is the mirror image of the given function or graph. Therefore, reflection functions are commonly known as reflecting functions.
Two graphs are said to be mirror images or reflections of each other if every point in one graph is equidistant from the corresponding point in the other graph. The reflection of the given function should be similar in size and shape to the original function.
The one feature that does not match is the direction. The direction of the reflected image or graph should be opposite to the original image or graph.
As we discussed earlier, there are four types of function transformations, and students often confuse the reflection of a function with the translation of a function. During the translation of a function, only the position of a function is changed while the size, shape, and direction remain the same.
On the other hand, during the reflection of a function, position as well as the direction of the image of the graph is changed while the shape and size remain the same.
Types of Reflection Function
There are three types of reflections of a function. Consider the function $y = f(x)$, it can be reflected over the x-axis as $y = -f(x)$ or over the y-axis as $y = f(-x)$ or over both the axis as $y = -f(-x)$.
Hence, we classify reflections of the function as:
- Reflection of a function over x – axis or vertical reflection
- Reflection of a function over y- axis or horizontal reflection
- Reflection of a function over x and y axis
All these types of reflections can be used for reflecting linear functions and non-linear functions.
How To Reflect a Function Over the X-axis
When we have to reflect a function over the x-axis, the points of the x coordinates will remain the same while we will change the signs of all the coordinates of the y-axis.
For example, suppose we have to reflect the given function $y = f(x)$ around the x-axis. In that case, the reflection over the x-axis equation for the given function will be written as $y = -f(x)$, and here you can see that all the values of “$y$” will have an opposite sign as compared to the original function. The reflection of a point $(x,y)$ over the x-axis will be represented as $(x,-y)$.
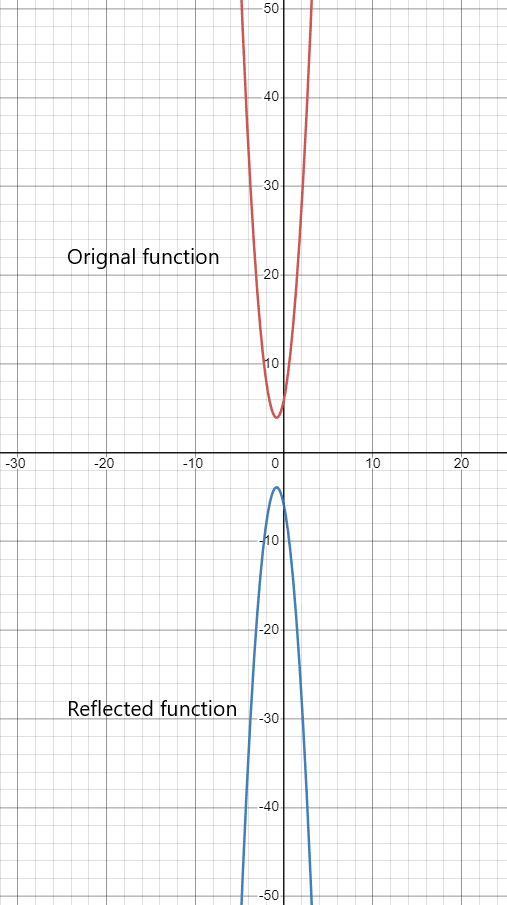
Allan was working as an architect engineer on a construction site and he just realized that the function $y = 3x^{2}+ 5x + 6$ he used to develop the blueprint/ graphical model of the site is incorrect and instead the correct function is $y = – ( 3x^{2} + 5x + 6)$.
Allan doesn’t have a computer at the site to simulate the function and obtain the relevant graph model. Still, Allan knows that it’s just a reflection of the original function over the x-axis, so he can easily draw the new graph by just changing the direction of the graph, which will keep all the corresponding points equidistant from each other.
The graphical representation of both functions is given below:
How to Reflect the Function Over the Y-axis
When we have to reflect a function over the y-axis, the points of the y coordinates will remain the same while we will change the signs of all the coordinates of the x-axis.
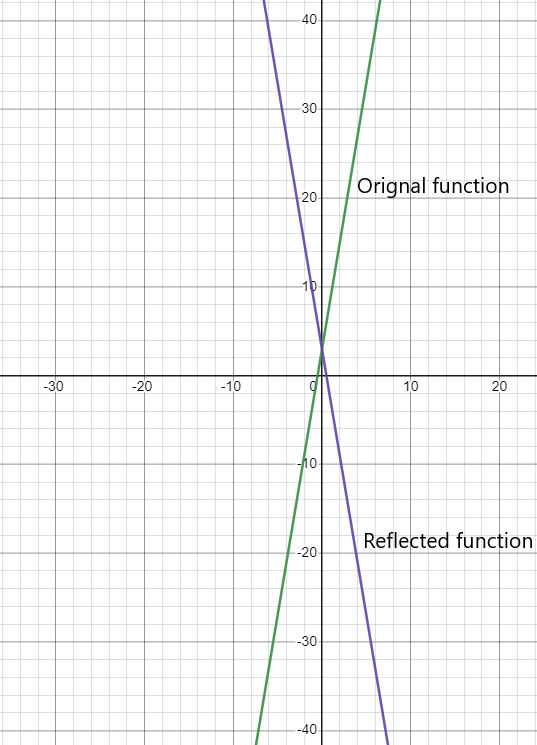
For example, if the function $y = f(x)$ is to be reflected over the y axis, then the resulting function will be $y = f(-x)$. As we can see, we are negating all the values of “x coordinates” in this case.
Consider a function $y = 6x + 3$, if we have to reflect this function over the y-axis, then the resulting function will be $y = -6x + 3$.
The graphical representation of both the functions is given below:
Reflection of a Function Over the X and Y-axis
When the function is to be reflected over the x and y-axis, we write it as a reflection of a function over $x = y$, so it is divided into two parts or two cases $y = x$ and $y = -x$.
When the graph of function is reflected over $y = x$, then we will swap the coordinates of the x and y-axis with each other while their signs remain the same. For example, we will write the reflection of a point $(3,4)$ as $(4,3)$.
When the graph of a function is reflected over $y = -x$, then the coordinates of the x and y-axis will be swapped with each other while there are also negated. For example, we will write the reflection of a point $(3,4)$ as $(-4,-3)$.
So if we are given a function $y = f(x)$ and you are asked to reflect this function over both x and y axis, then the resulting function will be $y = -f(-x)$.
Consider a function $y = 6x + 3$, if we have to reflect this function over both x and y-axis, then the resulting function will be $y = -(-6x + 3)$.
Example 1:
You are given the tabular values of the three functions $f(x)$, $g(x)$ and $h(x)$. The original function is f(x). Determine the type of reflection used to form the other two functions.
| x | $3$ | $1$ | $2$ | $6$ | $8$ |
| f(x) | $6$ | $1$ | $2$ | $9$ | $12$ |
| x | $3$ | $1$ | $2$ | $6$ | $8$ |
| g(x) | $-6$ | $-1$ | $-2$ | $-9$ | $-12$ |
| x | $-3$ | $-1$ | $-2$ | $-6$ | $-8$ |
| h(x) | $-5$ | $-2$ | $-3$ | $-6$ | $-8$ |
Solution:
We are given three functions, $f(x)$, $g(x)$ and $h(x)$, along with corresponding values of $x$.
The function f(x) is the original function, and we will use it in comparison to other functions to determine the type of reflection performed on other functions.
The function g(x) has the opposite values as compared to the function $f(x)$, while the values of “x” are the same. Hence we can write $g(x) = – f(x)$, so it shows that the original function is reflected over x-axis in this case.
For the function $h(x)$, the values of “$x$” are negative as compared to values of “x” for the original function $f(x)$. The values h(x) do not guarantee whether the original function is reflected over the y-axis or over $y = -x$, so it can be both reflection over the y axis or $y = -x$ as we don’t have the actual function to calculate the values.
Example 2:
Draw the reflections of the given functions over the x-axis and y-axis
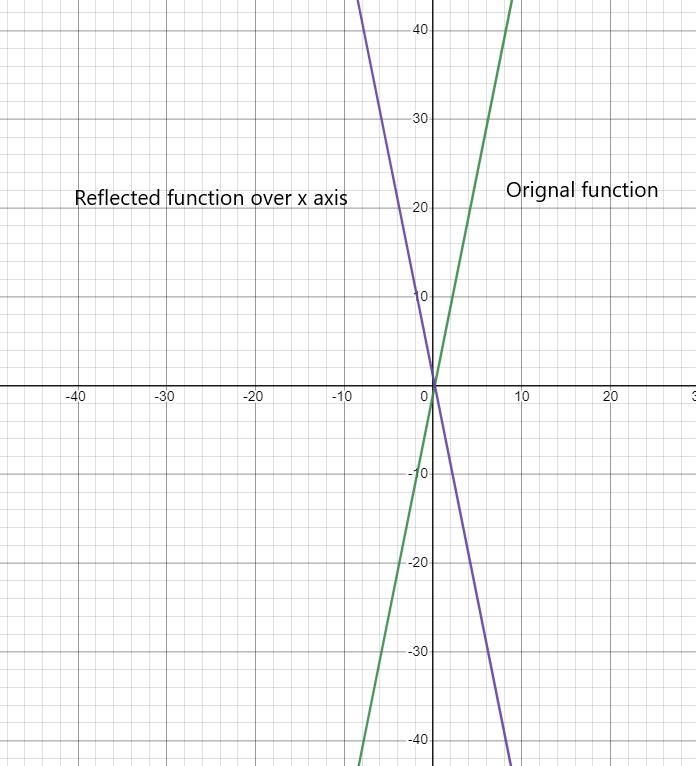
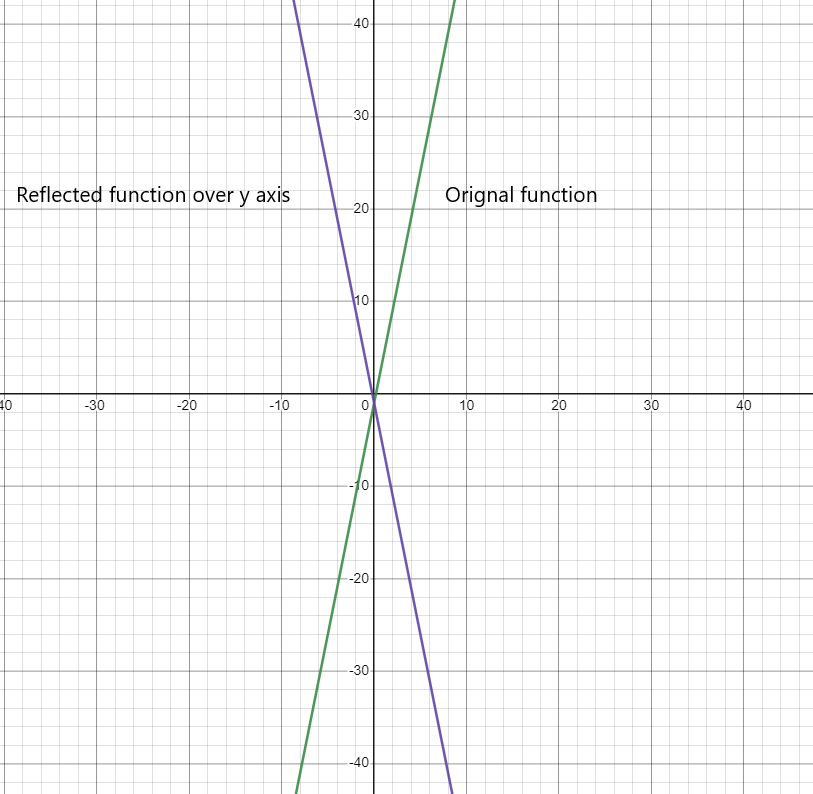
- $y = 5x -1$
- $y = 5x^{2}- 3x +2$
Solution:
1)
Reflection of function over the x-axis:
Reflection of function over the y-axis:
2)
Reflection of function over the x-axis:
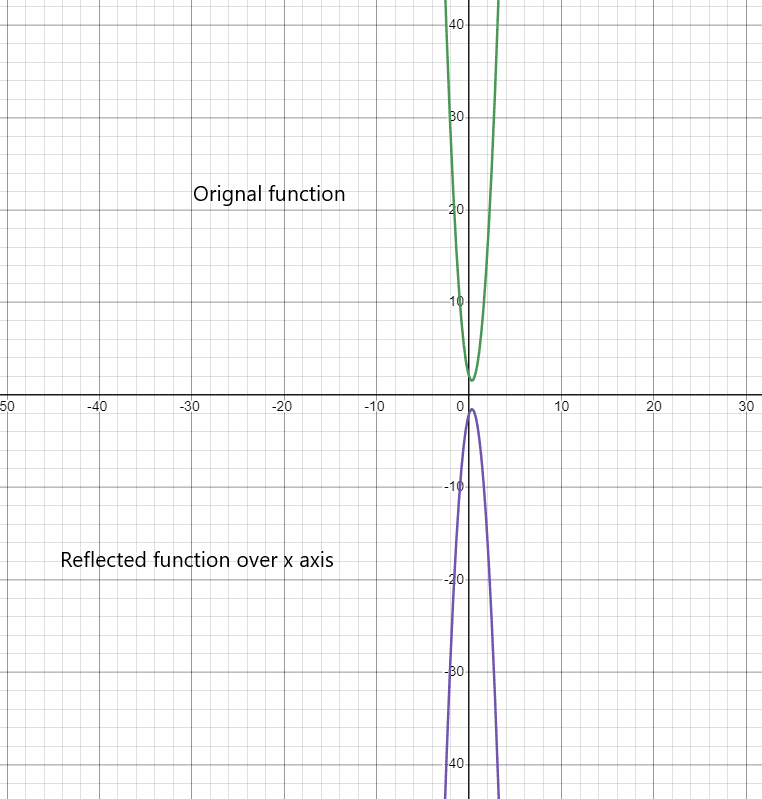
Reflection of function over the y-axis:
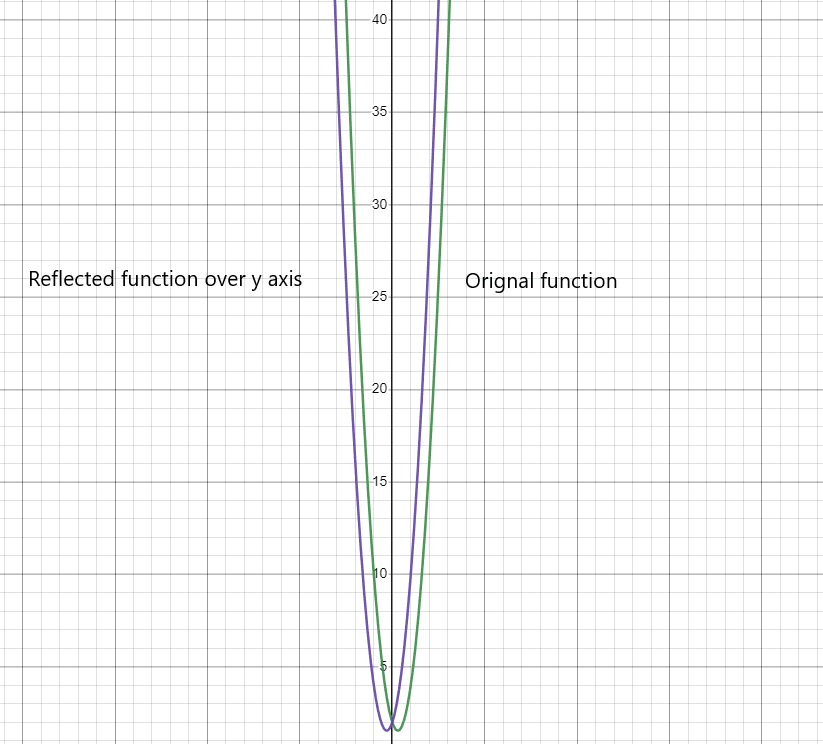
Example 3:
Write the reflections of the given functions over the x-axis, y-axis, and both x and y-axis.
- $y = 6x -3$
- $y = 7x^{2}+3x + 2$
Solution:
1)
When the function $y = 6x -3$ is reflected across the x-axis, then it will be written as $y = -(6x-3)$.
When the function $y = 6x -3$ is reflected across the y-axis, then it will be written as $y = (-6x-3)$.
When the function $y = 6x -3$ is reflected across the both axis, then it will be written as $y = -(-6x-3)$.
2)
When the function $y = 5x^{2}- 3x +2$ is reflected across the x-axis, then it will be written as $y = -(5x^{2}- 3x +2)$.
When the function $y = 5x^{2}- 3x +2$ is reflected across the y-axis, then it will be written as $y = 5(-x)^{2}- 3(-x) +2$.
When the function $y = 5x^{2}- 3x +2$ is reflected across the both axis, then it will be written as $y = -(5(-x)^{2}- 3(-x) +2)$.
Practice Questions
1) You are given the tabular values of the three functions f(x), g(x), and h(x). The original function is f(x). You must determine the type of reflection used to form the other two functions.
| x | $3$ | $1$ | $2$ | $6$ | $8$ |
| f(x) | $6$ | $1$ | $2$ | $9$ | $12$ |
| x | $3$ | $1$ | $2$ | $6$ | $8$ |
| g(x) | $-6$ | $-1$ | $-2$ | $-9$ | $-12$ |
2) You are required to write the reflections of the given functions over the x-axis, y-axis and both x and y axis.
- $y = 7x – 5$
- $y = 6x^{2}-2x +2$
- $y = -(7x^{2}+4x -1)$
Answer Key:
1)
The function $f(x)$ is the original function, and we will use it in comparison to other functions to determine the type of reflection performed on other functions.
2)
a) When the function $y = 7x -5$ is reflected across the x-axis, then it will be written as $y = -(7x-5)$.
When the function $y = 7x -5$ is reflected across the y-axis, then it will be written as $y = (-5x-5)$.
When the function $y = 7x -5$ is reflected across the both axis, then it will be written as $y = -(-7x-5)$.
b)
When the function $y = 6x^{2}- 2x +2$ is reflected across the x-axis, then it will be written as $y = -(6x^{2}- 2x +2)$.
When the function $y = 6x^{2}- 2x +2$ is reflected across the y-axis, then it will be written as $y = 6(-x)^{2}- 2(-x) +2$.
When the function $y = 6x^{2}- 2x +2$ is reflected across the both axis, then it will be written as $y = -(6(-x)^{2}- 2(-x) +2)$.
c)
When the function $y = -(7x^{2}+4x -1)$ is reflected across the x-axis, then it will be written as $y = (7x^{2}+4x -1)$.
When the function $y = -(7x^{2}+4x -1)$ is reflected across the y-axis, then it will be written as $y = -(7(-x)^{2}+4(-x) -1)$.
When the function $y = -(7x^{2}+4x -1)$ is reflected across the both axis, then it will be written as $y = -(7(-x)^{2}+4(-x) -1)$.
