Relative Extrema – Definition, Properties, and Examples

The concept of relative extrema, also known as local extrema, is a key player in calculus that offers valuable insights into the local behavior of functions. These extrema signify a function’s local maximum and minimum values, providing a nuanced comprehension of its shape, trend, and turning points.

Understanding the peaks and valleys of functions is critical to mathematical analysis, allowing us to unravel intricate behaviors of diverse phenomena across multiple disciplines. From optimizing complex systems in engineering to understanding population dynamics in ecology and even unraveling economic trends, the concept of relative extrema has far-reaching implications.

This article dives deep into the fascinating world of relative extrema, revealing the underpinning theory, exploring identification methods, and illustrating their myriad applications across fields.

Definition of Relative Extrema

Relative extrema, or local extrema, are points in a function where the function takes on a local maximum or minimum value. In simpler terms, a point on the function’s graph with a peak or valley is a relative extremum. There are two types of relative extrema: relative maxima and relative minima.

It’s important to note that a function may have many relative extrema or none. Moreover, relative extrema are “local” in that they represent the highest or lowest points only within a certain range of the function and not necessarily the absolute highest or lowest points of the entire function.

Below we present the generic representation of relative extrema in figure-1.

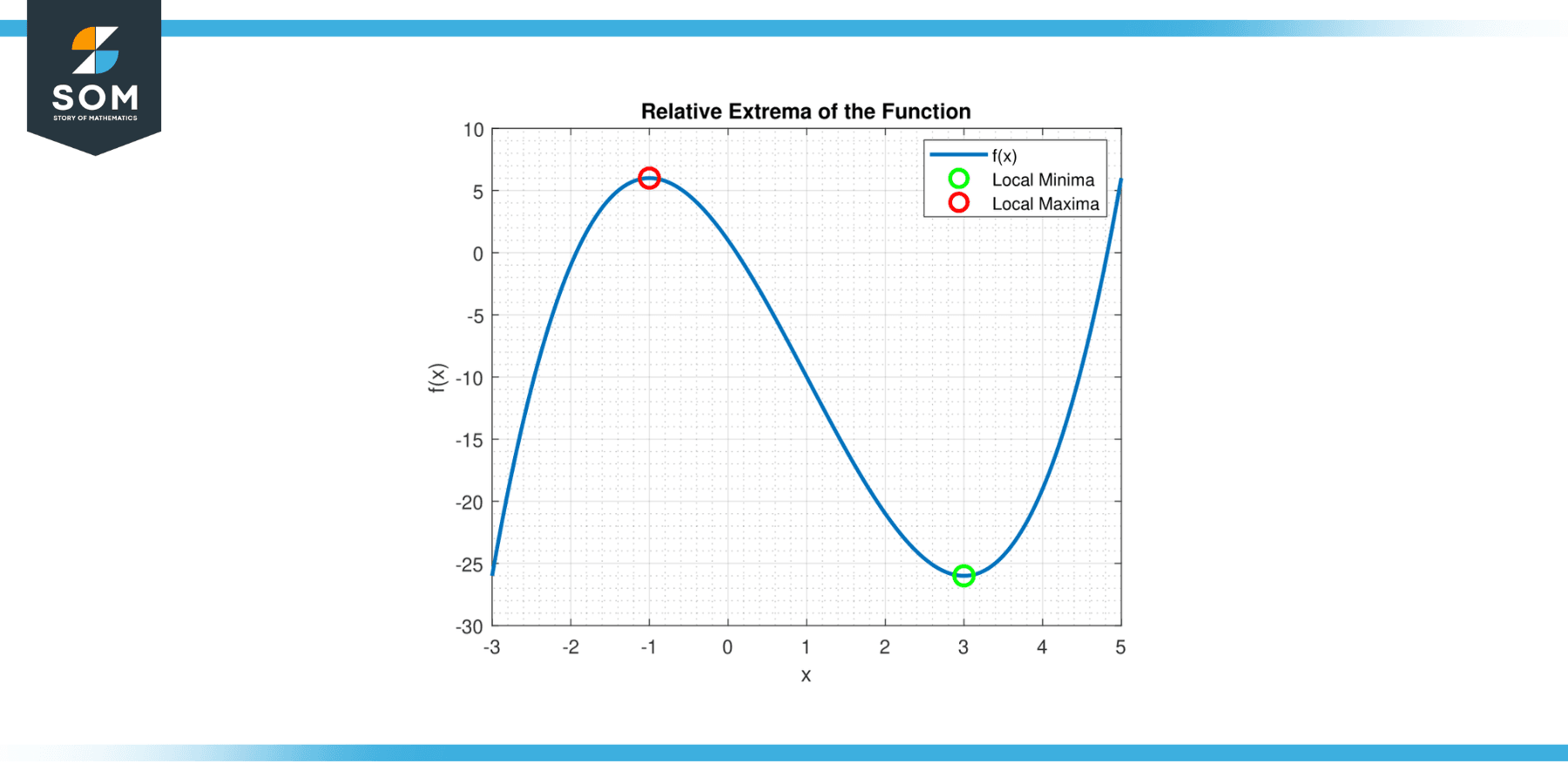
Figure-1.

Historical Significance

Relative extrema, which refers to a function’s local minimum or maximum, are a key concept in calculus. The concept of extrema (relative/local and absolute/global) is implicitly connected to the understanding and development of calculus.

The formal study of calculus, which includes the concepts of relative extrema, began with the works of Sir Isaac Newton and Gottfried Wilhelm Leibniz in the 17th century. Newton and Leibniz independently developed the fundamental principles of calculus, though their notation and approach varied slightly.

Newton called his calculus “the science of fluxions,” and his notation is not the one commonly used today. On the other hand, much of Leibniz’s notation, such as dx and dy, is still in use.

While Newton primarily used calculus to develop his laws of motion and gravitation, Leibniz saw it more as a mathematical system, and his works form a substantial part of the basis of mathematical analysis, where the study of extrema plays a crucial role.

The concept of extrema became more nuanced with the further development of calculus. The works of mathematicians like Augustin-Louis Cauchy, Karl Weierstrass, and others in the 19th century helped to provide a more rigorous foundation for calculus, including the concept of extrema.

The definition and properties of extrema were solidified, including the distinction between relative and absolute extrema, and important theorems were proven, such as the Extreme Value Theorem and Fermat’s Theorem (which provides conditions under which a function will have an extremum at a given point).

Today, the concept of relative extrema is taught in calculus courses worldwide and is used in numerous applications across various fields, from physics to economics, demonstrating the enduring impact of these early mathematical pioneers.

Types of Relative Extrema

Relative extrema, also called local extrema, comes in the following two types:

Relative (Local) Maxima

A relative maximum of a function is a point where the function’s value is greater than or equal to all other points in its immediate vicinity. In other words, a point in the function is a relative maximum if the function’s value at that point is higher than the function’s values at nearby points.

It’s the peak of a hill when you’re hiking – there might be higher points (global maxima) elsewhere, but it’s the highest point in your local area.

Relative (Local) Minima

A relative minimum of a function is a point where the function’s value is less than or equal to all other points in its immediate vicinity. Similar to the relative maximum, a relative minimum is a point at which the function’s value is lower than the function’s values at nearby points.

It’s like the bottom of a valley when you’re hiking – there might be lower points (global minima) elsewhere, but it’s the lowest point in your local area.

It’s important to remember that these are “local” or “relative” extrema, meaning they are the highest or lowest points within a certain range or interval. This contrasts “global” or “absolute” extrema, representing the entire function’s overall highest or lowest point.

Properties of Relative Extrema

Relative extrema, or local extrema, are points in a function’s graph where the function takes on local maximum or minimum values. Here are some important properties:

Existence

Not all functions have relative extrema. For example, the function f(x) = x has no relative maximum or minimum because it steadily increases from negative to positive infinity. However, the Extreme Value Theorem guarantees continuous functions on a closed interval [a, b] have at least one relative extremum.

Types

There are two types of relative extrema: relative maxima and relative minima. At a relative maximum, the function value is greater than or equal to the values at nearby points, while at a relative minimum, the function value is less than or equal to the values at nearby points.

Location

Relative extrema occur when the function changes direction, either from increasing to decreasing or vice versa. These points are often, but not always, where the derivative of the function is zero (these are called critical points) or where the derivative is undefined.

First Derivative Test

If a function’s derivative changes sign from positive to negative at a point, then the function has a relative maximum. The function has a relative minimum if the derivative changes sign from negative to positive at a point. This is known as the First Derivative Test.

Second Derivative Test

If a function’s first derivative is zero at a point and its second derivative is negative at that point, it has a relative maximum. The function has a relative minimum if the first derivative is zero and the second derivative is positive. This is known as the Second Derivative Test. However, the test is inconclusive if the second derivative is zero or undefined.

Countability

A function can have any countable number of relative extrema. For example, the function f(x) = sin(x) has infinitely many relative maxima and minima.

Local Behavior

Relative extrema give insights into the local behavior of a function. They provide information about the function’s trend (increasing or decreasing) and turning points within certain intervals.

Global vs. Local

Relative extrema are “local” in that they are the highest or lowest points within a certain range of the function. They may or may not be the absolute highest or lowest points of the entire function, called global or absolute extrema.

Understanding these properties of relative extrema is crucial in calculus, especially when dealing with optimization problems, curve sketching, physical motion, economics, and other applications.

Applications 

Relative extrema play a significant role in many different fields of study. Here are a few examples:

Physics and Engineering

In physics and engineering, relative extrema can be used to optimize various scenarios, such as maximizing efficiency or minimizing waste. For example, you can use relative extrema to determine the highest point a projectile will reach (relative maximum) or the best shape for a can to minimize the material used while maximizing volume (an optimization problem).

Economics and Business

Economists use relative extrema to maximize profit or minimize cost. For example, a business might use calculus to find a relative minimum of a cost function to minimize production costs. Conversely, they might find a relative maximum of a revenue function to maximize income.

Biology and Medicine

Relative extrema can help understand and predict population growth or disease spread in biology and medicine. For instance, a relative maximum can indicate the highest number of species in a certain habitat, while a relative minimum can indicate the lowest.

Computer Science

In machine learning and data science, algorithms often need to find the minimum or maximum of a function to optimize model performance. For example, gradient descent algorithms aim to find a relative minimum in the loss function, improving the model’s predictions.

Environmental Science

In environmental studies, relative extrema can help understand and predict patterns like temperature changes, pollution levels, and more. For example, the highest and lowest temperatures would be relative maxima and minima over a given period.

Chemistry

In thermodynamics, relative extrema can help find stable energy states. For instance, relative minima of potential energy surfaces correspond to stable configurations of molecules.

These examples illustrate the broad scope and importance of relative extrema in understanding and optimizing the world around us.

Exercise 

Example 1

Compute the relative extrema of the function f(x) = x².

Solution

Taking the derivative of the function:

f'(x) = 2x

we set it equal to zero to find the critical points:

2x = 0

sox = 0 Is this our only critical point?

The second derivative is:

f''(x) = 2

Since it’s positive, x = 0 it is a relative minimum by the second derivative test.

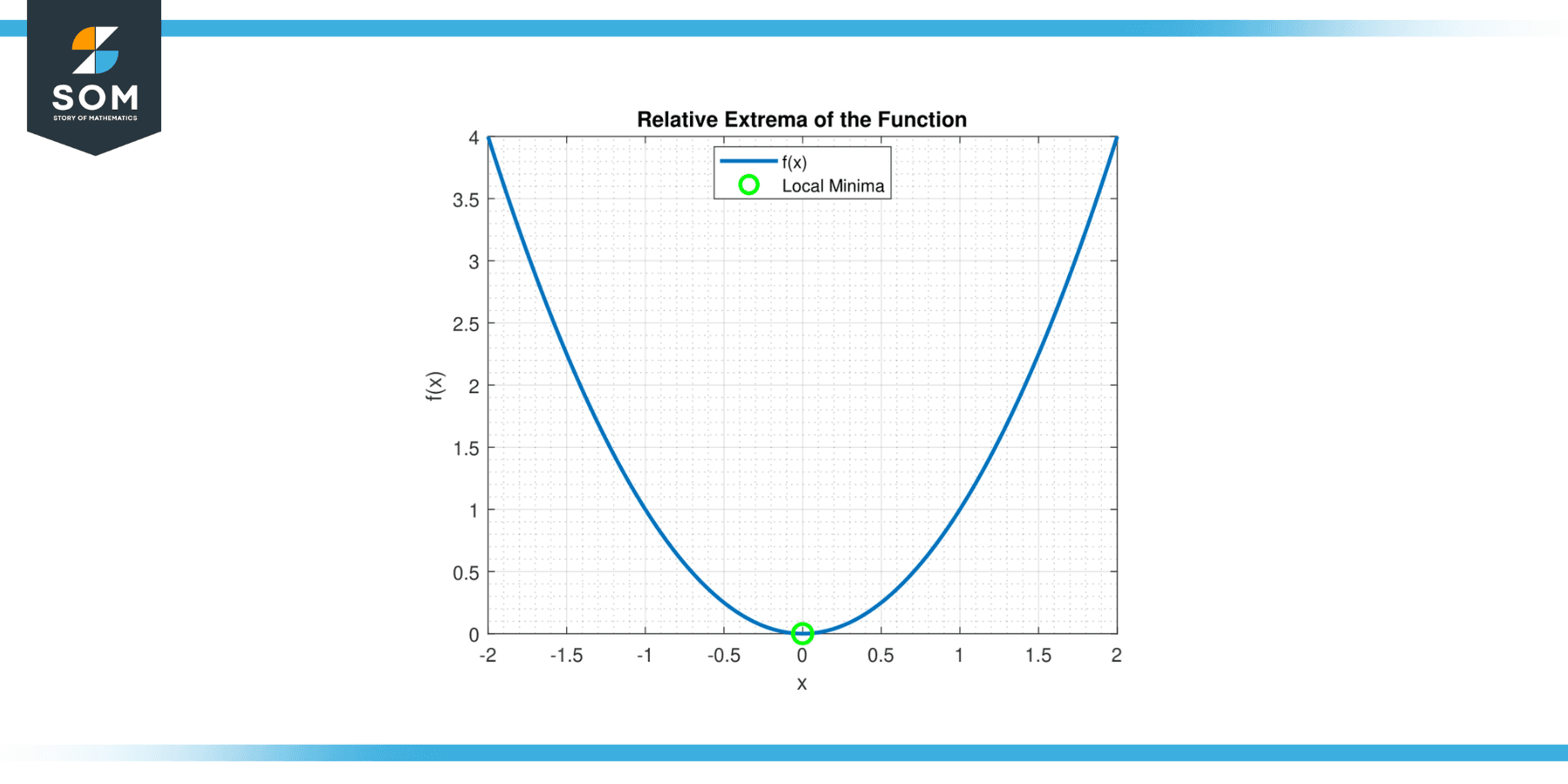
Figure-2.

Example 2

Compute the relative extrema of the function f(x) = -x².

Solution

Taking the derivative of the function:

f'(x) = -2x

we set it equal to zero to find the critical points:

-2x = 0

so x = 0 is our only critical point?

The second derivative is:

f''(x) = -2

Since it’s negative, x = 0 it is a relative maximum by the second derivative test.

Example 3

Determine the relative extrema of the function f(x) = x³.

Solution

Taking the derivative of the function:

f'(x) = 3x²

we set it equal to zero to find the critical points:

3x² = 0

 so x = 0 is our only critical point?

The second derivative is:

f''(x) = 6x

At x = 0, the second derivative is also zero, so the second derivative test is inconclusive.

By examining the function, we see that f(x) decreases for x < 0 and increases, so there is no relative maximum or minimum at x = 0.

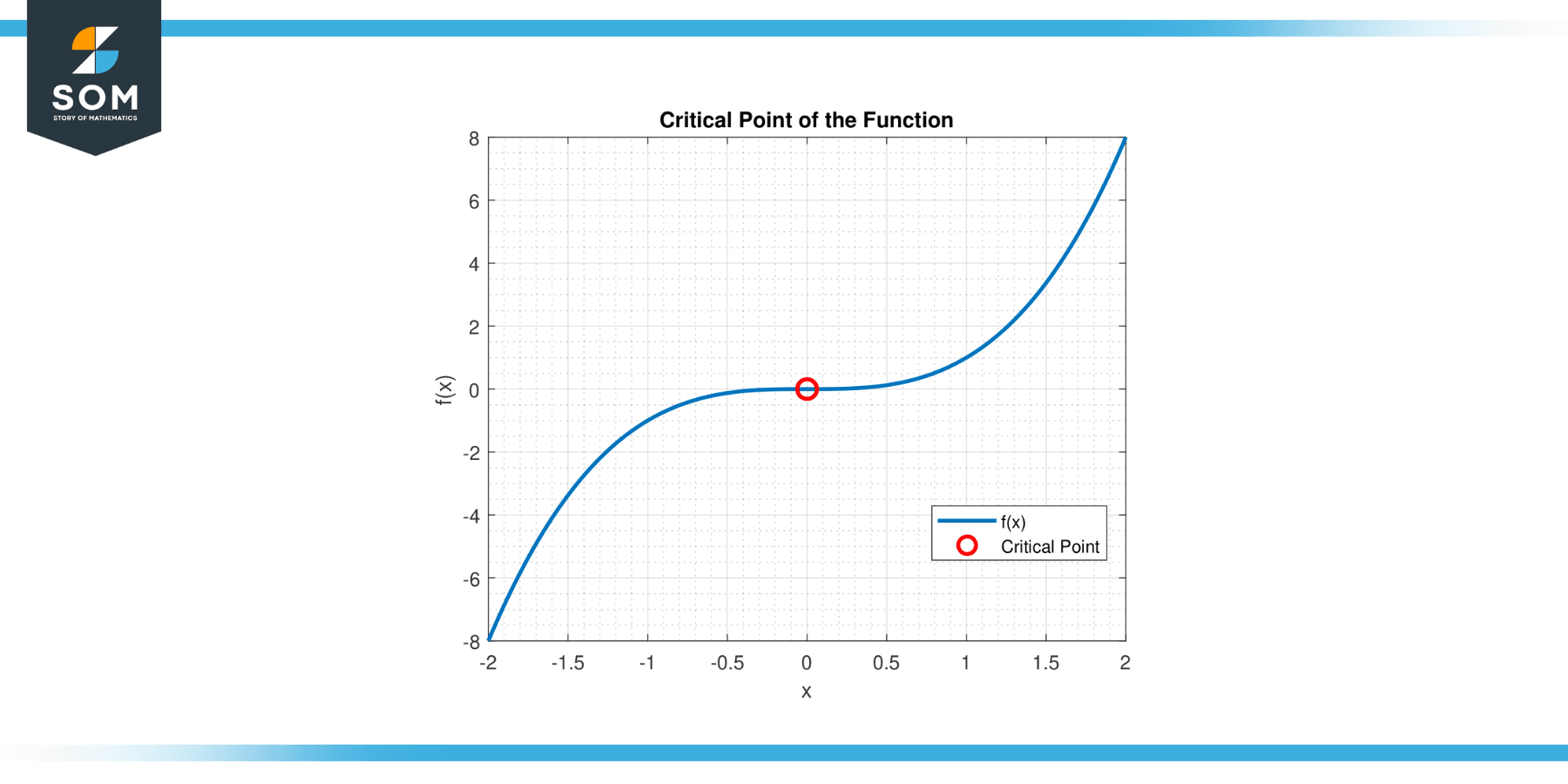
Figure-3.

Example 4

Determine the relative extrema of the function. f(x) = x⁴.

Solution

Taking the derivative of the function:

f'(x) = 4x³

 we set it equal to zero to find the critical points:

4x³ = 0

so x = 0 is our only critical point?

The second derivative is:

f''(x) = 12x

At x = 0, the second derivative is zero, so the second derivative test is inconclusive.

However, since the function f(x) is always nonnegative,  x = 0 it is a relative (and absolute) minimum.

Example 5

Compute the relative extrema of the function f(x) = sin(x) on the interval [0, 2π].

Solution

The derivative of the function:

f'(x) = cos(x)

which equals zero at x = π/2 and x = 3π/2.

At x = π/2,:

f''(x) = -sin(x) < 0

so x = π/2 is a relative maximum.

At x = 3π/2:

f''(x) = -sin(x) > 0

so x = 3π/2 is a relative minimum.

Example 6

Find the relative extrema of the function f(x) = x⁵ - 5x³.

Solution

The derivative of the function:

f'(x) = 5x⁴ – 15x²

set this to zero to find the critical points:

5x⁴ - 15x² = 0

gives us:

x² (5x² - 15) = 0

Hence, the critical points are x = 0, x = √(3), and x = -√(3).

The second derivative is:

f''(x) = 20x³ - 30x

Evaluating this at our critical points, we have:

• At x = 0, f''(0) = 0, so the second derivative test is inconclusive.
• At x = √(3), f''(√(3)) = 60 - 30 √(3) < 0, sox = √(3) is a relative maximum.
• At x = -√(3), f''(-√(3)) = -60 - 30 √(3) < 0, so x = -√(3) is a relative maximum.

Example 7

Determine the relative extrema of the function f(x) = x / (x² + 1).

Solution

The derivative of the function:

f'(x) = (1 - x²) / (x² + 1)^2

Set this to zero to find the critical points:

(1 - x²) = 0

gives us x = -1 and x = 1.

The second derivative is:

f''(x) = -4x / (x² + 1)^3

 Evaluating this at our critical points, we have:

• At x = -1, f''(-1) = 4 / 2^3 = 0.5 > 0, so x = -1 is a relative minimum.
• At x = 1, f''(1) = -4 / 2^3 = -0.5 < 0, so x = 1 is a relative maximum.

Example 8

Compute the relative extrema of the function f(x) = 3x⁴ - 4x³.

Solution

The derivative of the function:

f'(x) = 12x³ - 12x²

Set this to zero to find the critical points:

12x³ - 12x² = 0

gives us x = 0 and x = 1.

The second derivative is:

f''(x) = 36x² - 24x

Evaluating this at our critical points, we have:

• At x = 0, f''(0) = 0, so the second derivative test is inconclusive.
• At x = 1, f''(1) = 36 - 24 = 12 > 0, so x = 1 is a relative minimum.

 

All images were created with MATLAB.