JUMP TO TOPIC
The second derivative implicit differentiation is a powerful tool to differentiate implicitly defined functions concerning an independent variable not explicitly expressed. Exploring the intricacies of calculus often leads us to fascinating techniques that unveil the hidden properties of equations and functions.
While implicit differentiation enables us to find the first derivative of such functions, delving deeper into the realm of calculus reveals the significance of the second derivative.
In this article, we embark on a journey to explore the realm of second derivative implicit differentiation, unraveling its insights, applications, and profound impact in unraveling the mysteries hidden within implicit equations.
Defining Second Derivative Implicit Differentiation
Second derivative implicit differentiation is a technique used in calculus to find the second derivative of an implicitly defined function. When an equation relates the dependent variable y to the independent variable x without explicitly expressing y as a function of x, implicit differentiation allows us to differentiate both sides of the equation with respect to x.
By applying the chain rule and differentiating term by term, we can find the first derivative of y with respect to x. We differentiate the first derivative through implicit differentiation to obtain the second derivative. This technique allows us to analyze implicitly defined curves’ concavity and inflection points and better understand their behavior.
By exploring the second derivative implicitly, we can uncover important information about the shape and curvature of curves that might not be easily derived through explicit differentiation.
Below we present a generic representation of the second derivative implicit differentiation in figure-1.
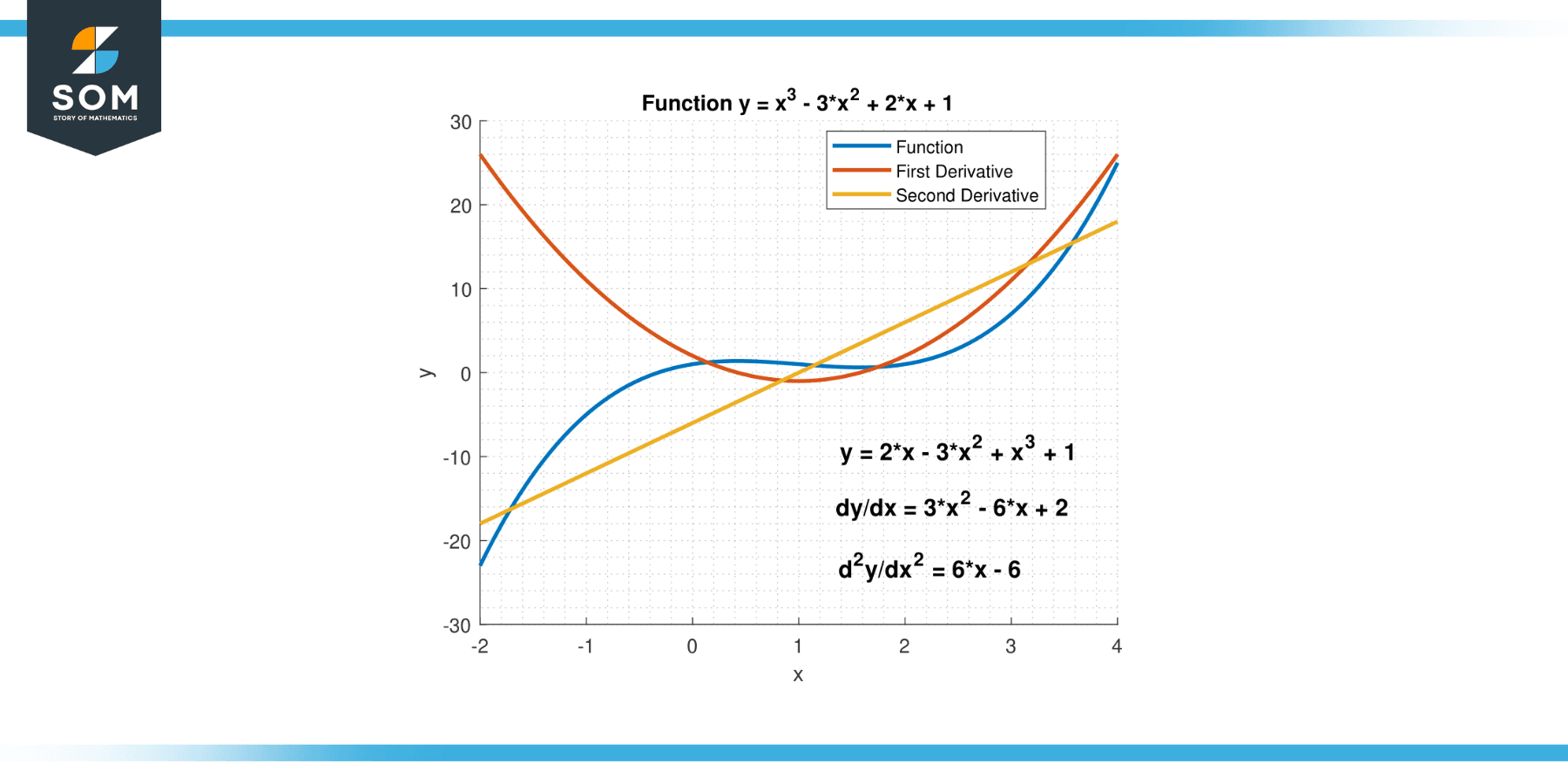
Figure-1.
Evaluating Second Derivative Implicit Differentiation
Evaluating the second derivative using implicit differentiation involves differentiating the equation twice with respect to the independent variable, usually denoted as x. Here’s a step-by-step guide to the process:
Start With the Implicitly Defined Equation
This equation relates the dependent variable, typically denoted as y, to the independent variable x without explicitly expressing y as a function of x.
Differentiate the Equation Implicitly
To find the first derivative of y with respect to x, differentiate both sides of the equation with respect to x. Treat y as a function of x when differentiating and apply the chain rule whenever necessary.
Solve for dy/dx
After differentiating, rearrange the equation to solve for dy/dx, which represents the first derivative of y with respect to x.
Differentiate the Equation Again
To find the second derivative, differentiate the equation obtained in step 3. Apply the derivative rules, including the product rule, chain rule, and power rule, as needed.
Simplify the Expression
Simplify the resulting expression for the second derivative by combining like terms, factoring out common factors, and performing any necessary algebraic manipulations.
Finalize the Second Derivative
Express the second derivative in a simplified and concise form, ensuring that it represents the derivative of y with respect to x.
Properties
Here are the properties of second derivative implicit differentiation explained in detail:
Implicitly Defined Equations
Second derivative implicit differentiation is used when we have an equation that relates the dependent variable y to the independent variable x without explicitly expressing y as a function of x. This can occur when dealing with curves or surfaces that cannot be easily expressed as explicit functions.
Applying Implicit Differentiation
To find the first derivative of y with respect to x, we differentiate both sides of the implicitly defined equation with respect to x. The chain rule is applied to terms involving y, treating y as a function of x and taking its derivative.
Differentiating Term by Term
When differentiating the equation term by term, we treat y as a function of x and apply the product rule, chain rule, and power rule as necessary. The derivatives of x terms result in 1, and y terms are expressed as dy/dx.
Finding the Second Derivative
Once the first derivative of y with respect to x is obtained through implicit differentiation, we can differentiate it again to find the second derivative. This involves applying the chain rule and other derivative rules as needed.
Analyzing Concavity
The second derivative obtained from implicit differentiation helps determine the concavity of the curve or surface defined implicitly. If the second derivative is positive, the curve is concave upward, indicating a bottom point in the curve. If the second derivative is negative, the curve is concave downward, representing a top point in the curve.
Inflection Points
Inflection points are locations on a curve where the concavity changes. By examining the second derivative implicitly, we can identify the x-values at which the second derivative changes sign, indicating the presence of inflection points.
Curvature
The second derivative implicitly provides insights into the curve’s curvature or surface. Positive values of the second derivative indicate that the curve is bending conclusively, while negative values indicate concave bending.
Higher Order Derivatives
The second derivative implicit differentiation technique can be extended to find higher-order derivatives implicitly. We can derive third, fourth, or higher-order derivatives as needed by repeatedly differentiating the implicitly defined equation.
By leveraging the properties of second derivative implicit differentiation, we can gain a deeper understanding of the behavior, concavity, inflection points, and curvature of curves and surfaces defined implicitly. It provides a powerful tool to analyze complex equations and uncover valuable insights that might not be easily obtained through explicit differentiation.
Applications
Second derivative implicit differentiation finds applications in various fields where implicitly defined relationships are encountered. Here are some examples of its applications in different fields:
Physics and Engineering
In physics and engineering, many physical phenomena are described by implicit equations. Second derivative implicit differentiation allows us to analyze the curvature, inflection points, and concavity of curves or surfaces that arise in motion, forces, fluid flow, and more. This information helps in understanding the behavior and characteristics of physical systems.
Economics and Finance
Implicit relationships often arise in economic and financial models. By employing second derivative implicit differentiation, economists and financial analysts can examine the concavity and curvature of cost functions, production functions, utility functions, and other implicit equations. This aids in understanding the behavior of economic variables and optimizing decision-making processes.
Biological Sciences
Implicit equations frequently appear in biological models, such as population dynamics, growth patterns, and biochemical reactions. Second derivative implicit differentiation allows researchers to investigate these models’ curvature and inflection points, providing insights into critical thresholds, stability, and critical points that determine biological behavior.
Computer Graphics and Animation
Implicit equations are utilized in computer graphics and animation to represent complex shapes and surfaces. Second derivative implicit differentiation helps determine these surfaces’ curvature and shading properties, enhancing the realism and visual quality of rendered objects.
Machine Learning and Data Analysis
Implicit equations arise in machine learning algorithms and data analysis when dealing with complex relationships between variables. Second derivative implicit differentiation aids in analyzing the curvature and inflection points of these relationships, enabling the identification of critical features, optimal parameter settings, and decision boundaries.
Geometric Modeling
In geometric and computer-aided design, implicit equations define curves and surfaces. Second derivative implicit differentiation is vital in determining the curvature, tangents, and inflection points of these curves and surfaces, ensuring accurate representations and smooth interpolation.
Optics and Wave Propagation
Implicit equations are encountered in optics and wave propagation phenomena, such as light refraction, diffraction, and waveguides. Second derivative implicit differentiation assists in studying the curvature and concavity of wavefronts, aiding in the design and analysis of optical systems.
Mathematics Education and Research
Second derivative implicit differentiation is an important concept in calculus education and research. It deepens the understanding of differentiation techniques, introduces the concept of concavity, and expands students’ problem-solving abilities. Researchers also explore the mathematical properties and behaviors of implicitly defined equations using second derivative implicit differentiation.
These applications demonstrate the significance of second derivative implicit differentiation in diverse fields, enabling a deeper analysis of complex relationships, shapes, and phenomena beyond explicit functions. It is a powerful tool for gaining insights, making predictions, and optimizing various scientific, engineering, and mathematical processes.
Exercise
Example 1
Consider the equation x² + y² = 25. Find the second derivative of y with respect to x.
Solution
To find the second derivative, we need to differentiate the equation twice with respect to x.
First, implicitly differentiate the equation once to find the first derivative:
2x + 2y * dy/dx = 0
Solving for dy/dx, we get:
dy/dx = -x/y
Now, we differentiate the equation again to find the second derivative:
2 + 2(dy/dx)^2 + 2y * d²y/dx² = 0
Substituting dy/dx = -x/y, we have:
2 + 2(-x/y)² + 2y * d²y/dx² = 0
Simplifying, we get:
d²y/dx² = (2y² – 2x²) / y³
Therefore, the second derivative of y with respect to x is d²y/dx² = (2y² – 2x²) / y³.
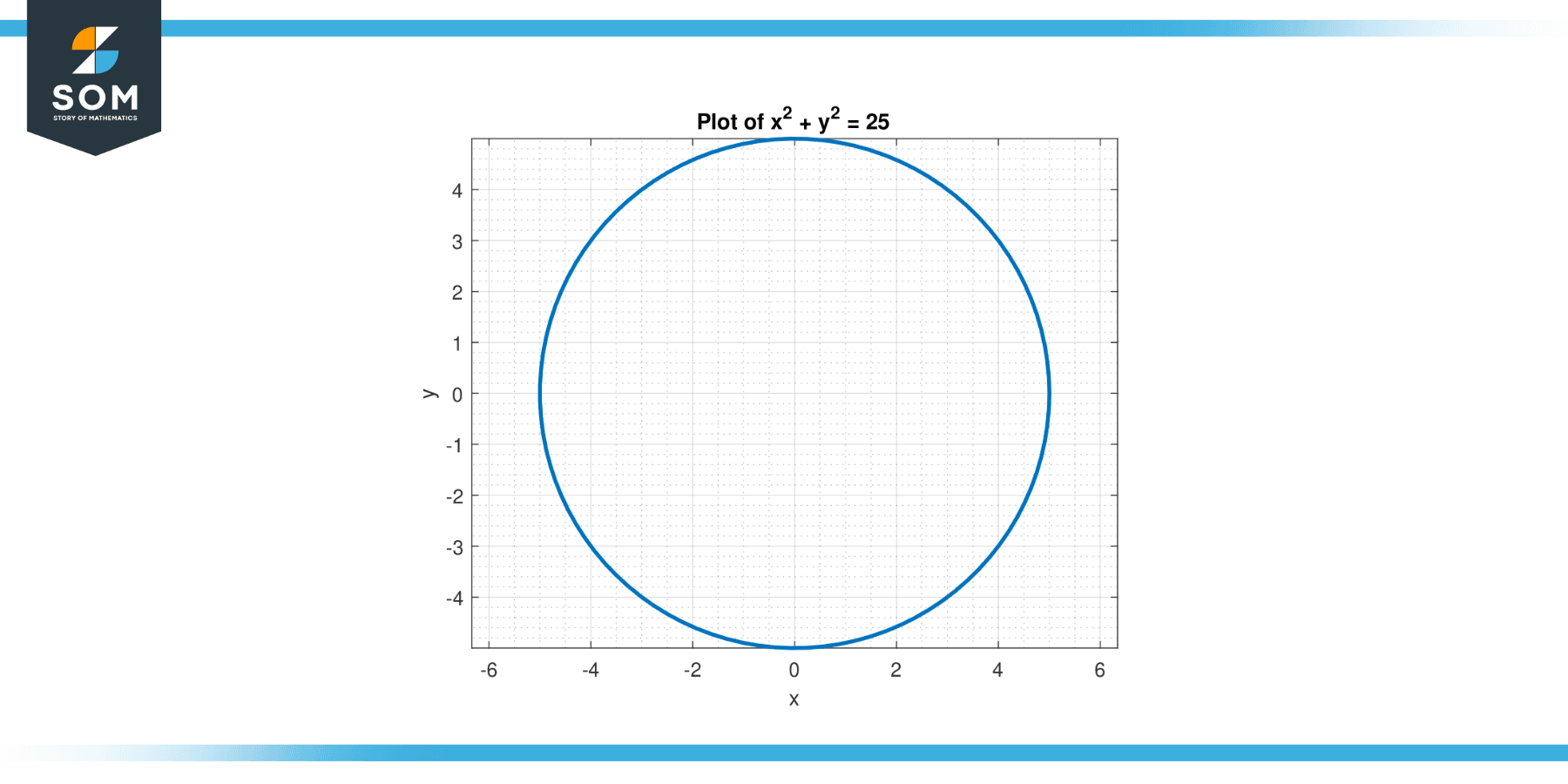
Figuer-2.
Example 2
Consider the equation x³ + y³ – 9xy = 0. Find the second derivative of y with respect to x.
Solution
Differentiate the equation implicitly to find the first derivative:
3x² + 3y² * dy/dx – 9(dy/dx) * y – 9x = 0
Rearranging, we get:
dy/dx = (9x – 3x²) / (3y² – 9y)
Now, differentiate the equation again to find the second derivative:
d²y/dx² = [(9 – 6x) * (3y² – 9y) – (9x – 3x²) * (6y – 9)] / (3y² – 9y)²
Therefore, the second derivative of y with respect to x is given by the expression [(9 – 6x) * (3y² – 9y) – (9x – 3x²) * (6y – 9)] / (3y² – 9y)².
Example 3
Consider the equation x² – 2xy +y² + 2x – 2y = 0. Find the second derivative of y with respect to x.
Solution
Differentiate the equation implicitly to find the first derivative:
2x – 2y – 2y * dy/dx + 2 – 2 * dy/dx = 0
Simplifying, we get:
dy/dx = (2x + 2 – 2y) / (2 – 2y)
Now, differentiate the equation again to find the second derivative:
d²y/dx² = [(2 – 2y) * (2 – 2 * dy/dx) – (2x + 2 – 2y) * (-2 * dy/dx)] / (2 – 2y)²
Simplifying further, we obtain the expression:
d²y/dx² = 4 / (2 – 2y)³
Therefore, the second derivative of y with respect to x is given by the expression 4 / (2 – 2y)³.
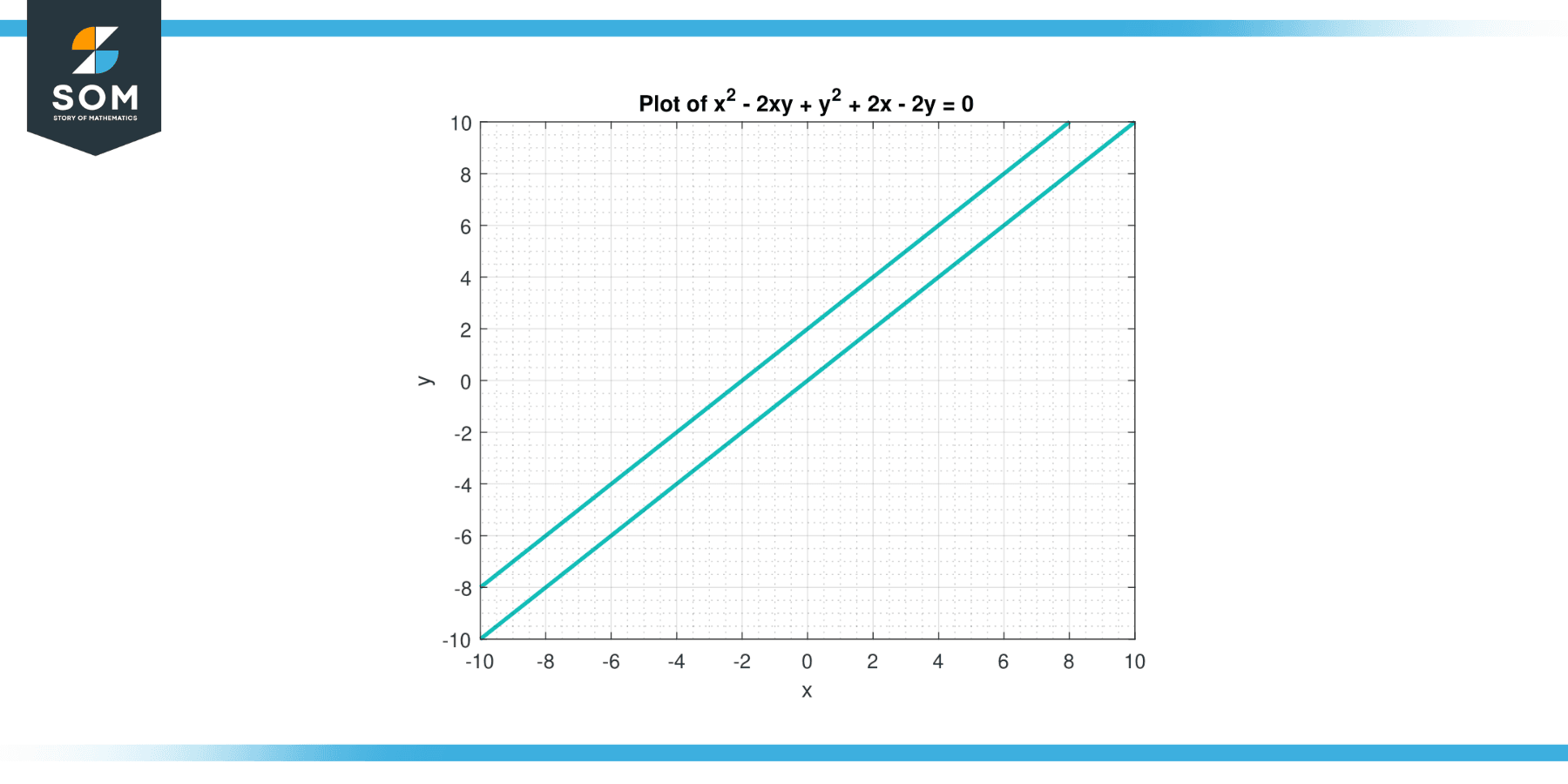
Figuer-3.
Example 4
Consider the equation x² + y³ = x³ + y². Find the second derivative of y with respect to x.
Solution
Differentiate the equation implicitly to find the first derivative:
2x + 3y² * dy/dx = 3x² + 2y * dy/dx
Rearranging, we get:
dy/dx = (3x² – 2x) / (3y² – 2y)
Now, differentiate the equation again to find the second derivative:
d²y/dx² = [(3y² – 2y) * (6x – 2) – (3x² – 2x) * (6y – 2)] / (3y² – 2y)²
Simplifying further, we obtain the expression:
d²y/dx² = (4 – 12xy + 8x²) / (3y² – 2y)²
Therefore, the second derivative of y with respect to x is given by the expression (4 – 12xy + 8x²) / (3y² – 2y)².
Example 5
Consider the equation x² + y² = 4. Find the second derivative of y with respect to x.
Solution
Differentiate the equation implicitly to find the first derivative:
2x + 2y * dy/dx = 0
Simplifying, we get:
dy/dx = -x/y
Now, differentiate the equation again to find the second derivative:
d²y/dx² = (y * d²y/dx² – dy/dx * x) / y²
Substituting dy/dx = -x/y, we have:
d²y/dx² = (y * d²y/dx² + x²/y) / y²
Simplifying further, we obtain the expression:
d²y/dx² = (x² + y²) / y³
Since the equation x² + y² = 4 is given, we substitute y² = 4 – x²:
d²y/dx² = (x² + (4 – x²)) / (4 – x²)^{3/2}
To simplify, we have the following:
d²y/dx² = 4 / $(4 – x²)^{3/2}$
Therefore, the second derivative of y with respect to x is given by the expression 4 / $(4 – x²)^{3/2}$.
Example 6
Consider the equation x³ + y³- 3xy = 0. Find the second derivative of y with respect to x.
Solution
Differentiate the equation implicitly to find the first derivative:
3x² + 3y² * dy/dx – 3(dy/dx) * y – 3x = 0
Simplifying, we get:
dy/dx = (x² – y²) / (y – x)
Now, differentiate the equation again to find the second derivative:
d²y/dx² = [(y – x) * (2x – 2y) – (x² – y²)] / (y – x)²
Simplifying further, we obtain the expression:
d²y/dx² = (y² – 4xy + x²) / (y – x)²
Therefore, the second derivative of y with respect to x is given by the expression (y² – 4xy + x²) / (y – x)².
Example 7
Consider the equation x² – 2xy +y² = 9. Find the second derivative of y with respect to x.
Solution
Differentiate the equation implicitly to find the first derivative:
2x – 2y – 2y * dy/dx + 2x – 2 * dy/dx = 0
Simplifying, we get:
dy/dx = (2x – 2y) / (2x – 2)
Now, differentiate the equation again to find the second derivative:
d²y/dx² = [(2x – 2) * (2 – 2 * dy/dx) – (2x – 2y) * (-2 * dy/dx)] / (2x – 2)²
Simplifying further, we obtain the expression:
d²y/dx² = 4 / (2x – 2)³
Therefore, the second derivative of y with respect to x is given by the expression 4 / (2x – 2)³.
Example 8
Consider the equation x² + 3xy + y² = 4. Find the second derivative of y with respect to x.
Solution
Differentiate the equation implicitly to find the first derivative:
2x + 3y * dy/dx + 3x * dy/dx + 2y = 0
Simplifying, we get:
dy/dx = (-2x – 2y) / (3x + 3y)
Now, differentiate the equation again to find the second derivative:
d²y/dx² = [(3x + 3y) * (-2 – 2 * dy/dx) – (-2x – 2y) * (3 + dy/dx)] / (3x + 3y)²
Simplifying further, we obtain the expression:
d²y/dx² = (6x² – 6xy + 6y² + 4x + 4y) / (3x + 3y)²
Therefore, the second derivative of y with respect to x is given by the expression (6x² – 6xy + 6y² + 4x + 4y) / (3x + 3y)².
All images were created with MATLAB.

