JUMP TO TOPIC

In this article, we delve into the world of inequalities, uncovering the essence of the reverse triangle inequality, its proof, its real-world implications, and its connections to the broader mathematical landscape.
Definition of Reverse Triangle Inequality
The reverse triangle inequality, also known as the negative triangle inequality, is a theorem in mathematics that relates to the lengths of the sides of a triangle, similar to the standard triangle inequality. However, instead of giving an upper bound for the sum of the lengths of two sides of a triangle, the reverse triangle inequality provides a lower bound.
The reverse triangle inequality states that for any real numbers a and b, the absolute difference of a and b is less than or equal to the absolute value of their sum. This can be mathematically represented as:
|a – b| ≤ |a + b|
Similarly, it can be expressed in the context of the lengths of the sides of a triangle. If a, b, and c are the lengths of the sides of a triangle, then:
|a – b| ≤ c ≤ a + b
The reverse triangle inequality provides a range within which the length of the third side of a triangle must fall, given the lengths of the other two sides.
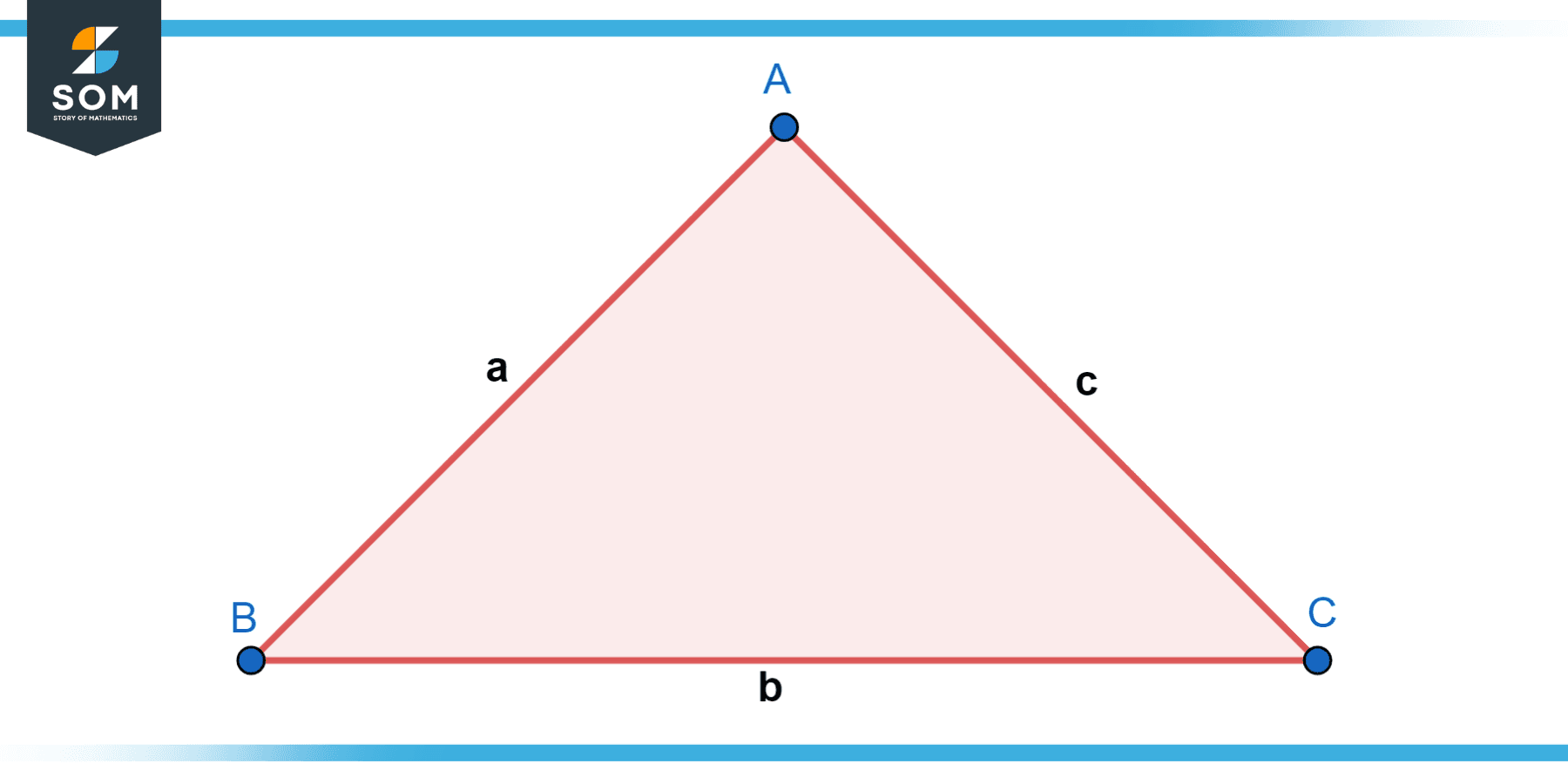
Figure-1.
Properties of Reverse Triangle Inequality
The reverse triangle inequality also referred to as the negative triangle inequality, has several interesting and crucial properties that make it vital in mathematics. The theorem, at its core, outlines the lower limit for the difference between two real numbers or two sides of a triangle. Below are some of the key properties of the reverse triangle inequality.
Absolute Differences
The reverse triangle inequality indicates that the absolute difference between any two real numbers or the lengths of two sides of a triangle is less than or equal to the absolute value of their sum. This rule is applicable to all real numbers and lengths, making it a universal law within its applicable contexts.
Establishing Boundaries
The theorem effectively establishes lower and upper boundaries for the possible lengths of a triangle’s sides. Given any two sides of a triangle, the reverse triangle inequality sets a range for the possible length of the third side.
The length of the third side should be greater than or equal to the absolute difference of the lengths of the other two sides and less than or equal to the sum of the lengths of the other two sides.
Handling Negative Numbers
An interesting aspect of the reverse triangle inequality is that it effectively manages negative numbers. By dealing with absolute values, it bypasses the ambiguity introduced by negative numbers. This is especially useful when working in mathematical fields where negative quantities have significant interpretations, such as in the case of vectors in physics.
Applicability
While its name suggests a relationship with geometric triangles, the reverse triangle inequality is broadly applicable in many other fields of mathematics and science. It plays a vital role in abstract algebra, analysis, probability, statistics, and computer science, especially in error analysis, quantifying uncertainty, and evaluating the efficiency of algorithms.
Relationship with Triangle Inequality
The reverse triangle inequality is a mirror image of the triangle inequality in the sense that while the triangle inequality gives the upper limit for the sum of the lengths of two sides of a triangle, the reverse triangle inequality provides the lower limit.
Exercise
Example 1
Let a = 4 and b = 3. According to the reverse triangle inequality:
|a – b| ≤ |a + b|
|4 – 3| ≤ |4 + 3|
1 ≤ 7
So, the reverse triangle inequality holds in this case.
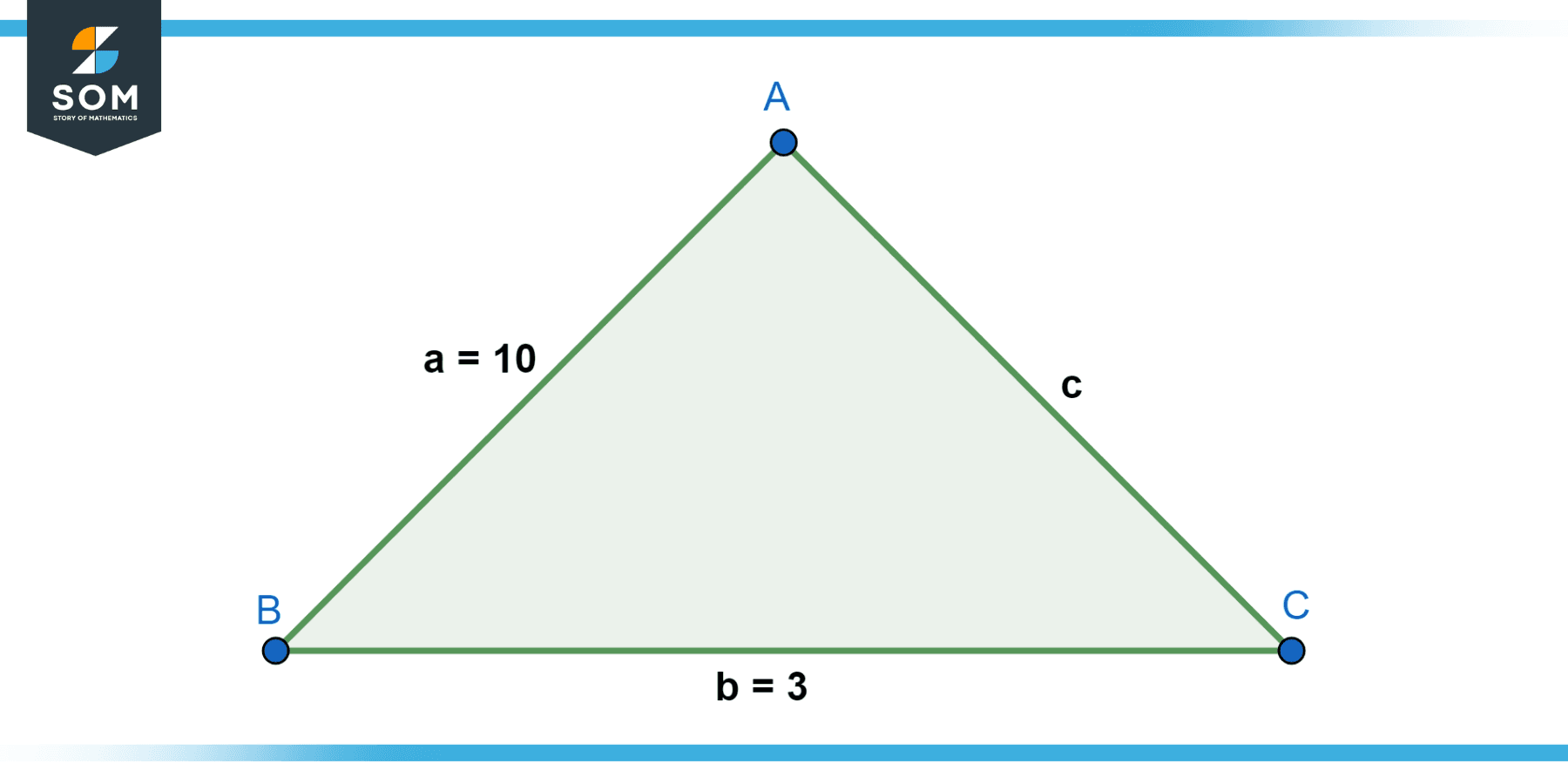
Figure-2.
Example 2
Let a = -2 and b = -2. Then:
|-2 – (-2)| ≤ |-2 + (-2)|
|0| ≤ |-4|
0 ≤ 4
This inequality is true.
Example 3
Let a = -3 and b = -7. Then:
|-3 – (-7)| ≤ |-3 + (-7)|
|4| ≤ |-10|
4 ≤ 10
This inequality is valid.
Example 4
Let a = 0 and b = 0. Then:
|0 – 0| ≤ |0 + 0|
0 ≤ 0
This inequality is true.
Example 5
Let a = 10 and b = 2. Then:
|10 – 2| ≤ |10 + 2|
8 ≤ 12
This inequality holds true.
Figure-3.
Applications
The reverse triangle inequality is a key principle in mathematics with a variety of applications across several disciplines. Here are a few notable applications in different fields:
Mathematics and Statistics
In these fields, the reverse triangle inequality is often used to establish boundaries for solutions to equations or inequalities. It is also employed to create confidence intervals in statistics when estimating population parameters based on sample data.
Computer Science
Algorithms, particularly those related to sorting, searching, and optimization, frequently use the reverse triangle inequality to help determine the most efficient paths or solutions. For instance, path-finding algorithms help to quickly exclude certain paths without detailed computations, thereby increasing the efficiency of the algorithm.
Physics
In physics, the reverse triangle inequality can be used in vector analysis, especially in establishing limits for resultant vectors. It also comes in handy when dealing with concepts such as uncertainty in measurements or distances between particles.
Engineering
Engineers often use the reverse triangle inequality to check the feasibility of a solution or to determine tolerances in various engineering disciplines. For example, in mechanical engineering, it can be used to calculate the maximum and minimum possible lengths of a mechanical part given certain tolerances.
Data Science and Machine Learning
In these areas, the reverse triangle inequality can be used for error estimation, bounding the difference between predicted and actual values. It is also useful in algorithms that deal with clustering, pattern recognition, and classification.
Economics and Finance
Economists and financial analysts utilize the reverse triangle inequality to bound uncertainties, calculate ranges for potential outcomes, and provide limits on error in economic and financial models.
All images were created with GeoGebra.
