JUMP TO TOPIC

In this article, we dive into the captivating world of a triangle inside a circle, unraveling the beautiful intricacies of this geometric arrangement. Join us as we navigate through a series of theorems, concepts, and real-world applications that illuminate the richness of this captivating geometric relationship.
Definition of Triangle Inside a Circle
A triangle inside a circle, often referred to as a circumscribed or inscribed triangle, is a triangle where all three vertices lie on the circumference of the circle. This circle is typically called the circumscribed circle or circumcircle of the triangle.
In a broader sense, the term can also refer to any triangle that fits entirely within a circle, whether or not its vertices touch the circle’s circumference. In such a case, the circle is the triangle’s incircle.
However, most commonly, when referring to a “triangle inside a circle,” we mean a triangle whose vertices are on the circle’s circumference.
Figure-1.
Properties of Triangle Inside a Circle
When discussing a triangle inside a circle, we typically refer to a triangle whose vertices lie on the circumference, also known as a circumscribed triangle. Here are some key properties and theorems associated with a circumscribed triangle:
Circumcircle
A triangle’s circumcircle is a circle that passes through all of the triangle’s vertices. The center of this circle is called the circumcenter.
Circumradius
The radius of the circumcircle is called the circumradius. It is the distance from the circumcenter to any of the triangle’s vertices. Importantly, all sides of the triangle subtend the same circumradius.
Circumcenter
The circumcenter of a triangle is the point where the perpendicular bisectors of the sides intersect. In an acute triangle, the circumcenter is inside the triangle; in a right triangle, it’s at the midpoint of the hypotenuse; in an obtuse triangle, it’s outside.
Circumcenters and Vertices form Equilateral Triangles
You form three smaller triangles if you join the circumcenter to the three vertices. These smaller triangles are all congruent, and their sides are all equal.
Central Angle Theorem
For any two points on the circle’s circumference, the angle subtended at the center is twice that at any point on the alternate arc.
Inscribed Angle Theorem
The angle subtended by an arc at the circumference is half the angle subtended by the same arc at the center. This property implies that every inscribed angle that subtends the same arc or intercepts the same segment is equal.
Law of Sines
The ratio of the length of a side of a triangle to the sine of the angle opposite that side is the same for all three sides and angles. This ratio is equal to the diameter of the triangle’s circumcircle.
Existence of Circumscribed Circle
Every triangle has one and only one circumscribed circle.
Understanding these properties can provide deep insights into the geometry and the algebraic relationships within a triangle and its circumcircle.
Ralevent Formulas
Several formulas are associated with triangles inside a circle (circumscribed triangles). Some of the most essential ones include:
Circumradius Formula
The formula for the circumradius (R) of a triangle with side lengths a, b, and c, and area (K) is:
R = (a * b * c) / (4 * K)
Triangle Area Formula (Heron’s formula)
If you know the lengths of the sides a, b, and c, then the area (K) of the triangle can be found using Heron’s formula:
s = (a + b + c) / 2 (semi-perimeter)
K = √(s * (s – a) * (s – b) * (s – c))
Law of Sines
For a triangle with sides of lengths a, b, and c opposite angles A, B, and C, respectively, and circumradius R, the law of sines states:
a/sin(A) = b/sin(B) = c/sin(C) = 2R
Central Angle
If a triangle is inscribed in a circle, the circle’s center is O, and the triangle’s vertices are A, B, and C, then ∠AOB is twice ∠ACB.
Inscribed Angle
∠ACB = 1/2 ∠AOB
Exercise
Example 1
A circle is inscribed in an equilateral triangle with a side length of 10 cm. Find the radius of the circle.
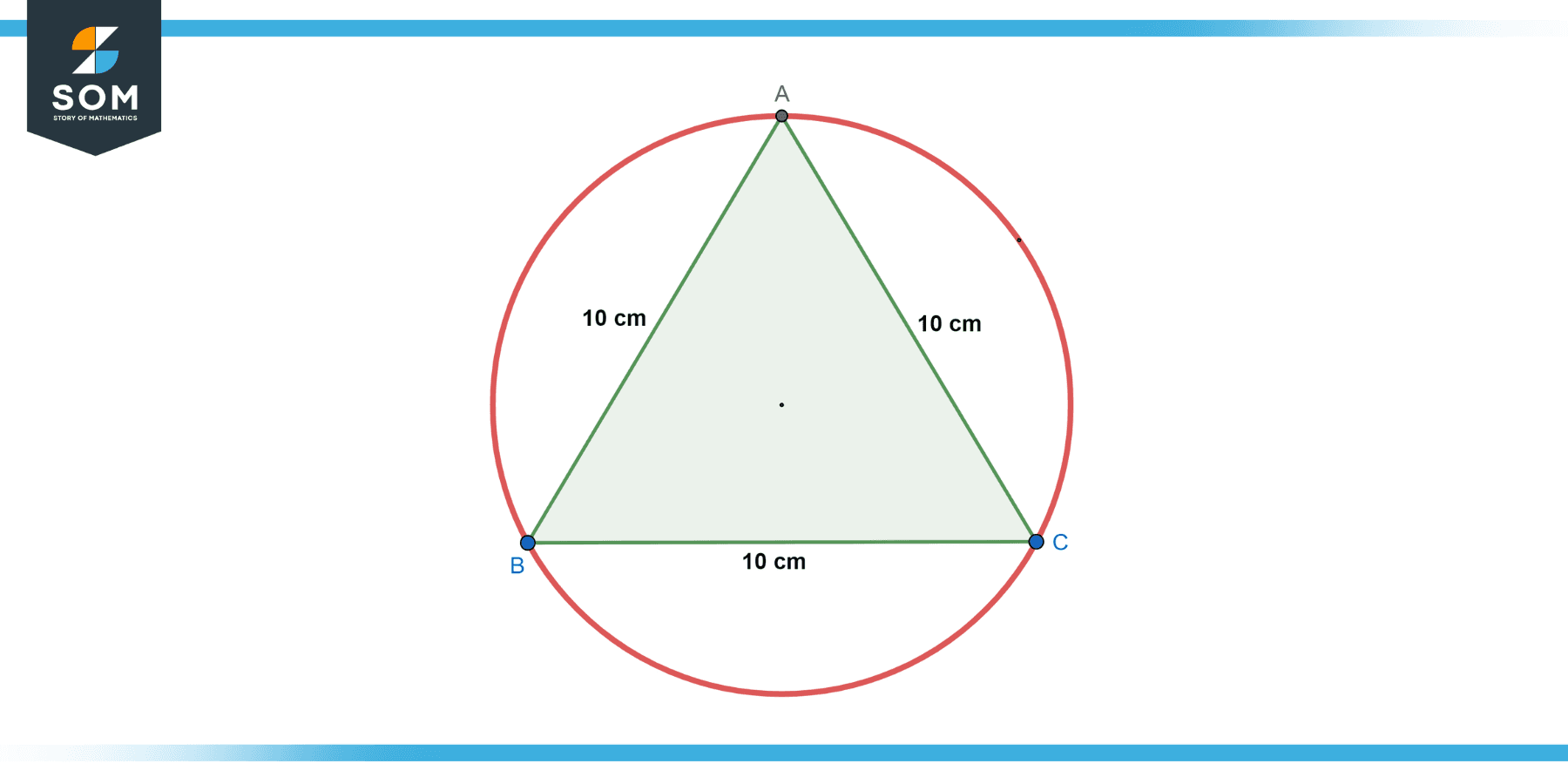
Figure-2.
Solution
For an equilateral triangle, the radius (r) of the inscribed circle is given by:
r = a * √3 / 6
where a is the side length of the triangle. So:
r = 10 * √3 / 6
r = 5 * √3/3 cm
Example 2
Given a circle with a radius of 10 cm, a triangle is inscribed such that all its sides are tangential to the circle. What is the area of the triangle?
Solution
The triangle is equilateral because all sides are equal in length (each being twice the radius of the inscribed circle). The area (A) of an equilateral triangle with side length (a) is given by:
A = (√3 / 4) * a²
Here a = 2 * 10 = 20 cm, so:
A = (√3 / 4) * (20)²
A = 100 * √3 cm²
Example 3
An isosceles triangle with a base of 12 cm and sides of 10 cm each is inscribed in a circle. Find the radius of the circle.
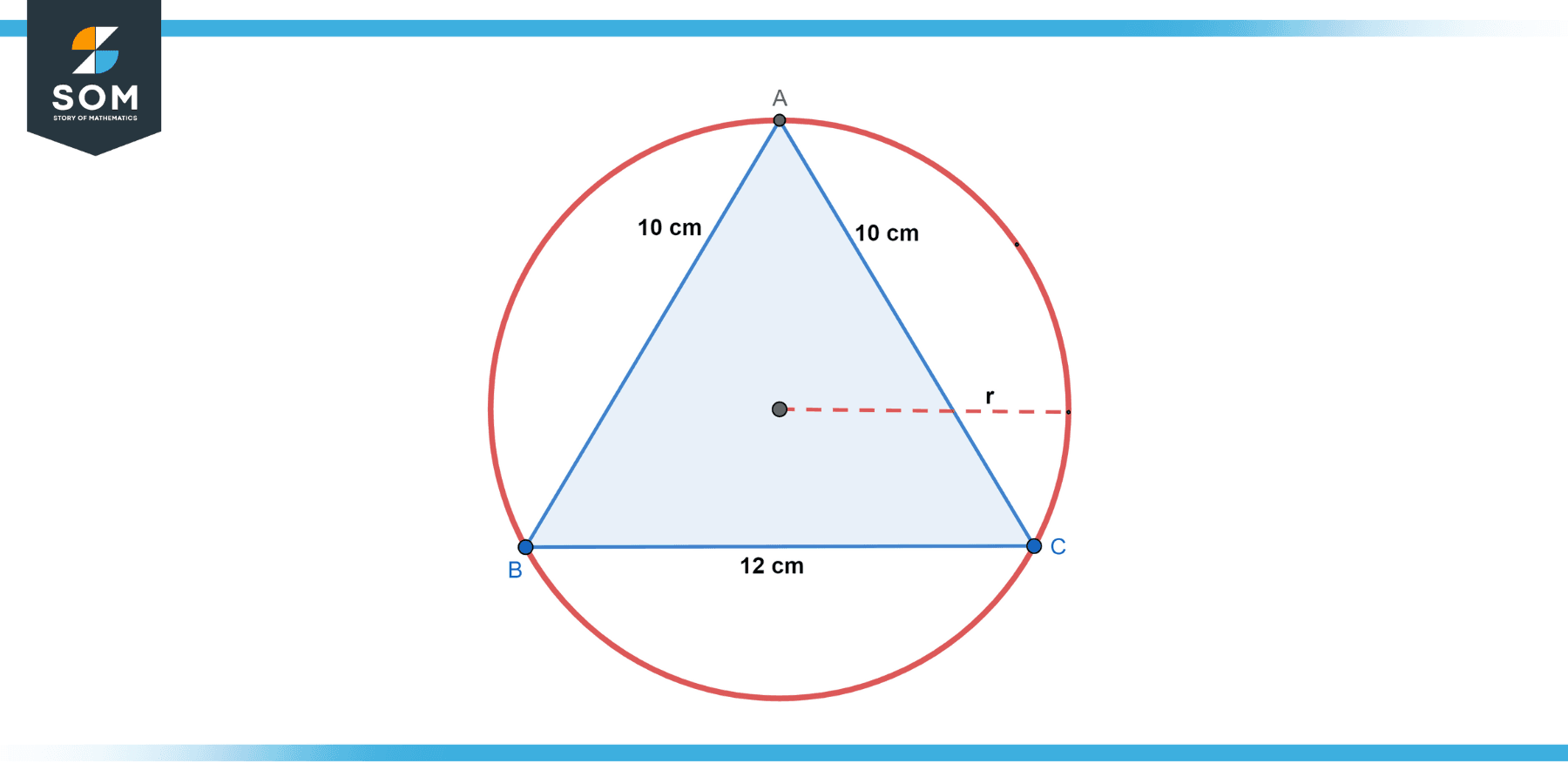
Figure-3.
Solution
We can find the height of the triangle using the Pythagorean theorem:
h = √[(10²) – (12/2)²]
h = √64
h = 8 cm
The circle’s diameter is the hypotenuse of the right triangle (which is the side of the isosceles triangle), so the circle’s radius is half of this:
10/2 = 5 cm
Example 4
A right triangle with sides of 6 cm, 8 cm, and 10 cm is inscribed in a circle. Find the radius of the circle.
Solution
In a right triangle, the hypotenuse is the diameter of the circumcircle. So, the circle’s radius is half the hypotenuse’s length:
r = 10/2
r = 5 cm
Example 5
Given an isosceles triangle inscribed in a circle with a radius of 5 cm and the base of the triangle being a diameter of the circle, find the area of the triangle.
Solution
Since the triangle’s base is the circle’s diameter, the triangle is a right triangle. A triangle’s area (A) is:
A = 1/2 * base * height
Here the base = 2 * radius = 10 cm, and the height = radius = 5 cm. So:
A = 1/2 * 10 * 5
A = 25 cm²
Example 6
A triangle is inscribed in a circle with a radius of 12 cm, and the sides of the triangle are 24 cm, 10 cm, and 26 cm. Show that this triangle is a right triangle.
Solution
We can use the Pythagorean theorem. If it is a right triangle, the square of the hypotenuse (the largest side) should equal the sum of the squares of the other two sides. Indeed:
26² = 24²+ 10²
676 = 576 + 100
Example 7
An equilateral triangle is inscribed in a circle with a radius of 10 cm. Find the side length of the triangle.
Solution
In an equilateral triangle inscribed in a circle, the side length (a) is given by:
a = 2 * r * √3
where r is the circle’s radius. So:
a = 2 * 10 * √3
a = 20 * √3 cm
Example 8
An isosceles triangle with a base of 14 cm and sides of length 10 cm each is inscribed in a circle. Find the radius of the circle.
Solution
First, find the height of the triangle using the Pythagorean theorem:
h = √[(10²) – (14/2)²]
h = √36
h = 6 cm
In this isosceles triangle, the hypotenuse of the right triangle (also the side of the triangle) is the circle’s diameter. So the circle’s radius is half of this:
r = 10/2
r = 5 cm
Applications
The concept of a triangle inside a circle (circumscribed triangle) has wide-ranging applications in various fields. Here are a few key examples:
Mathematics
Of course, the first application that comes to mind is in mathematics itself. The theorems and principles derived from the circumscribed triangle concept are fundamental to Euclidean geometry and trigonometry. For instance, the Law of Sines and the Inscribed Angle Theorem are crucial for solving angles and distances problems.
Physics
Physics often makes use of geometric principles in various subfields. For example, principles derived from circumscribed triangles can prove useful in studying circular motion and wave mechanics.
Engineering & Architecture
Engineers and architects often apply principles of geometry, including those of circumscribed triangles, in design and structural analysis. For example, the circular structures often seen in architecture and infrastructure, such as roundabouts or domes, often involve considerations of inscribed and circumscribed polygons.
Computer Graphics & Game Design
Many computer graphics algorithms rely on computational geometry, particularly those used in 3D modeling and game design. The concept of a circumscribed triangle can help in mesh generation and collision detection, essential aspects of 3D modeling and animation.
Astronomy
Astronomers often use geometric principles to calculate distances and angles between celestial bodies. Circumscribed triangles can help in calculating these distances based on observed angles.
Geography & Cartography
In these fields, the principles of geometric shapes like triangles and circles help measure distances, represent the Earth’s surface, and determine geographic positions.
Navigation & GPS Technology
The triangle inside a circle is a common symbol used in navigation and GPS technology to represent the user’s position and orientation. Here are some applications of the triangle inside a circle in this context:
Map Display
In navigation systems, the triangle inside a circle is often used to represent the user’s position on a map. The triangle indicates the direction the user faces, while the circle represents the range of accuracy or uncertainty in the position fix.
Waypoint Navigation
When navigating between waypoints, the triangle inside a circle can indicate the direction and distance to the next waypoint. The triangle points towards the waypoint, and the circle represents the user’s position accuracy.
Turn-by-Turn Directions
In GPS navigation systems, the triangle inside a circle is commonly used to provide turn-by-turn directions. The triangle indicates the user’s current position, and the circle represents the upcoming intersection or turn.
Compass Functionality
Some GPS devices and smartphone apps include a compass feature that utilizes the triangle inside a circle. The triangle points to the magnetic north, allowing users to determine their heading and navigate in a particular direction.
Augmented Reality Navigation
In augmented reality (AR) navigation applications, the triangle inside a circle can be overlaid on a live camera feed, providing real-time visualization of the user’s position and orientation. This lets users see virtual directions and guidance overlaid in the real world, enhancing their navigation experience.
Geocaching
Geocaching is a popular outdoor activity where participants use GPS coordinates to find hidden containers or “caches.” The triangle inside a circle is often displayed on GPS devices or smartphone apps to represent the user’s location and guide them to the cache.
Search and Rescue
The triangle inside a circle is also utilized in search and rescue operations. Rescuers can track their positions and coordinate with other team members using GPS technology, and the symbol helps them visualize their location relative to the search area or target.
These applications underline how seemingly abstract geometric concepts can be fundamental in practical, real-world situations.
Historical Significance
The study of triangles inscribed in circles and, more broadly, the intersection of geometric shapes is a fundamental aspect of Euclidean geometry, named after the ancient Greek mathematician Euclid.
His work, Elements, a 13-book series written around 300 BCE, includes the study of plane geometry, number theory, and the properties of geometric shapes, including the relationships between circles and triangles.
However, the exploration of triangles inside circles likely predates Euclid. The Greek philosopher Thales of Miletus, another Greek philosopher who lived in the 6th century BCE, is often credited with discovering Thales’ Theorem.
This theorem, dealing with inscribed angles in a semicircle (a specific instance of a triangle inscribed in a circle where one angle is a right angle), is one of the earliest recorded instances of this concept.
A notable development in this area is the discovery of Heron’s formula for finding the area of a triangle using the lengths of its sides. This formula is instrumental in deriving the circumradius of a triangle, which ties the study of triangles to circles. Heron of Alexandria, a Greek engineer, and mathematician, provided this formula in the first century CE.
Later, Indian mathematicians such as Aryabhata and Brahmagupta significantly contributed to studying circles and triangles. The work of these and other mathematicians formed the basis for the modern geometric understanding of circles and triangles and their intersections.
In the Middle Ages, Islamic scholars preserved and expanded on Greek and Indian mathematical traditions. They further studied the properties of circles and triangles, among other geometric shapes.
In the early modern period, the development of non-Euclidean geometries expanded the theoretical context in which triangles inscribed in circles could be studied, leading to our rich and diverse mathematical landscape.
All images were created with GeoGebra.
