
This article will focus on an intriguing task – finding the derivative of ln(2x) (the natural logarithm function). As one of the cornerstone concepts in calculus, the derivative serves as a powerful tool in deciphering the rate of change or the slope of a function at any point.
Defining Derivative of ln(2x)
The derivative of a function measures how the function changes as its input changes. It’s often described as the function’s “rate of change” or the slope of the tangent line to the function’s graph at a specific point.
The derivative of ln(2x), written as d/dx[ln(2x)], can be found by applying the chain rule, a basic theorem in calculus. The chain rule states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function multiplied by the derivative of the inner function.
The derivative of the natural logarithm function ln(x) is 1/x. And the derivative of 2x with respect to x is 2.
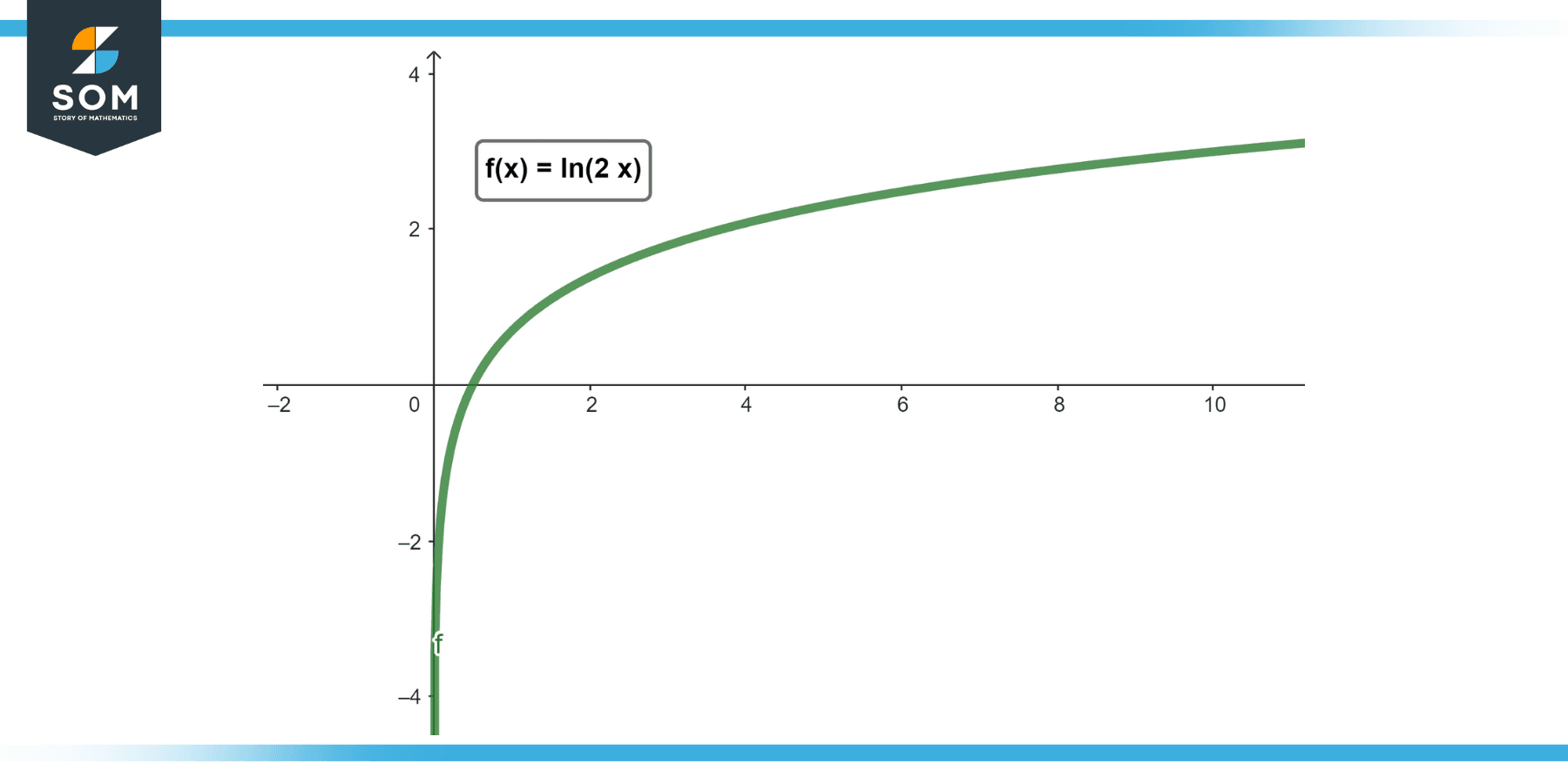
Figure-1.
Therefore, by the chain rule, the derivative of ln(2x) is:
d/dx[ln(2x)] = (1/(2x)) * 2
d/dx[ln(2x)] = 1/x
So, the derivative of ln(2x) is 1/x.
Properties of Derivative of ln(2x)
The derivative of ln(2x) is 1/x. This derivative has some key properties that are characteristic of derivative functions in general:
Linearity
The derivative operator is linear. This means that if you have two functions u(x) and v(x), the derivative of their sum is the sum of their derivatives. However, as ln(2x) is a single function, this property is not explicitly reflected here.
Local Information
The derivative of a function at a particular point gives the slope of the tangent line to the graph of the function at that point. For the function ln(2x), its derivative 1/x is the slope of the tangent line to the graph of ln(2x) at any point x.
Rate of Change
The derivative of a function at a certain point gives the rate of change of the function at that point. For the function ln(2x), its derivative 1/x represents how fast ln(2x) is changing at any point x.
Non-negativity for x > 0
The derivative 1/x is always positive for x > 0, which means that the function ln(2x) is increasing for x > 0. The greater the x, the slower the rate of increase (since 1/x gets smaller as x gets larger).
Undefined at x = 0
The derivative 1/x is undefined at x = 0, reflecting the fact that the function ln(2x) itself is undefined at x = 0.
Negativity for x < 0
The derivative 1/x is always negative for x < 0, which means that the function ln(2x) is decreasing for x < 0. However, since the natural logarithm of a negative number is undefined in the real number system, this is typically not relevant in most real-world applications.
Continuity and Differentiability
The derivative 1/x is continuous and differentiable for all x ≠ 0. This means that the function ln(2x) has a derivative at all such points, which informs us about the behavior and properties of the original function.
Exercise
Example 1
Compute d/dx[ln(2x)]
Solution
The derivative of ln(2x) is 1/x.
Example 2
Determine d/dx[2*ln(2x)]
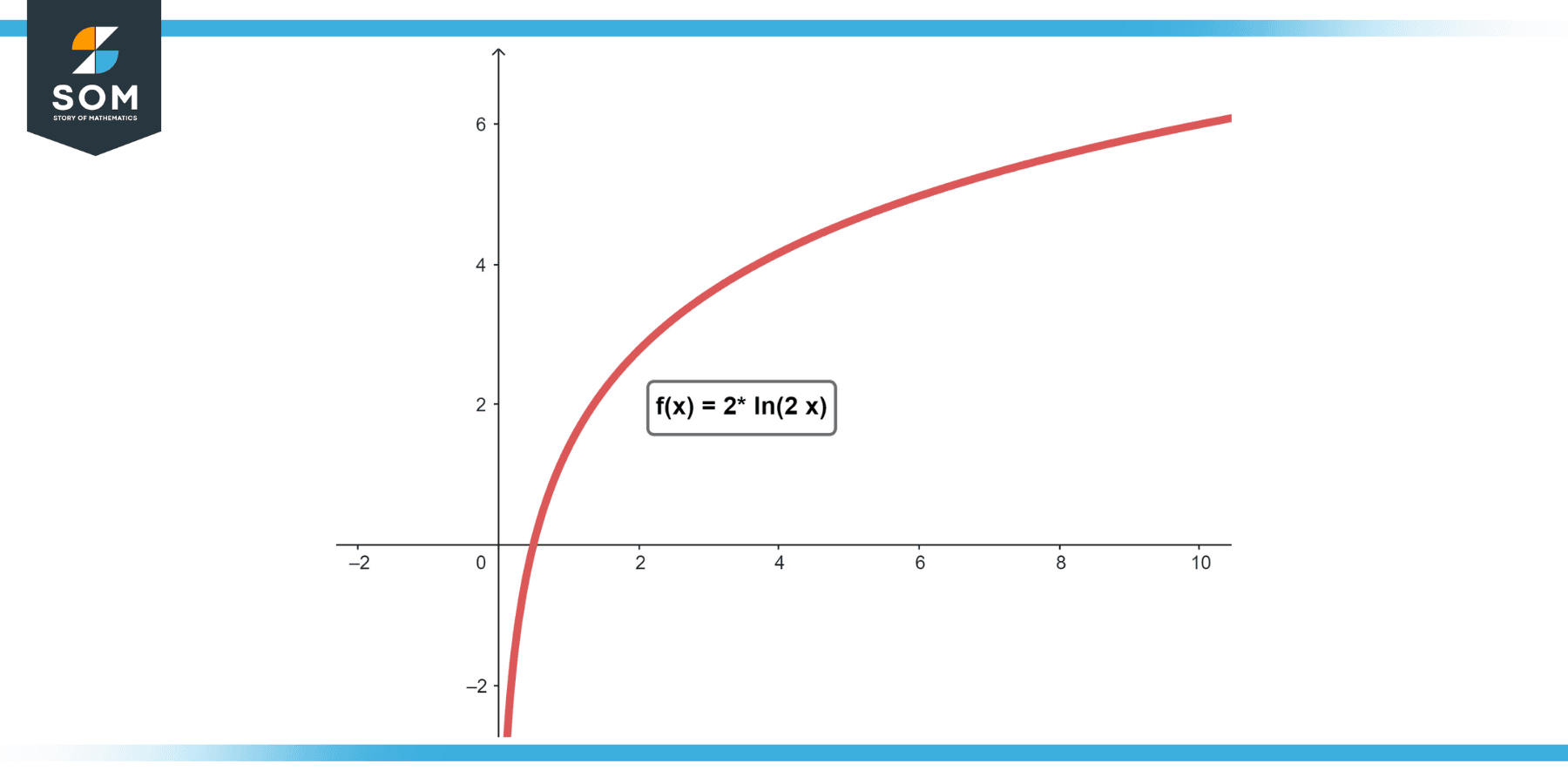
Figure-2.
Solution
Here, we use the rule that the derivative of a constant times a function is the constant times the derivative of the function. So, the derivative is:
2*(1/x) = 2/x
Example 3
Compute $d/dx[ln(2x)]^2$
Solution
We use the chain rule, which gives:
2ln(2x)(1/x) = 2ln(2x)/x
Example 4
Determine d/dx[ln(2x + 1)]
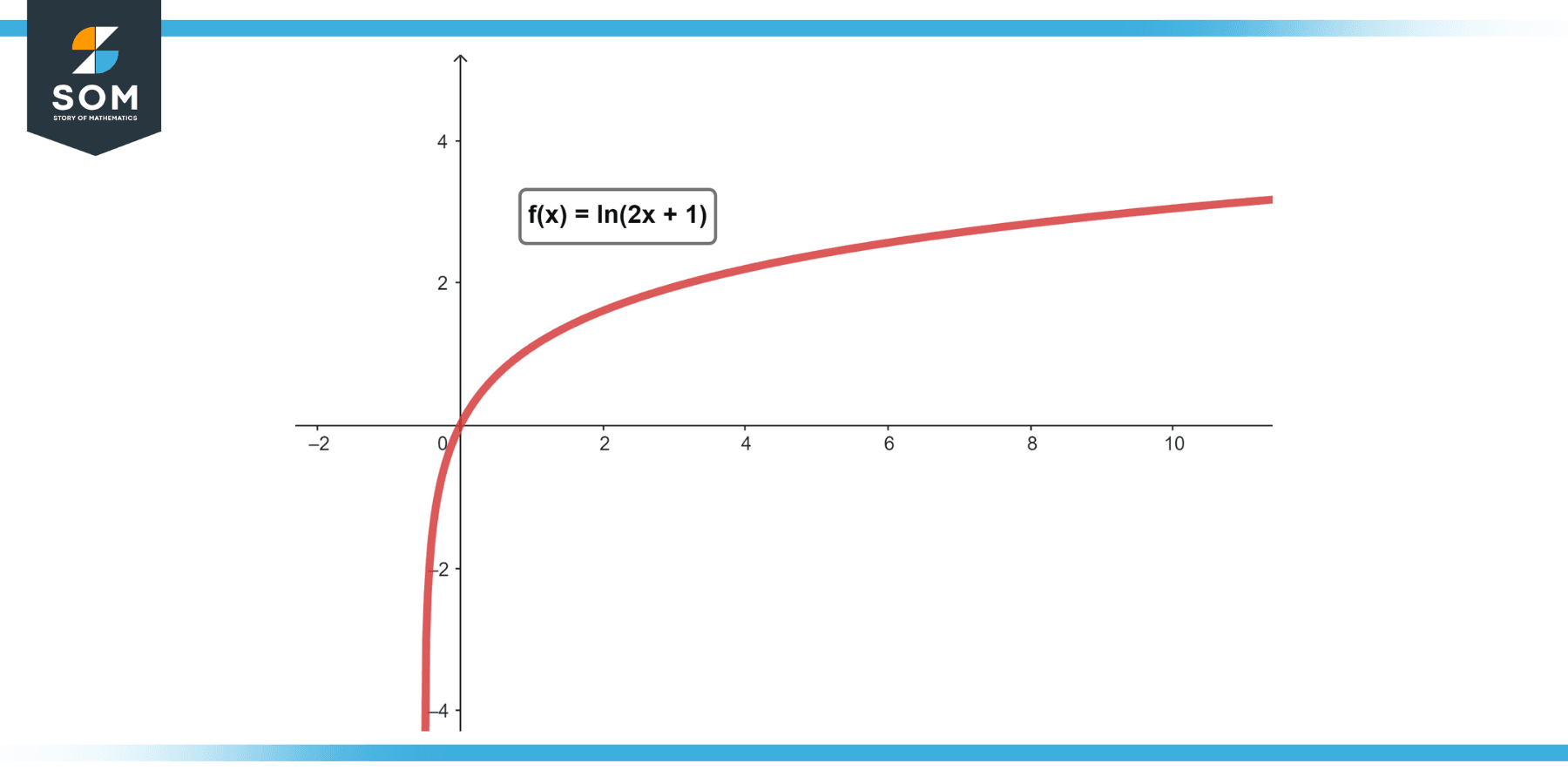
Figure-3.
Solution
Here, the derivative is:
1/(2x + 1) * 2 = 2/(2x + 1)
Example 5
Compute d/dx[ln(2x²)]
Solution
In this case, the derivative is:
1/(2x²) * 4x = 2/x
Example 6
Compute d/dx[3ln(2x) – 2]
Here, the derivative is:
3*(1/x) = 3/x
Example 7
Evaluate d/dx[ln(2x) / x]

Figure-4.
Solution
Here we have a quotient, so we use the quotient rule for differentiation (d/dx [u/v] = (vu’ – uv’) / v²), where u = ln(2x) and v = x.
The derivative is then:
(x*(1/x) – ln(2x)*1) / x² = (1 – ln(2x)) / x
Example 8
Determine d/dx[5ln(2x) + 3x²]
Solution
In this case, the derivative is:
5*(1/x) + 6x = 5/x + 6x
Applications
The derivative of ln(2x), which is 1/x, has broad applications across a variety of fields. Let’s explore some of these:
Physics
In physics, the concept of a derivative is fundamentally used to calculate rates of change. This concept finds wide application in various areas, such as motion studies where it helps determine velocity and acceleration. By taking derivatives of displacement with respect to time, we can obtain the instantaneous velocity and acceleration of an object.
Economics
In economics, the derivative of ln(2x) might be used in models where a natural logarithm is used to represent a utility function or production function. The derivative would then provide information about the marginal utility or marginal product.
Biology
In the study of population dynamics, the natural logarithm function often arises when examining exponential growth or decay (as in population growth or decay of biological specimens). The derivative, thus, helps in understanding the rate of change of the population.
Engineering
In electrical engineering, the natural logarithm and its derivative might be used in solving problems related to signal processing or control systems. Similarly, in civil engineering, it can be used in the analysis of stress-strain behavior of certain materials.
Computer Science
In computer science, particularly in machine learning and optimization algorithms, derivatives, including those of natural logarithms, are used to minimize or maximize objective functions, such as in gradient descent.
Mathematics
Of course, in mathematics itself, the derivative of ln(2x) and similar functions are frequently used in calculus in topics such as curve sketching, optimization problems, and differential equations.
All images were created with GeoGebra.
