JUMP TO TOPIC

The right triangle, a cornerstone of geometry, is a geometric shape that embodies both simplicity and mathematical significance. With its distinctive form defined by one right angle, the right triangle holds a special place in various fields, including mathematics, physics, engineering, and architecture. Its elegant proportions and inherent properties make it a fundamental building block for constructing complex structures and solving intricate problems.
We set off on a tour into the fascinating world of the right triangle in this essay, exploring its unique characteristics, fundamental principles, Pythagorean theorem, and practical applications. By unraveling the secrets of this geometric marvel, we aim to shed light on the profound impact of right triangles in shaping the foundations of theoretical knowledge and real-world structures.
Definition
A right triangle is a geometric shape that is defined by its specific properties. It is a triangle that contains one right angle, which measures 90 degrees. The right angle is formed by the intersection of two sides, known as the legs, and it is always opposite the longest side of the triangle, called the hypotenuse.
The other two angles in a right triangle are acute, or less than 90 degrees. The two sharp angles in a right triangle must add up to 90 degrees since the total angle in any triangle is always 180 degrees. Below is the generic diagram for a right triangle.
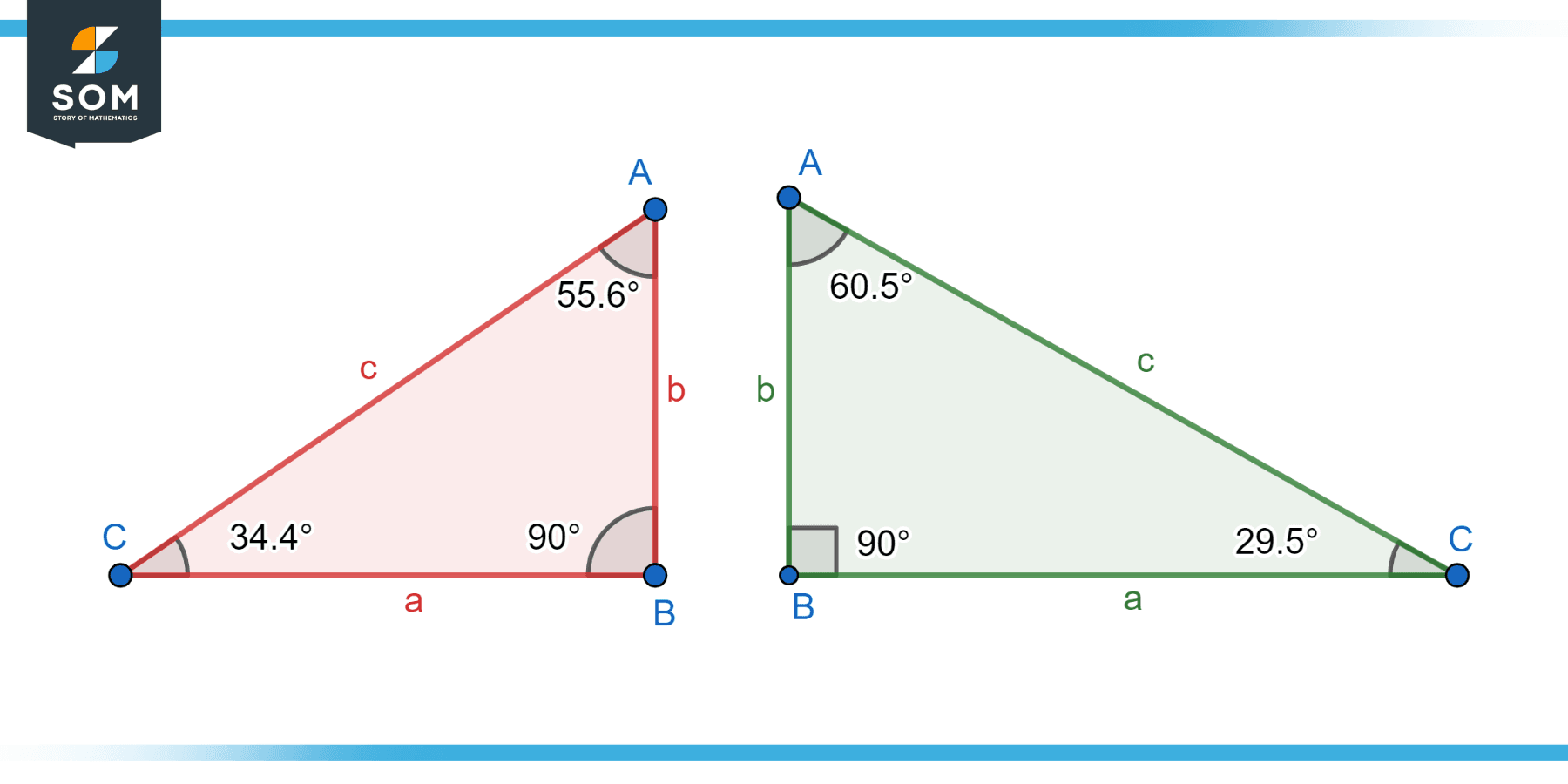
Figure-1: Generic right triangle.
The Pythagorean theorem is one of the basic concepts related to right triangles. The square of the lengths of the two legs in a right triangle must equal the square of the length of the hypotenuse, according to this theorem. This can be mathematically represented as $c^2 = a^2 + b^2$, “c” being the length of the hypotenuse and “a” and “b” being the lengths of the legs.
Historical Significance
The historical background of the right triangle, a geometric shape, dates back to ancient cultures and was crucial in the growth of mathematics and several scientific fields. The concept of the right triangle can be traced back to Ancient Mesopotamia and Ancient Egypt, where early civilizations recognized its special properties and utilized it in their architectural and surveying practices. The Egyptians, in particular, were skilled in geometry and used right triangles in their construction projects, such as the pyramids.
The study of right triangles flourished in Ancient Greece, with renowned mathematicians such as Pythagoras making significant contributions. Pythagoras’ Theorem states that the hypotenuse’s square is equal to the sum of its two other sides’ squares. according to Pythagoras’ Theorem. became a fundamental principle in geometry and trigonometry. The theorem is named after Pythagoras, but similar ideas were known in other ancient cultures as well.
During the Islamic Golden Age (8th to 14th centuries), scholars like Al-Khwarizmi and Ibn al-Haytham further expanded their knowledge of right triangles and their properties. They contributed to advancements in trigonometry, introducing new concepts and techniques for solving problems involving right triangles.
In Renaissance Europe, mathematicians and astronomers such as Leonardo da Vinci, Johannes Kepler, and Galileo Galilei relied on right triangles and trigonometry to explore the principles of optics, planetary motion, and perspective in art.
The study of right triangles continued to progress through the Enlightenment and into the modern era, with the development of trigonometric functions and their applications in various scientific and engineering fields.
Today, the understanding of right triangles and their properties is an essential part of mathematics education. Right triangles find extensive use in fields such as engineering, physics, navigation, computer graphics, and surveying. Trigonometry, which heavily relies on right triangles, provides a comprehensive framework for analyzing and solving problems involving angles, distances, and relationships between sides.
Fundamental Properties
Certainly! Here are the properties of the right triangle, a geometric shape, explained in detail:
Right Angle
The most distinguishing property of a right triangle is the presence of a right angle. A right angle measures 90 degrees and is formed where two sides of the triangle meet to create a perpendicular intersection.
Hypotenuse
In a right triangle, the hypotenuse is the side that faces the right angle. It is the longest side of the triangle and is denoted by the letter c. The hypotenuse is directly across from the right angle and forms the base for many important relationships in right triangles.
Legs
The other two sides of the right triangle, which are adjacent to the right angle, are called the legs. They are denoted by the letters a and b. The lengths of the legs can vary and are crucial for calculating other properties of the triangle.
Pythagorean Theorem
One of the fundamental properties of a right triangle is the Pythagorean theorem, named after the Greek mathematician Pythagoras.The square of the hypotenuse is equal to the sum of the squares of the two legs, according to this rule. In equation form, it is written as c² = a² + b².
Special Right Triangles
Right triangles can have specific ratios between their side lengths, resulting in special right triangles. The two most common special right triangles are the 45-45-90 triangle and the 30-60-90 triangle. In a 45-45-90 triangle, the two legs are congruent, and the hypotenuse is equal to the length of a leg multiplied by √2. In a 30-60-90 triangle, the lengths of the sides follow a specific ratio: the length of the shorter leg is half the length of the hypotenuse, and the length of the longer leg is √3 times the length of the shorter leg.
Trigonometric Functions
In a 45-45-90 triangle, the two legs are congruent, and the hypotenuse is equal to the length of a leg multiplied by √2. In a 30-60-90 triangle, the lengths of the sides follow a specific ratio: the length of the shorter leg is half the length of the hypotenuse, and the length of the longer leg is √3 times the length of the shorter leg.
Congruence and Similarity
Right triangles can be used to determine whether two triangles are congruent (having identical side lengths and angles) or similar (having proportional side lengths and congruent angles).
Understanding these properties of the right triangle allows for a comprehensive exploration of its geometry, relationships between sides and angles, and practical applications. Right triangles and their properties serve as the basis for trigonometry, navigation, engineering, and countless other fields where accurate calculations involving angles and distances are required.
Related Formulas
Below are the related formulas of the right triangle, explained in detail:
Pythagorean Theorem
One of the most important formulas for right triangles is the Pythagorean theorem. The hypotenuse is the side that forms the right angle, and the rule says that the square of its length is equal to the sum of the squares of the lengths of the other two sides. In equation form, it is written as c² = a² + b², where a and b are the lengths of the two legs, and c is the hypotenuse length.
Trigonometric Functions
Trigonometric functions are widely used in right triangles to relate the ratios of the side lengths to the angles within the triangle. The three primary trigonometric functions are:
Sine (sin)
The sine of an angle in a right triangle is the proportion of the length of the side directly across from the angle to the length of the hypotenuse.It is written as sin(A) = opposite / hypotenuse.
Cosine (cos)
The ratio of the neighboring side’s length to the hypotenuse’s length is known as the cosine of an angle in a right triangle. It is written as cos(A) = adjacent / hypotenuse.
Tangent (tan)
In a right triangle, the lengths of the adjacent and opposing sides are compared to determine the angle’s tangent. It is written as tan(A) = opposite/adjacent.
Special Right Triangle Formulas
Special right triangles, such as the 45-45-90 triangle and the 30-60-90 triangle, have specific formulas that relate to their side lengths. In a 45-45-90 triangle, the lengths of the two legs are equal, and the length of the hypotenuse is equal to the length of a leg multiplied by √2. In a 30-60-90 triangle, the lengths of the sides follow a specific ratio: the length of the shorter leg is half the length of the hypotenuse, and the greater leg is about √3 times longer than the shorter leg.
Area Formula
The formula to calculate the area of a right triangle is A = 0.5 × base × height, where the base and height are the lengths of the two legs. The base and height can be any two sides of the triangle as long as they form a right angle.
Perimeter Formula
The total length of all the sides makes up a right triangle’s perimeter. In a right triangle, the perimeter can be calculated by adding the lengths of the two legs and the hypotenuse: P = a + b + c.
Types
There are three main types of right triangles based on the relationships between their sides and angles. Let’s explore each type in detail:
Acute Right Triangle
An acute right triangle is a right triangle where both of the acute angles (the angles that are less than 90 degrees) are less than 45 degrees. In this type of triangle, the two legs are of different lengths, and the hypotenuse is the longest side. The Pythagorean theorem applies to acute right triangles, where c² = a² + b². The acute right triangle is characterized by its sharp angles and is commonly encountered in mathematical problems and applications. Below is the diagram for an acute right triangle.
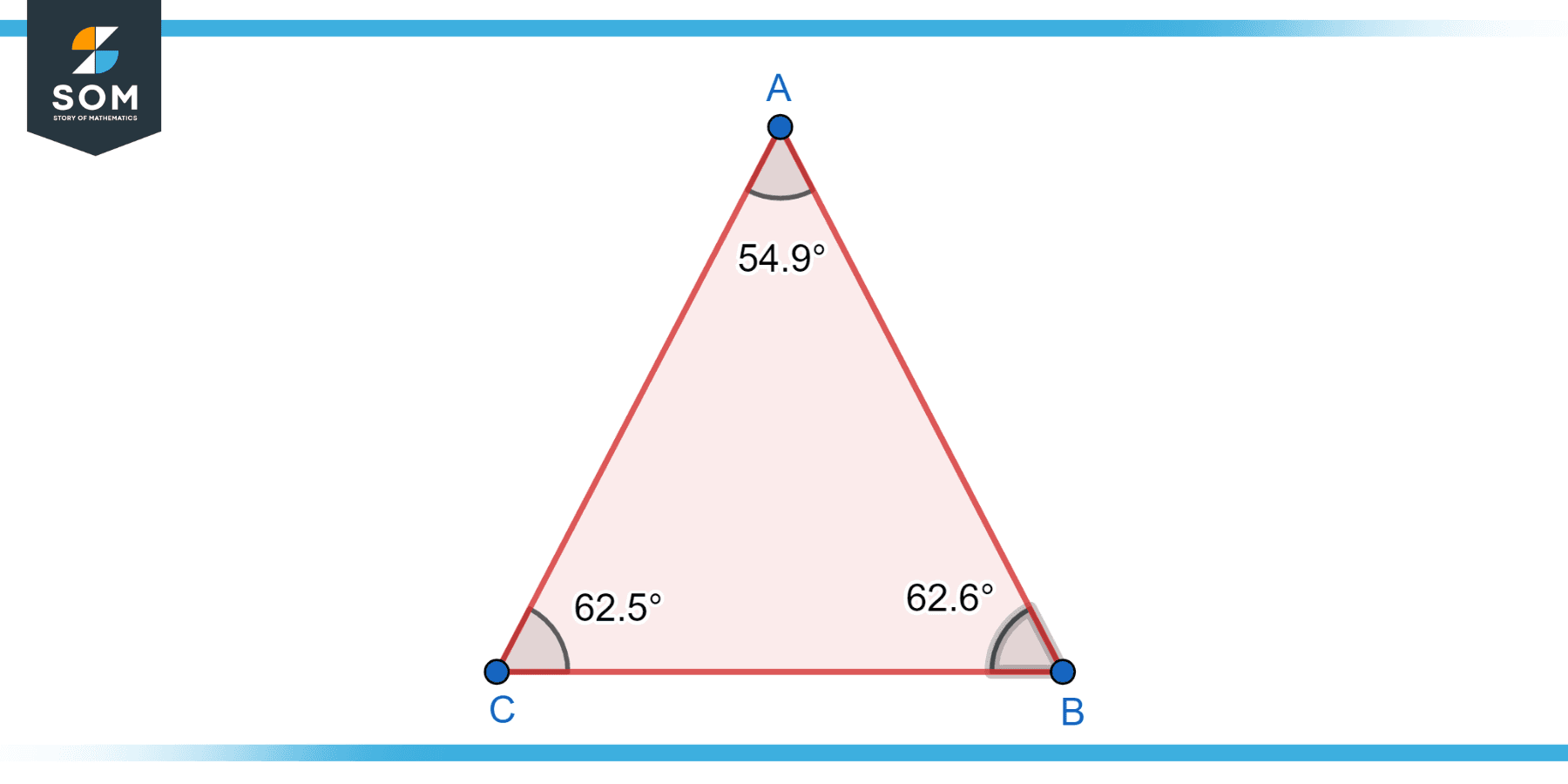
Figure-2: Acute right triangle.
Obtuse Right Triangle
An obtuse right triangle is a right triangle where one of the acute angles is greater than 45 degrees. The other acute angle remains less than 45 degrees, and the right angle is always 90 degrees. In an obtuse right triangle, the longest side is the one opposite the obtuse angle. The Pythagorean theorem also applies to obtuse right triangles, following the same formula as the acute right triangle. These triangles possess one larger angle, which gives them a distinct shape and characteristic. Below is the diagram for an obtuse right triangle.
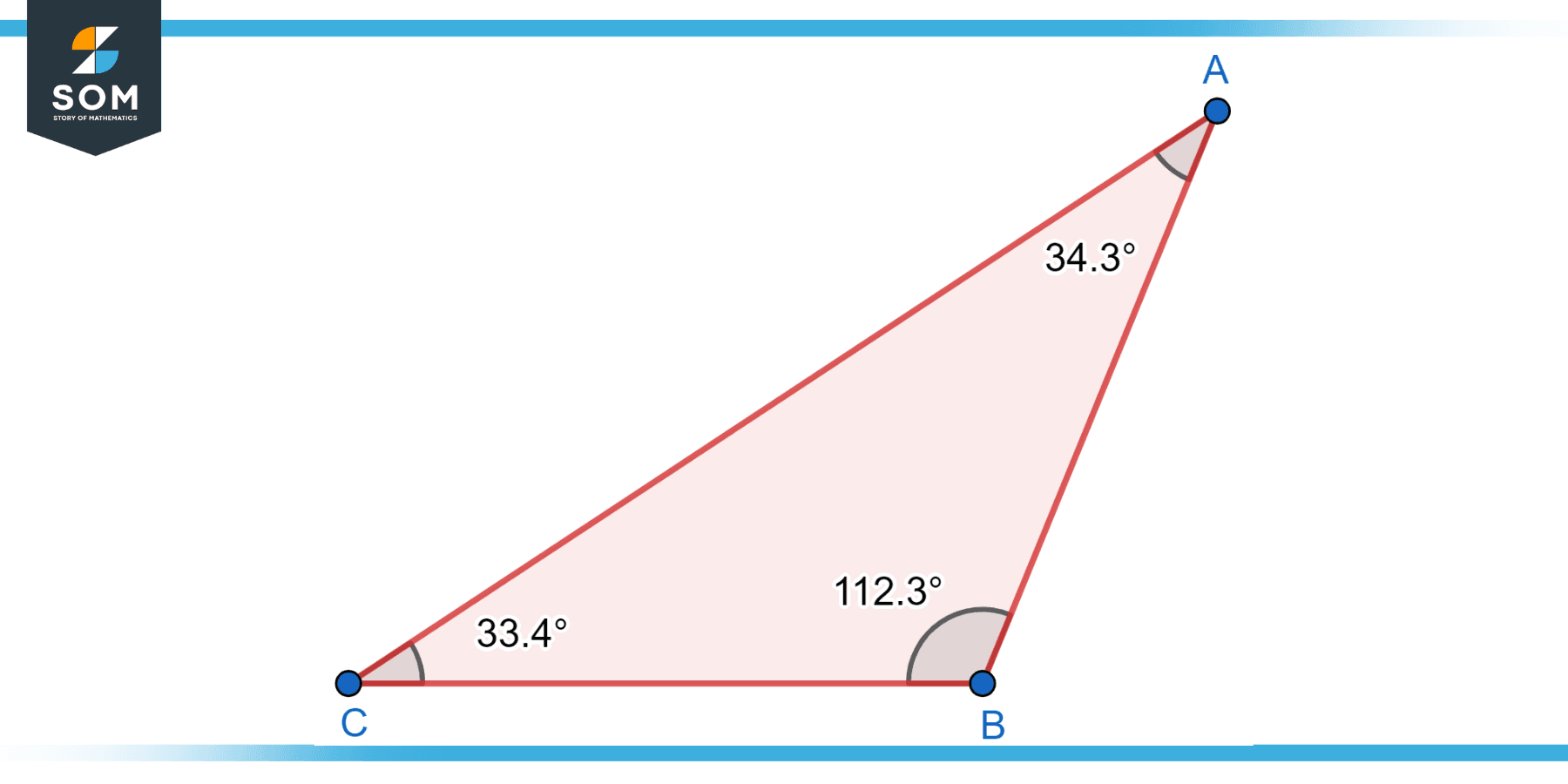
Figure-3: Obtuse right triangle.
Isosceles Right Triangle
An isosceles right triangle is a right triangle where two of the sides, the legs, are of equal length. The remaining side, the hypotenuse, is always longer than the legs. In an isosceles right triangle, both of the acute angles are 45 degrees. The Pythagorean theorem is simplified for isosceles right triangles as c² = 2a², where “a” denotes the length of the legs and “c” the length of the hypotenuse. Isosceles right triangles exhibit symmetry and are often used in geometric constructions and calculations. Below is the diagram for an isosceles right triangle.
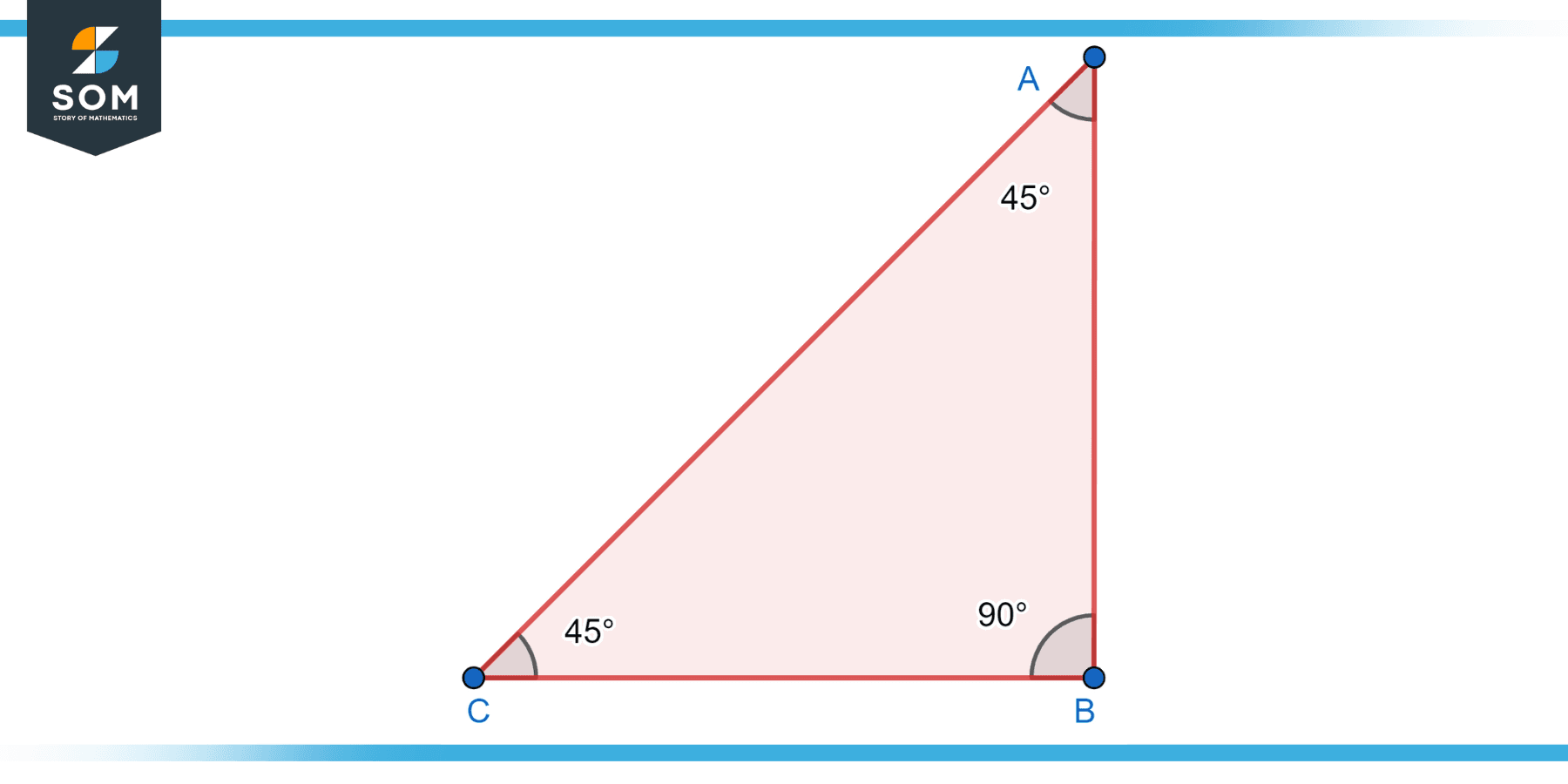
Figure-4: Isosceles right triangle.
Understanding the types of right triangles is important as it provides insights into their specific characteristics and properties. These types allow for a classification of right triangles based on their angle measures and side lengths, enabling more precise analysis and problem-solving in various mathematical and practical contexts.
Applications
Engineering
Right triangles are prevalent in engineering disciplines. They are utilized in structural design, architecture, and civil engineering for calculating forces, determining stability, and analyzing structural elements. Right triangles are also essential in fields like electrical engineering and circuit design, where they aid in calculating voltage, resistance, and impedance in complex circuits.
Physics
Right triangles find applications in physics for various calculations involving forces, vectors, and motion. In mechanics, right triangles are used to resolve forces into components and calculate their magnitudes and directions. Additionally, right triangles are employed in trigonometric calculations related to projectile motion, circular motion, and waves.
Surveying and Navigation
Right triangles play a significant role in surveying and navigation. Triangulation methods, which rely on the principles of right triangles, are used to determine distances, angles, and positions of points on the Earth’s surface. This is crucial in activities such as land surveying, mapmaking, and global positioning systems (GPS) technology.
Architecture and Construction
Right triangles are essential in architectural design and construction. They aid in creating geometrically balanced structures, determining angles for roof pitches, calculating stair dimensions, and ensuring proper alignments and measurements.
Astronomy
Right triangles are utilized in celestial navigation and astronomical calculations. Triangulation methods involving right triangles help determine the positions of celestial objects, measure distances in space, and navigate using celestial coordinates.
Art and Design
Right triangles are employed in art and design compositions to create balanced and aesthetically pleasing arrangements. The principles of right triangles help in achieving visual harmony, proportion, and perspective.
Understanding the applications of the right triangle in various fields provides insights into its practical significance and demonstrates its universal utility in different domains.
Exercise
Example 1
Find the length of the hypotenuse in a right triangle with legs measuring 3 units and 4 units.
Solution
Given: Length of leg a = 3 units Length of leg b = 4 units
We can apply the Pythagorean theorem to determine the length of the hypotenuse: c² = a² + b².
Substituting the given values:
c² = 3² + 4²
c² = 9 + 16
c² = 25
When we square the two sides, we discover:
c = √25
c = 5 units
Therefore, the length of the hypotenuse in the right triangle is 5 units.
Example 2
Determine the length of a leg in a right triangle with a hypotenuse of 10 units and the other leg measuring 6 units.
Solution
Given: Length of hypotenuse c = 10 units Length of one leg a = 6 units
To find the length of the other leg, b, we can use the Pythagorean theorem: c² = a² + b².
Substituting the given values:
10² = 6² + b²
100 = 36 + b²
b² = 100 – 36
b² = 64
When we square the two sides, we discover:
b = √64
b = 8 units
Therefore, the length of the other leg in the right triangle is 8 units.
Example 3
Calculate the area of a right triangle given in Figure-5.
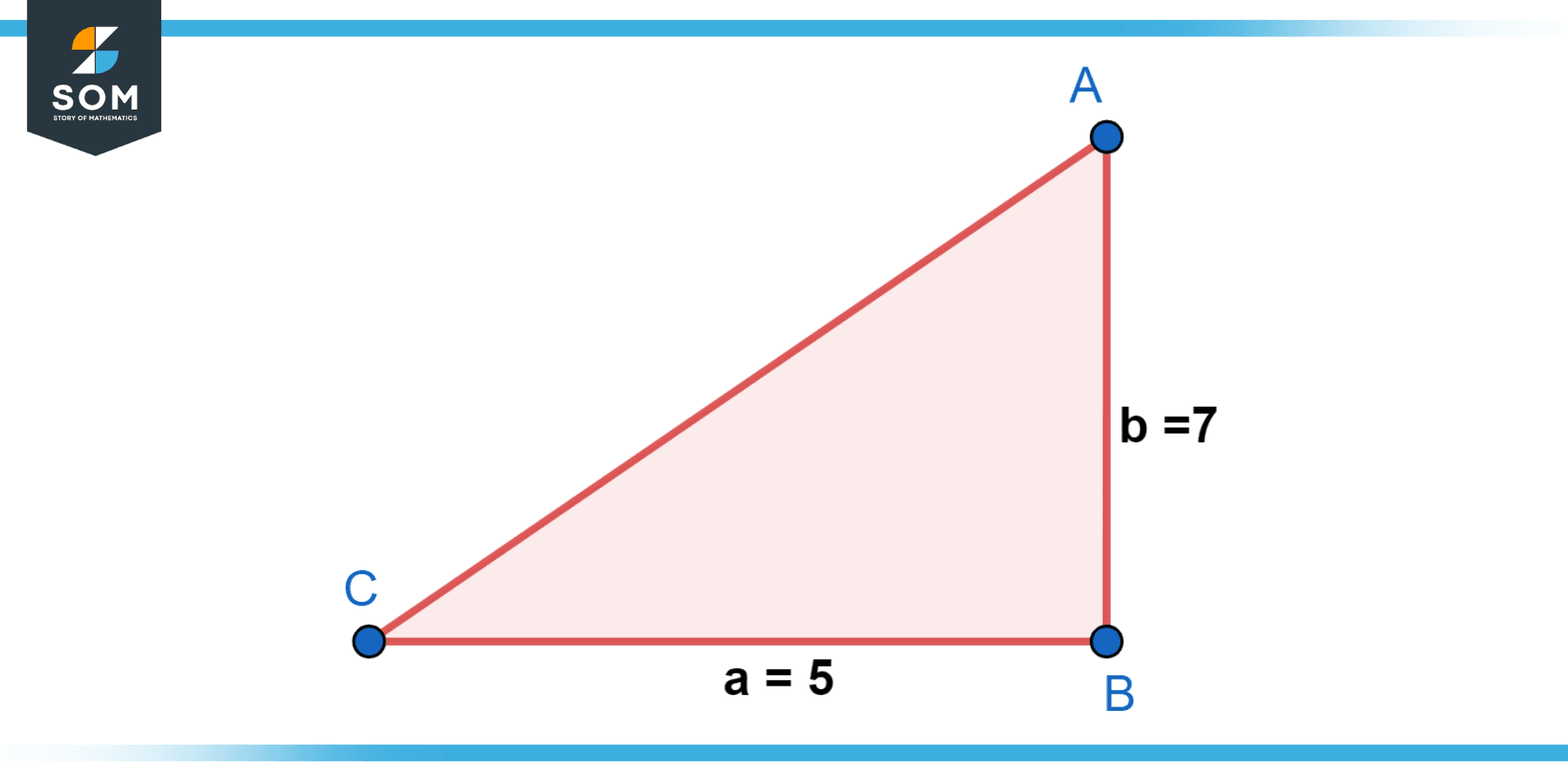
Figure-5.
Solution
Given: Base b = 5 units Height h = 7 units
To find the area A of a right triangle, we can use the formula: A = 0.5 × b × h.
Substituting the given values:
A = 0.5 × 5 × 7
A = 0.5 × 35
A = 17.5 square units
Therefore, the area of the right triangle is 17.5 square units.
Example 4
Determine the length of a leg in a right triangle with a hypotenuse of 13 units and the other leg measuring 5 units.
Solution
Given: Length of hypotenuse c = 13 units Length of one leg a = 5 units
To find the length of the other leg, b, we can use the Pythagorean theorem: c² = a² + b².
Substituting the given values:
13² = 5² + b²
169 = 25 + b²
b² = 169 – 25
b² = 144
When we square the two sides, we discover:
b = √144
b = 12 units
Therefore, the length of the other leg in the right triangle is 12 units.
Example 5
Find the measure of an acute angle in a right triangle if the lengths of the legs are 3 units and 4 units.
Solution
Given: Length of leg a = 3 units Length of leg b = 4 units
To find the measure of an acute angle, we can use trigonometric functions. Let’s calculate the sine of the angle.
Using the formula: sin(A) = opposite / hypotenuse: sin(A) = 3 / 5
Taking the inverse sine (sin⁻¹) of both sides, we find:
A = sin⁻¹(3 / 5)
A ≈ 36.87 degrees
Therefore, the measure of the acute angle in the right triangle is approximately 36.87 degrees.
Example 6
Calculate the perimeter of a right triangle with legs measuring 6 units and 8 units.
Solution
Given: Length of leg a = 6 units Length of leg b = 8 units
To find the perimeter P of a right triangle, we can add the lengths of all sides: P = a + b + c.
Since the perimeter is not given directly, the hypotenuse’s length must be determined, using the Pythagorean theorem: c² = a² + b².
Substituting the given values:
c² = 6² + 8²
c² = 36 + 64
c² = 100
When we square the two sides, we discover:
c = √100
c = 10 units
Now we can calculate the perimeter:
P = 6 + 8 + 10
P = 24 units
Therefore, the perimeter of the right triangle is 24 units.
Example 7
Determine the length of the hypotenuse in a right triangle, with one leg measuring 9 units and the other leg measuring 12 units.
Solution
Given: Length of leg a = 9 units Length of leg b = 12 units
We can apply the Pythagorean theorem to determine the length of the hypotenuse c:: c² = a² + b².
Substituting the given values:
c² = 9² + 12²
c² = 81 + 144
c² = 225
When we square the two sides, we discover:
c = √225
c = 15 units
Therefore, the length of the hypotenuse in the right triangle is 15 units.
Example 8
Find the area of a right triangle with a base of 12 units and a height of 5 units.
Solution
Given: Base b = 12 units Height h = 5 units
To find the area A of a right triangle, we can use the formula: A = 0.5 × b × h.
Substituting the given values:
A = 0.5 × 12 × 5
A = 0.5 × 60
A = 30 square units
Therefore, the area of the right triangle is 30 square units.
All images were created with GeoGebra.
