Antiderivative vs Integral – Definition and Examples

Calculus, the mathematical study of change and motion, often brings two closely related but distinct concepts to the fore: antiderivatives and integrals. While these terms are occasionally used interchangeably in casual conversations, they address different aspects of calculus.

Let’s embark on a journey to understand the nuances between them and explore their significance in the realm of mathematics.

What is the Difference Between an Antiderivative and an Integral 

The main difference between antiderivative and integral is that the antiderivative of a function is essentially a reverse operation to differentiation; it seeks a function whose derivative is the given function.

On the other hand, the integral of a function primarily concerns itself with the area under a function’s curve. While the indefinite integral can be synonymous with the antiderivative, presenting a family of functions as its outcome, the definite integral provides a distinct value, representing the signed area between the function and the x-axis over a specific interval.

In essence, while both concepts operate within the realm of calculus, they serve different mathematical purposes and insights.

What is an Antiderivative?

Definition

The antiderivative of a function $f(x)$ is another function $F(x)$ such that the derivative of $F(x)$ is $f(x)$. In other words, if F′(x) = f(x), then $F(x)$ is an antiderivative of $f(x)$.

Notation

While there’s no standard notation specifically for antiderivatives, they’re sometimes represented as $\int f(x)dx$, without limits of integration.

Uniqueness 

One key aspect to note about antiderivatives is that they aren’t unique. If $F(x)$ is an antiderivative of $f(x)$, then $F(x)+C$, where $C$ is any constant, is also an antiderivative of $f(x)$.

For instance, consider the function $f(x)=2x$. Its antiderivative could be $x^2$, but it could also be $x^2$ $+5$, $x^2$ $-7$, or $x^2$ $+C$, where $C$ is any real number.

What is an Integral?

The integral of a function represents the area under the curve of that function over a certain interval. There are two primary types of integrals in calculus: definite and indefinite.

Indefinite Integral

Definition

The indefinite integral is essentially the antiderivative of a function. It represents the family of functions whose derivative is the given function.

Notation

It’s denoted as $\int f(x)dx$. Note that it doesn’t have upper and lower limits.

Example

The indefinite integral of $f(x)=x$ is ∫x dx = $x^2$ / 2 ​+ C, where $C$ is the constant of integration.

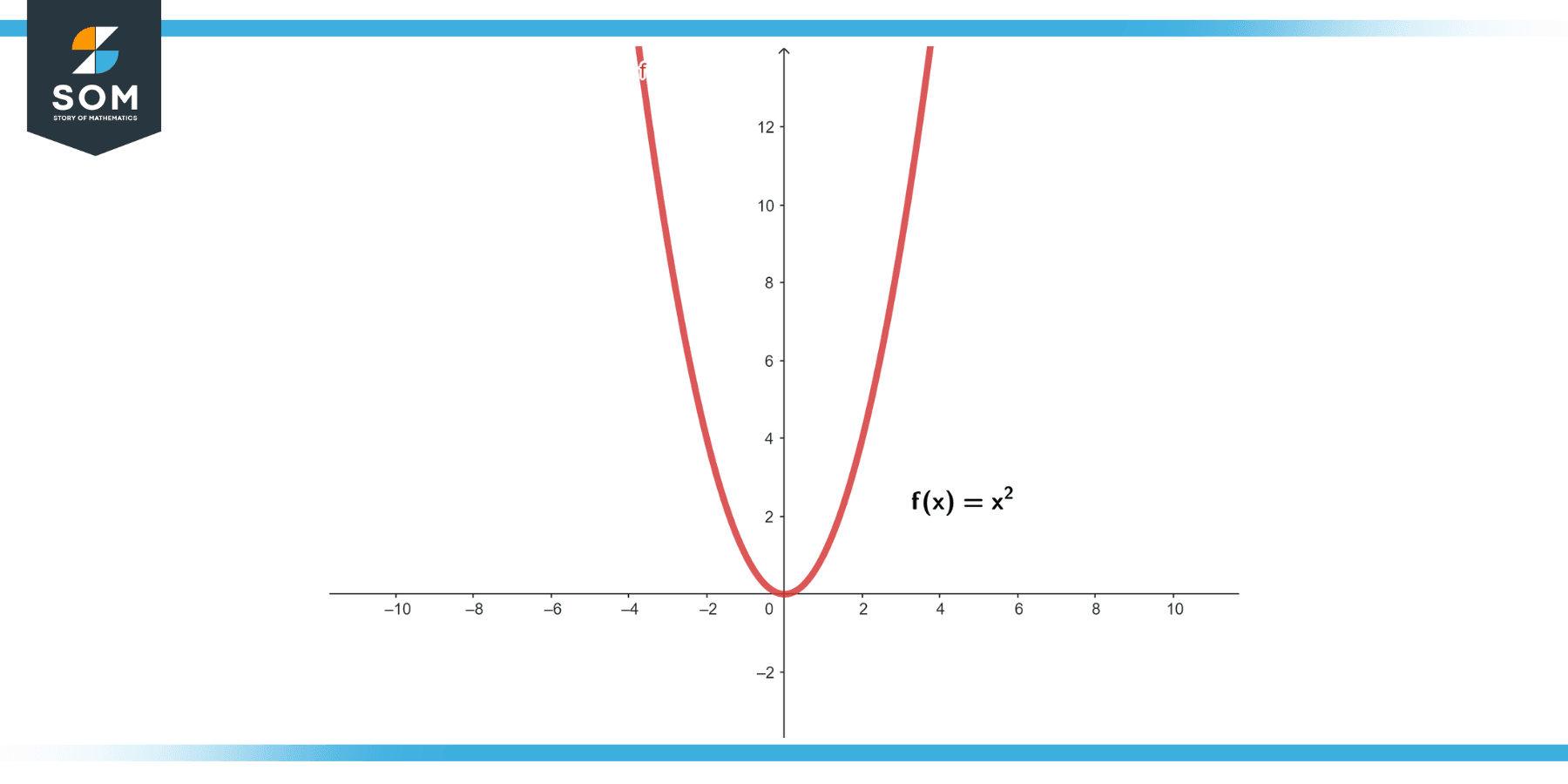
Figure-1.

Definite Integral

Definition

The definite integral computes the signed area between the function and the x-axis over a specified interval [a, b].

Notation

It’s denoted with upper and lower limits: ∫​f(x) dx, from a to b.

Example

For $f(x)=x$ over the interval [0,2], the definite integral is $\int xdx$. for [0,2] This calculates the area under the curve from 0 to 2, which results in a value of 2.

Distinguishing Between the Antiderivative and Integral

• Purpose

  • Antiderivative: Finds a function whose derivative is the given function.
  • Integral: Computes areas under curves (definite) or represents the family of functions whose derivative is the given function (indefinite).

• Uniqueness

  • Antiderivative: Not unique due to the integration constant.
  • Definite Integral: Produces a unique real number since it computes a specific area.
  • Indefinite Integral: Not unique for the same reasons as the antiderivative.

• Physical Significance

  • Antiderivative: Often used in physics to find quantities when rates of change are known, such as determining position from velocity.
  • Integral: Used to calculate quantities like area, volume, work, etc.

Exercise 

Example 1

Function: $f(x)=\; \$x^2\$$

Solution

Antiderivative:

∫f(x) dx = ∫$x^2$ dx = $x^3$ / 3​ + C

where $C$ is an integration constant.

Definite Integral (over the interval [0,2]):

∫$x^2$ dx = [$x^3$ / 3​], form 0 to 2​

∫$x^2$ dx =8 / 3 ​− 0 = 8 / 3​

Example 2

Function: f(x) = ∫$e^x$ dx

Figure-2.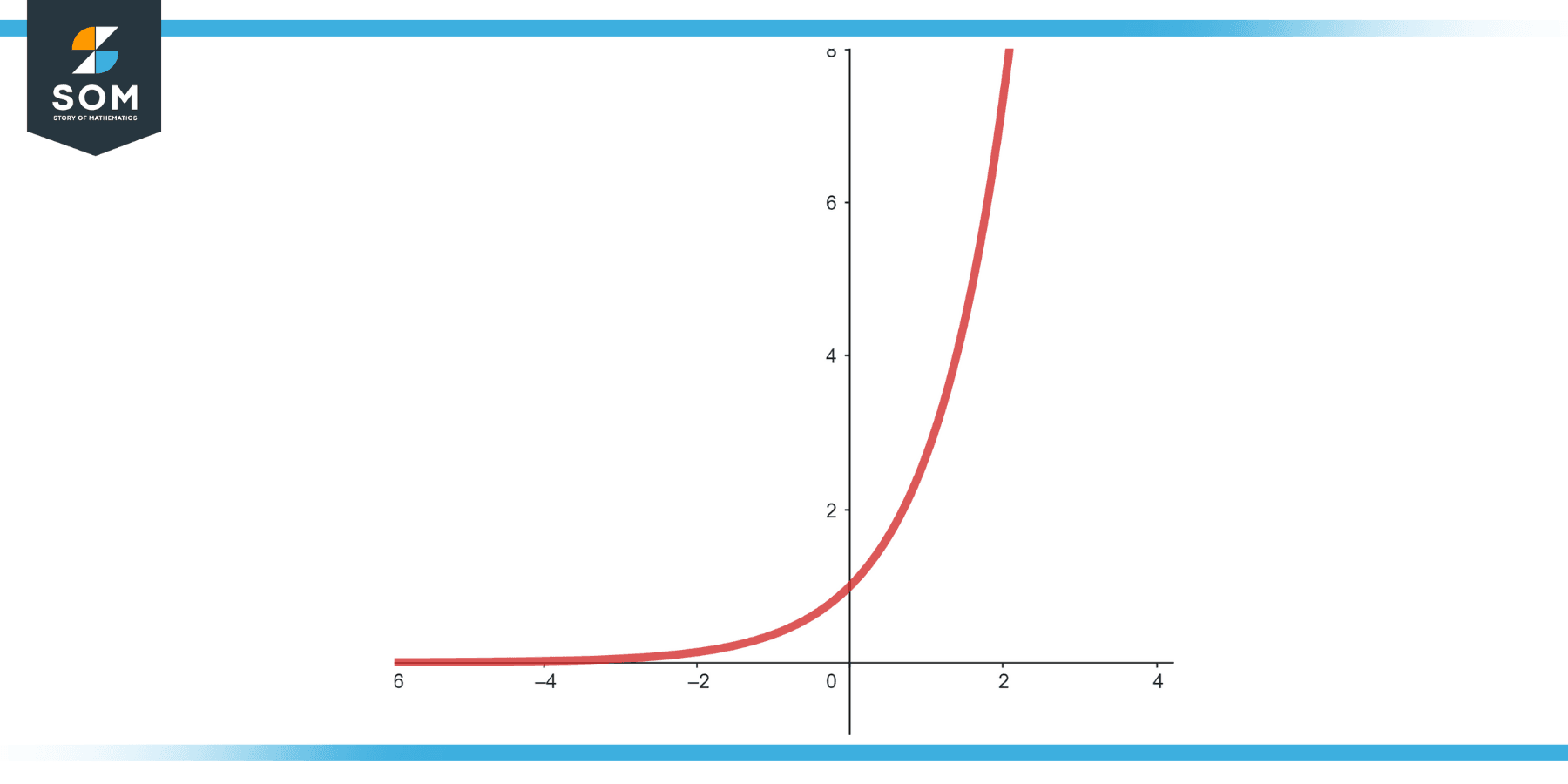

Solution

Antiderivative:

∫f(x) dx =∫$e^x$ dx = $e^x$ + C

Definite Integral (over the interval [0,1]):

∫f(x) dx = ∫$e^x$ dx, from 0 to 1

∫f(x) dx =  [$e^x$], for x=0 to x=1

∫f(x) dx ​= $e^{-1}$

Example 3:

Function: $f(x)=\sin (x)$

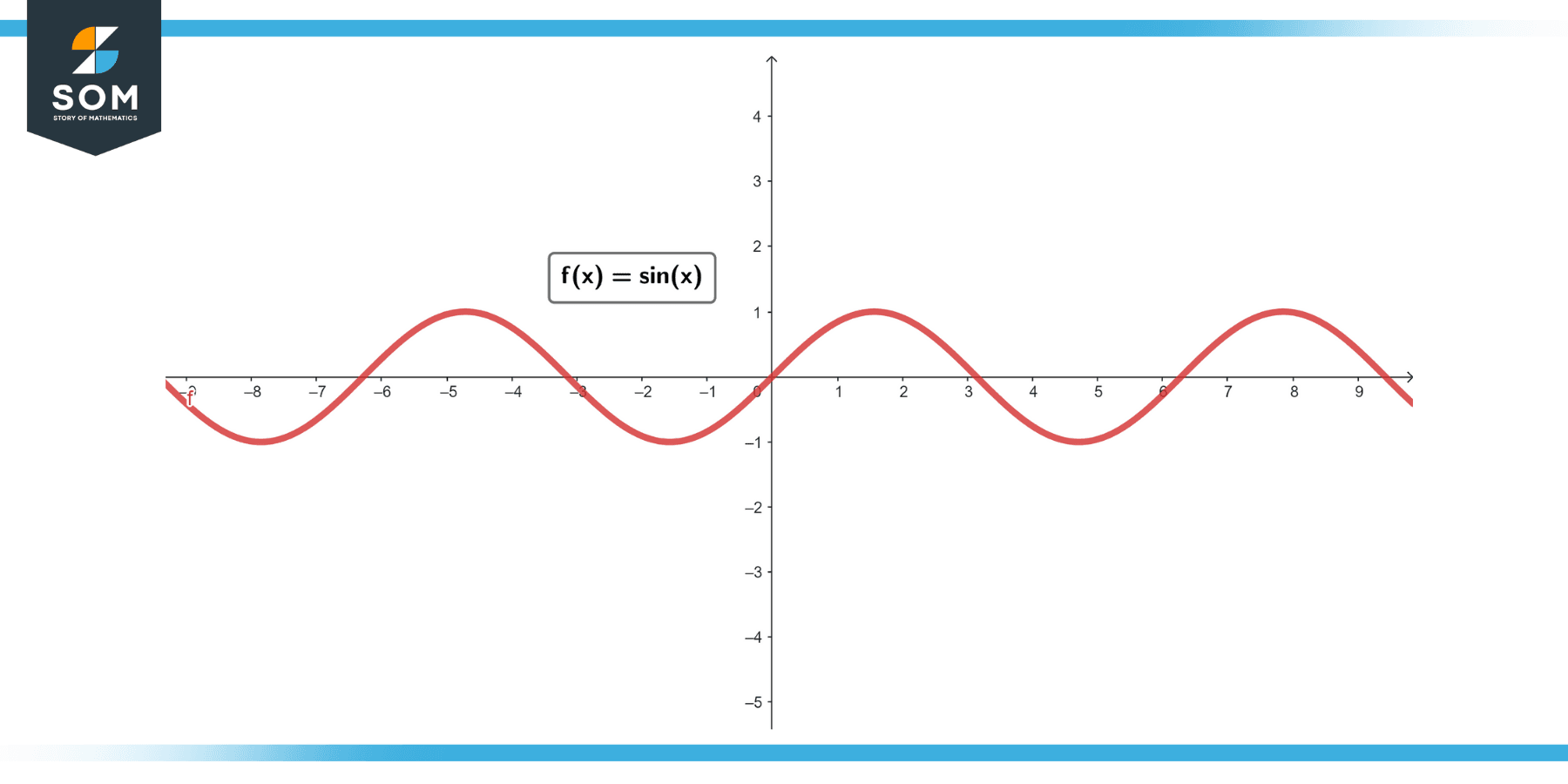
Figure-3.

Solution

Antiderivative:

$\int f(x)dx=\int \sin (x)dx=-\cos (x)+C$

Definite Integral (over the interval [0,π]):

∫​sin(x) dx = [−cos(x)], for x=0 to x=π

∫​sin(x) dx = 2

Real-World Implications:

The profound concepts of antiderivatives and integrals aren’t confined within the boundaries of academic mathematics; they have extensive applications in real-world scenarios. Understanding their real-world implications provides a richer appreciation for these mathematical tools.

• Physics

  • Antiderivative: In kinematics, if the velocity of an object (rate of change of position) is known, antiderivatives are used to determine its position or the path it has traveled over time.
  • Integral: When calculating work done by a variable force over a specific distance or the electric charge stored over a changing voltage, definite integrals come into play.

• Engineering

  • Antiderivative: Engineers often resort to antiderivatives when they need to reverse engineer rates of change, like determining displacement from a known stress-strain curve.
  • Integral: In civil engineering, integrals are used to compute the area and volume essential for design, especially in complex structures like bridges and dams. Similarly, in electrical engineering, integrals help in analyzing changing currents and voltages over time.

• Economics

  • Antiderivative: If an economist knows the marginal cost (the cost to produce one additional item), they can use the antiderivative to find the total cost function.
  • Integral: Economists use definite integrals to calculate quantities like consumer and producer surpluses, which provide insights into market efficiency and welfare.

• Biology and Medicine

  • Antiderivative: Used in pharmacokinetics, the study of how drugs are absorbed, distributed, metabolized, and excreted in the body. Knowing the rate at which a drug leaves the bloodstream can help determine the drug’s concentration at different times.
  • Integral: In modeling biological processes, integrals assist in computations like determining the total number of cells in a growing tumor over time or understanding how blood volume changes in response to certain conditions.

• Environmental Science

  • Antiderivative: Useful in predicting how pollutants disperse in natural waters over time, based on their rate of spread.
  • Integral: When estimating the total amount of materials required to restore a habitat or the total energy received by a surface during the day, integrals provide the necessary computational tools.

Astronomy

• • Antiderivative: Helps in determining the orbits of celestial bodies based on their speed and direction.
  • Integral: Used to compute the total luminosity of stars or the total mass of galaxies within certain radii.

All images were created with GeoGebra.