 The triangle proportionality theorem states that if we draw a line parallel to one side of a triangle so that it intersects the remaining two sides, then both sides are divided in the same proportion or divided equally.
The triangle proportionality theorem states that if we draw a line parallel to one side of a triangle so that it intersects the remaining two sides, then both sides are divided in the same proportion or divided equally.
The triangle proportionality theorem is also known as the side-splitting theorem as it splits both sides into equal parts or equal proportions.
This topic will help you learn and understand the concept of the triangle proportionality theorem, along with its proof and related numerical examples.
What Is Triangle Proportionality Theorem?
The triangle proportionality theorem is a theorem that states that if we draw a line parallel to one side of a triangle so that it intersects the remaining two sides, then both sides are divided equally. If a line is drawn parallel to one side of a triangle, it is called the mid-segment of the triangle.
The mid-segment of a triangle divides the two sides of the triangle in equal proportions according to the triangle proportionality theorem.
In geometry, two figures can be similar, even if they have different lengths or dimensions. For example, no matter how much the radius of a circle differs from another circle, the shape looks the same. The same is the case with a square — no matter what is the perimeter of a square is, the shapes of different squares look similar even if the dimensions vary.
When we are discussing the similarities of two or more triangles, then certain conditions must be met for the triangles to be declared similar:
1. The corresponding angles of the triangles must be equal.
2. The corresponding sides of the compared triangles must be in proportion to each other.
For example, if we are comparing $\triangle ABC$ with $\triangle XYZ$, then both of these triangles will be called similar if:
1. $\angle A$ = $\angle X$ , $\angle B$ = $\angle Y$ and $\angle C$ = $\angle Z$
2. $\dfrac{AB}{XY}$ = $\dfrac{BC}{YZ}$ = $\dfrac{CA}{ZX}$
Consider this $\triangle XYZ$. If we draw a parallel line $CD$ to the $YZ$ side of the triangle, then by the definition of triangle proportionality theorem, the ratio of $XC$ to $CY$ would be equal to the ratio of $XD$ to $DZ$.
$\dfrac{XC}{CY} = \dfrac{XD}{DZ}$
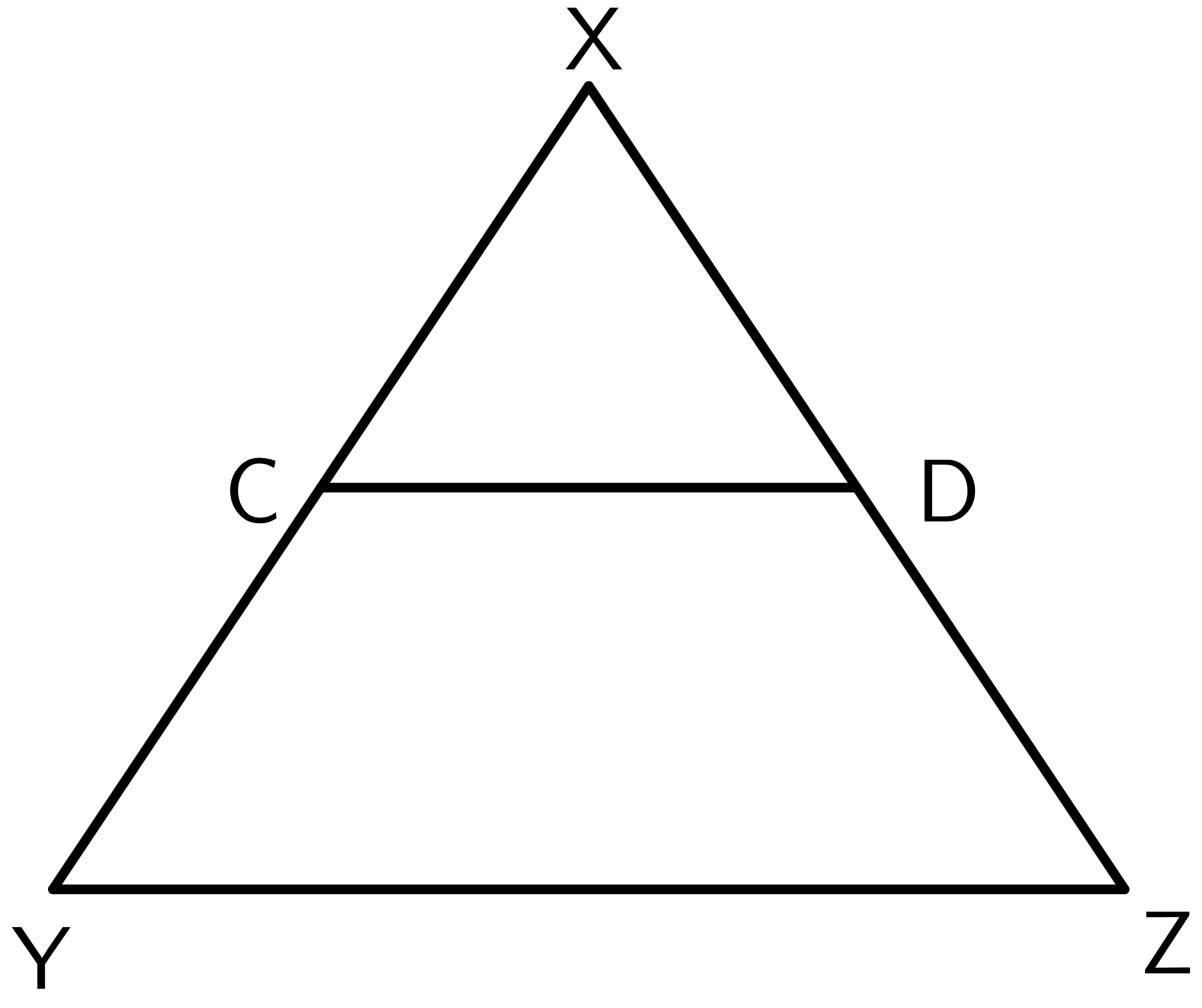
How To Use Triangle Proportionality Theorem
The following steps should be kept in mind while solving problems using the triangle proportionality theorem:
- Identify the parallel line intersecting the two sides of the triangle.
- Identify similar triangles. We can identify similar triangles by comparing the sides proportion of the triangles or by using the AA similarity theorem. AA or Angle, Angle similarity theorem states that if two angles of a triangle are congruent to two angles of the other triangles, then both triangles are similar.
- Identify the corresponding sides of the triangles.
Proof of Triangle Proportionality Theorem
If a line is drawn parallel to one side of a triangle to intersect the other two sides, then according to the triangle proportionality theorem, both sides are divided in equal proportions. We have to prove that $\dfrac{XC}{CY}$ = $\dfrac{XD}{DZ}$ for the triangle given below.
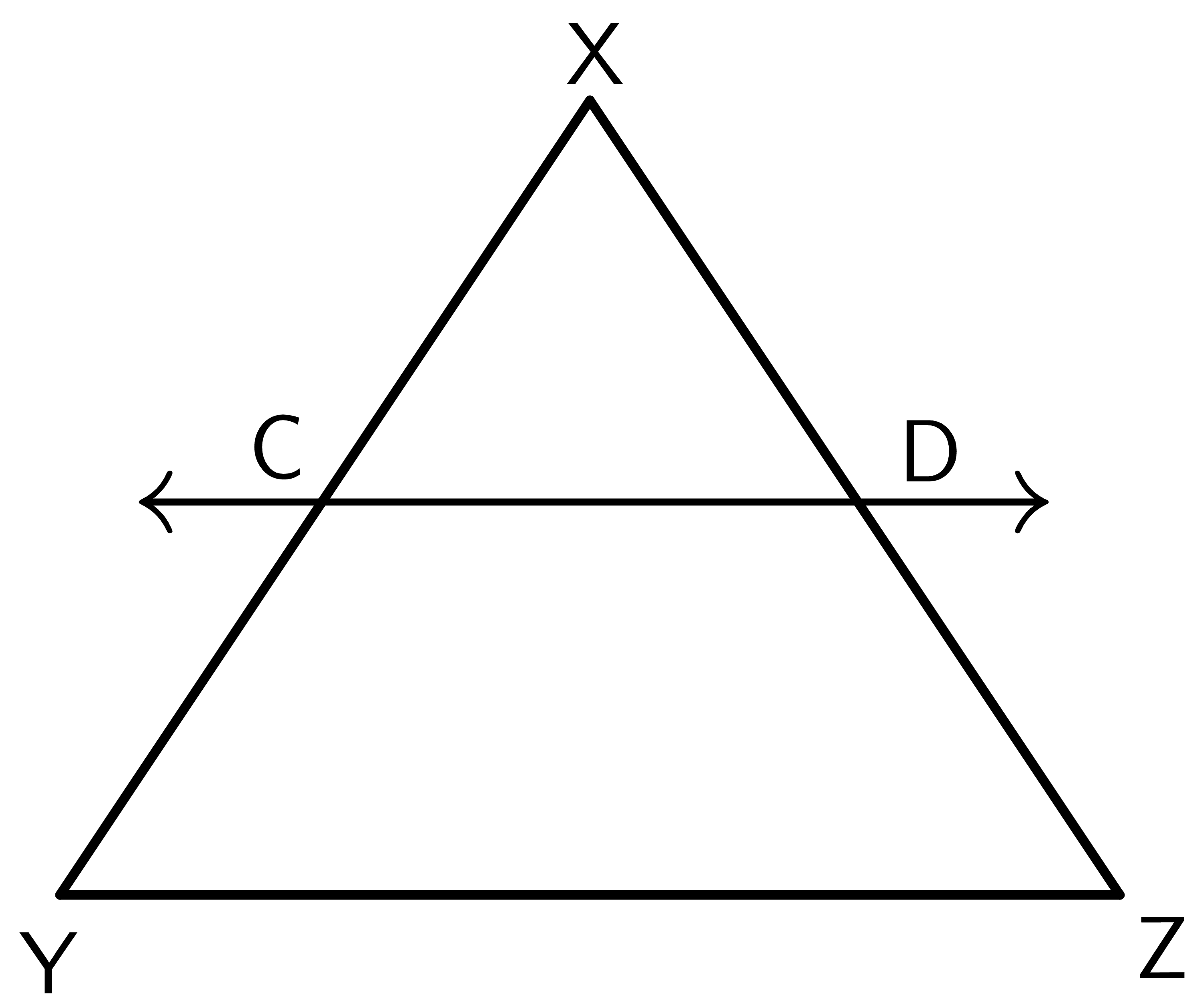
Sr. No | Statement | Reasons |
| 1. | $\angle XCD\cong \angle XYZ$ | The parallel lines form congruent angles |
| 2. | $\triangle XYZ \cong \triangle XCD$ | AA similarity states that if two angles of both triangles are the same, they are congruent. |
| 3. | $\dfrac{XC}{CY} = \dfrac{XD}{DZ}$ | $\triangle XYZ \cong \triangle XCD$, hence the corresponding sides of both triangles are similar. |
| 4. | $\dfrac{CY}{XC} = \dfrac{DZ}{XD}$ | Applying the reciprocal property |
Proof of Converse Triangle Proportionality Theorem
The converse triangle proportionality theorem states that if a line intersects the two sides of a triangle so that it divides them in equal proportions, then that line is parallel to the third or last side of the triangle.
Take the same figure which was used in the proof of triangle proportionality theorem. We are given that $\dfrac{XC}{CY} = \dfrac{XD}{DZ}$ and we have to prove $CD || YZ$.
$\dfrac{XC}{CY} = \dfrac{XD}{DZ}$
Taking the reciprocal and we get:
$\dfrac{CY}{XC} = \dfrac{DZ}{XD}$
Now add “$1$” to the both sides.
$\dfrac{CY}{XC} +1 = \dfrac{DZ}{XD} +1$
$\dfrac{CY+XC}{XC} = \dfrac{DZ+XD}{XD}$
We know that $XY = XC + CY$ and $XZ = DZ + XD$.
$\dfrac{XY}{XC} =\dfrac{XZ}{XD}$
As $\angle X$ is included in both $\triangle XYZ$ and $\triangle XCD$, we can use the SAS congruence for similar triangles to say that $\triangle XYZ \cong \triangle XCD$. If both the triangles are similar, then angle $\angle XCD \cong <XYZ$. The condition $\angle XCD \cong <XYZ$ is true when $CD || YZ$.
Hence it is proven that when the line cuts the two sides of triangles in equal proportion, it is parallel to the third side.
Let us write the proof in tabular form.
Sr. No | Statement | Reasons |
| 1. | $\dfrac{XC}{CY} = \dfrac{XD}{DZ}$ | Given |
| 2. | $\dfrac{CY}{XC} = \dfrac{DZ}{XD}$ | Applying the reciprocal property |
| 3. | $\dfrac{CY}{XC}+1 = \dfrac{DZ}{XD}+1$ | Adding 1 on the both sides |
| 4. | $\dfrac{CY+XC}{XC} = \dfrac{DZ+XD}{XD}$ | Adding the fractions |
| 5. | $\dfrac{XY}{XC} =\dfrac{XZ}{XD}$ | Line segment addition |
| 6. | $\angle X \cong <X$ | Reflexive property |
| 7. | $\triangle XYZ \cong \triangle XCD$ | SAS property for similar triangles |
| 8. | $\angle XCD \cong \angle XYZ$ | AA property for similar triangles |
| 9. | $CD||YZ$ | Converse angles gives us parallel sides |
Applications of Triangle Proportionality Theorem
- The triangle proportionality theorem is used in construction purposes. For example, if you want to build a house with triangular support beams for the roof, then utilizing the triangle proportionality theorem will help you a lot.
- It helps build roads and caves in triangular mountains.
- It is used in making tables of different sizes and lengths.
Example 1:
In a triangle $XYZ$, $CD|| YZ$ while $XC = 3 cm$, $CY = 1cm$ and $XD = 9 cm$. Find the length of $DZ$.
Solution:
The formula for triangle proportional theorem is given as:
$\dfrac{XC}{CY} = \dfrac{XD}{DZ}$
$\dfrac{3}{1} = \dfrac{9}{DZ}$
$DZ = \dfrac{9}{3}$
$DZ = 3 cm$
Example 2:
In a triangle $XYZ$, $CD|| YZ$ while $XC = 6 cm$, $CY = 1.5 cm$ and $DZ = 3 cm$. Find the length of $XD$.
Solution:
The formula for triangle proportional theorem is given as:
$\dfrac{XC}{CY} = \dfrac{XD}{DZ}$
$\dfrac{6}{1.5} = \dfrac{XD}{3}$
$4 = \dfrac{XD}{3}$
$XD = 4 \times 3$
$DZ = 12 cm$
Example 3:
Use the triangle proportionality theorem to find the value of ” $x$” for the figure below.
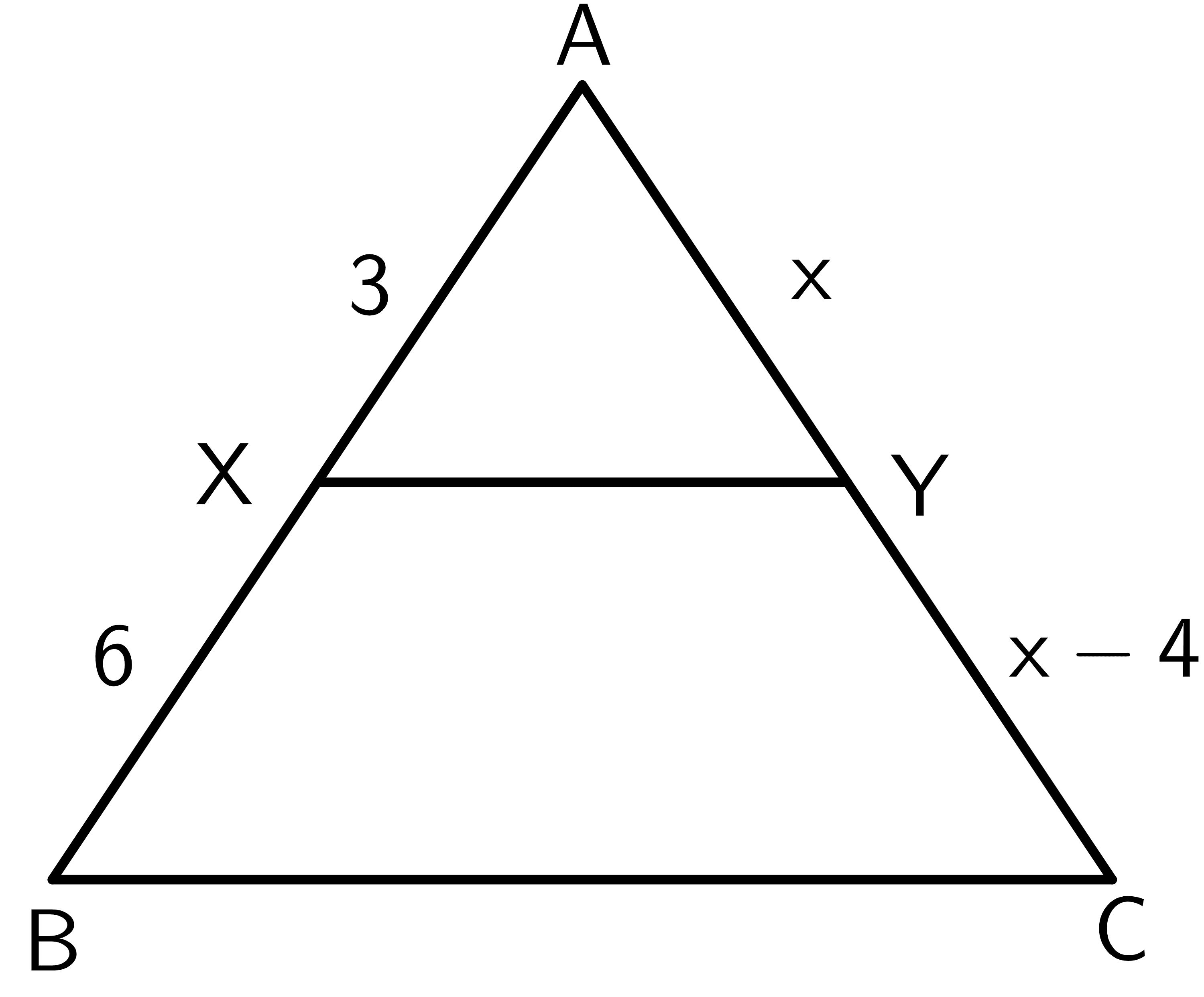
Solution:
The formula for triangle proportional theorem is given as:
$\dfrac{AX}{XB} = \dfrac{AY}{YC}$
$\dfrac{3}{6} = \dfrac{4}{x-4}$
$ 3 (x- 4) = 6\times 4$
$ 3x – 12 = 24$
$ 3x = 24 + 12$
$ 3x = 36$
$ x = \dfrac{36}{3} = 12$
Example 4:
Use the triangle proportionality theorem to find the value of ” $x$” for the figure below.
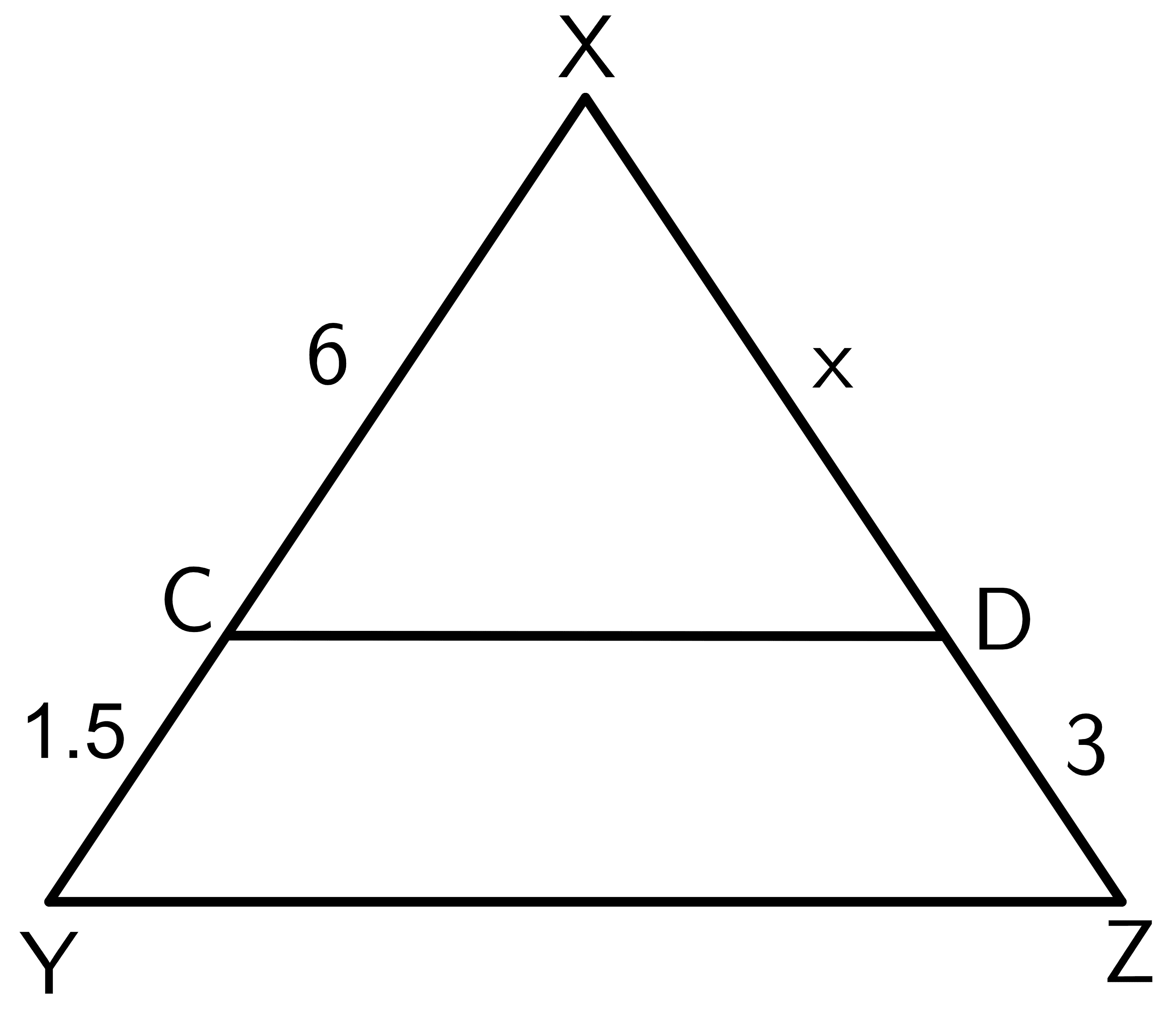
Solution:
The formula for triangle proportional theorem is given as:
$\dfrac{XC}{CY} = \dfrac{XD}{DZ}$
$\dfrac{6}{1.5} = \dfrac{x}{3}$
$4 = \dfrac{x}{3}$
$x = 4 \times 3$
$x = 12 cm$
Example 5:
A team of civil engineers is designing a model for a highway, and they want to build a tunnel inside a mountain. Suppose the mountain stopping the path is like a right-angle triangle, as shown in the figure below. The total height of the mountain is known to be $500$ ft.
The distance of the tunnel’s starting point to the top is $100$ feet. The total length of another side of the mountain is “$x$”, while we know the length from the tunnel exit point to the bottom of the mountain, which is $500$ ft. You are required to help the engineers calculate the length of the tunnel.
Solution:
If we solve the right triangle using proportionality theorem then it is called as right triangle proportionality theorem.
We know that $AB = AP + PB$.
$AB$ is the total length of one side of the mountain and it is equal to $500ft$, while $AP$ is the length from the top of mountain to the starting location of the tunnel.
With this information, we can write:
$AB = AP + PB$
$500 = 100 + PB$
$PB = 500 – 100$
$PB = 400 ft$.
We have the value of $PB$ and now we will calculate the value of “$x$”.
The formula for triangle proportional theorem is given as:
$\dfrac{AP}{PB} = \dfrac{AQ}{QC}$
$\dfrac{100}{400} = \dfrac{x-500}{500}$
$\dfrac{1}{4} = \dfrac{x-500}{500}$
$ 1\times 500 = (x-500) 4$
$ 500 = 4x – 2000$
$ 4x = 2000 + 500$
$ 4x = 2500$
$ x = \dfrac{2500}{4} = 625 $
So the value from the top to the bottom of the mountain of the side $AC$ is $625 ft$. If we subtract $QC$ from $AC$, we will get the length of $AQ$.
$ AQ = AC – QC = 625 – 500 = 125 ft$.
We were asked to find the length of the tunnel and that would be the length of $PQ$. The length of $PQ$ can now easily be calculated using Pythagorean theorem.
$AQ^{2}= PQ^{2}+ AP^{2}$
$125^{2}= PQ^{2}+ 100^{2}$
$ PQ = \sqrt{125^{2}+100^{2}}$
$ PQ = \sqrt{25,625}$
$ PQ = 160 ft$ approx.
Practice Questions:
- In a triangle $XYZ$, $CD|| YZ$ while $CY = 6 cm$, $XD = 9 cm$ DZ = 15cm. Find the length of $XC$.
- Use the triangle proportionality theorem to find the value of ” $x$” for the figure given below.
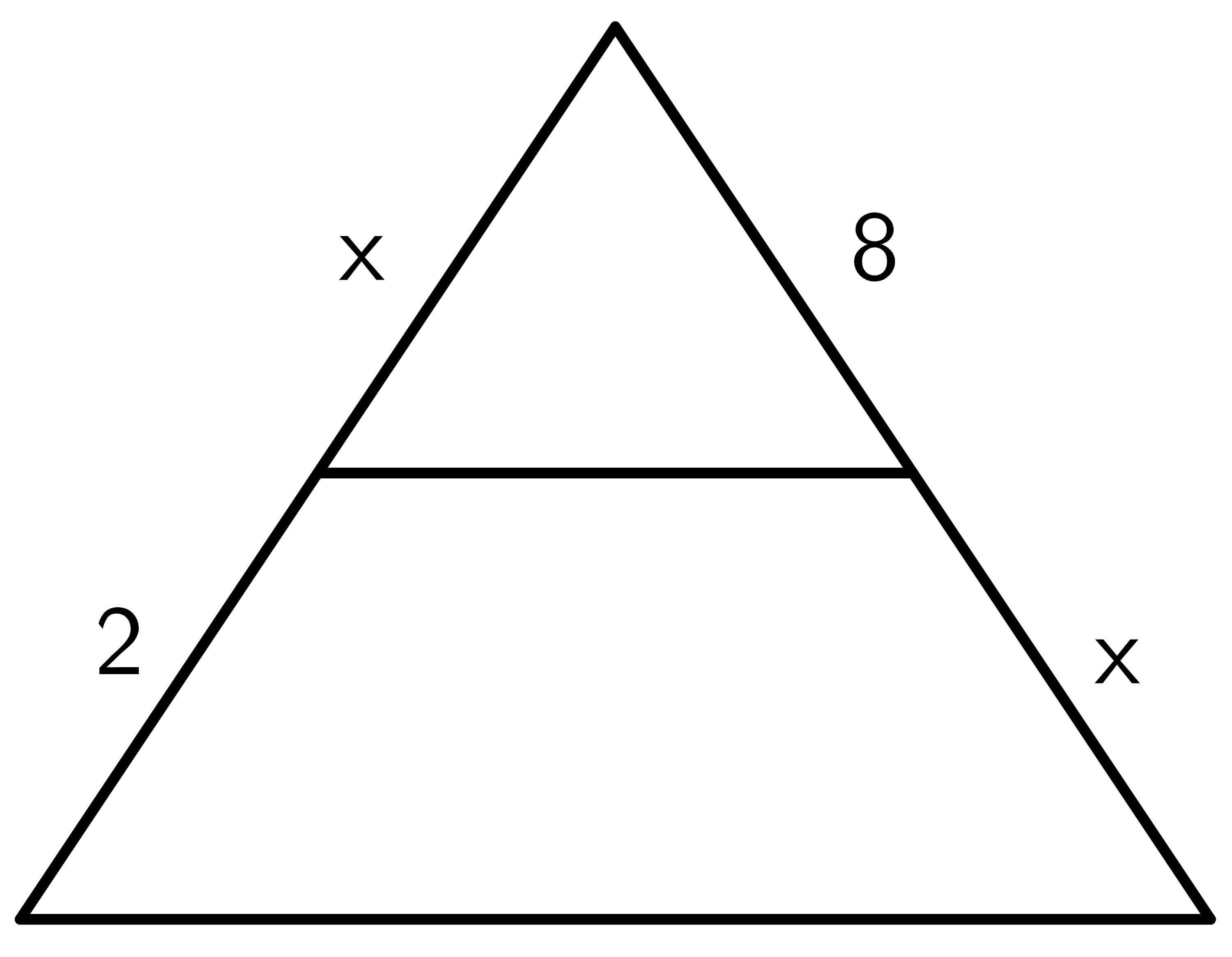
3. Use the triangle proportionality theorem to find the value of ” $x$” for the figure given below.
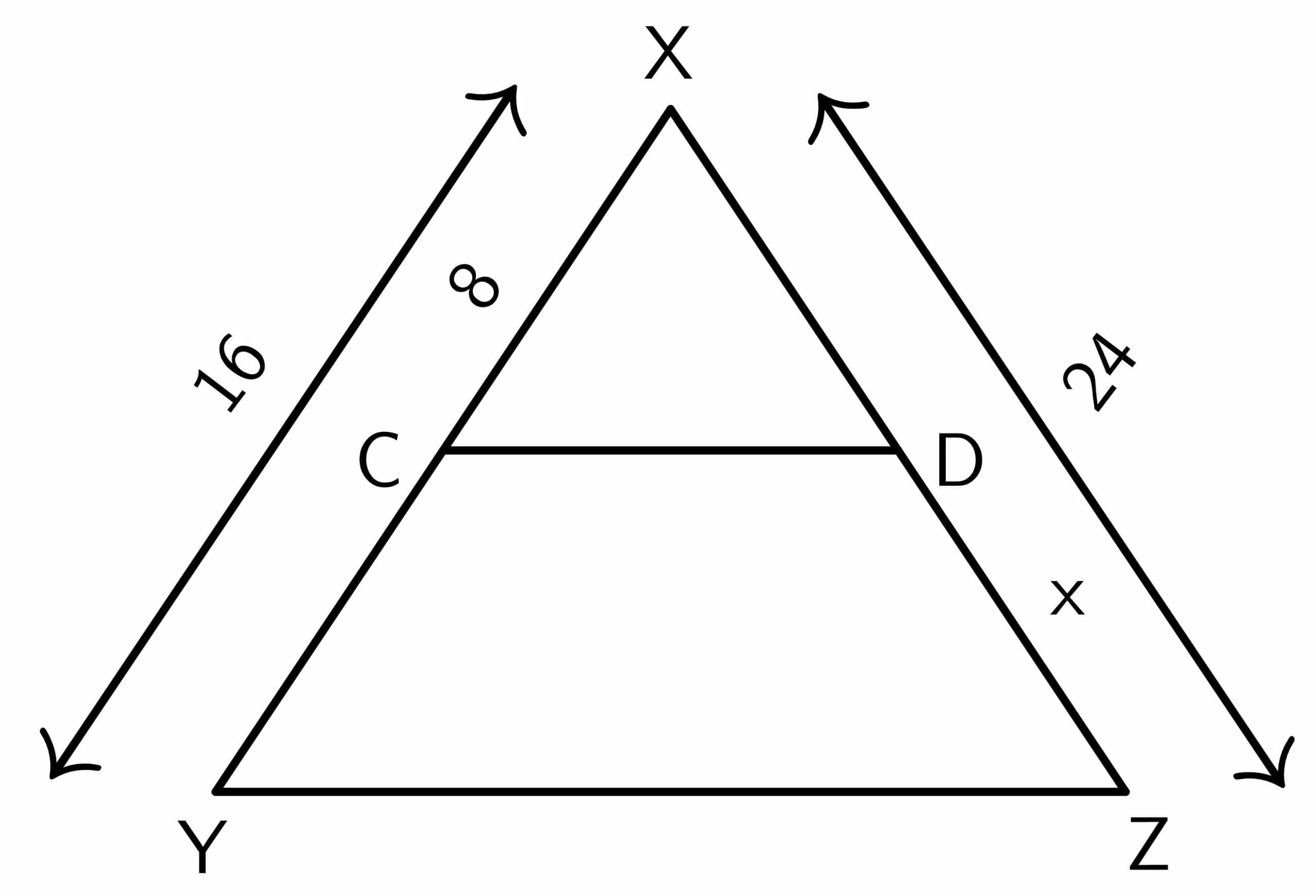
Answer Key:
1.
$\dfrac{XC}{CY} = \dfrac{XD}{DZ}$
$\dfrac{XC}{6} = \dfrac{9}{15}$
$XC = (\dfrac{9}{15})\times 6$
$XC = \dfrac{18}{5}$
$XC = 3.6 cm$.
2.
$\dfrac{x}{2} = \dfrac{8}{x}$
$x^{2} = 8\times 2$
$x^{2} = 16$
$ x = 4 cm$.
3.
$\dfrac{CY}{XY} = \dfrac{DZ}{XZ}$
$\dfrac{XY-XC}{XY} = \dfrac{DZ}{XZ}$
$\dfrac{16 – 8 }{16} = \dfrac{x}{24}$
$\dfrac{8 }{16} = \dfrac{x}{24}$
$\dfrac{1 }{2} = \dfrac{x}{24}$
$ x = \dfrac{24}{2} = 12$
