\(\dfrac{1}{4\pi\epsilon_0}\).
- What is the electric potential $V_{tot}$ at the center of the square? Make the usual assumption that the potential tends to zero far away from a charge. Express your answer in terms of $q,d,$ and appropriate constants.
- What is the contribution $U_{2q}$ to the electric potential energy of the system, due to interactions involving the charge $2q$? Express your answer in terms of $q, d$, and appropriate constants.
- What is the total electric potential energy $U_{tot}$ of this system of charges? Express your answer in terms of $q, d,$ and appropriate constants.
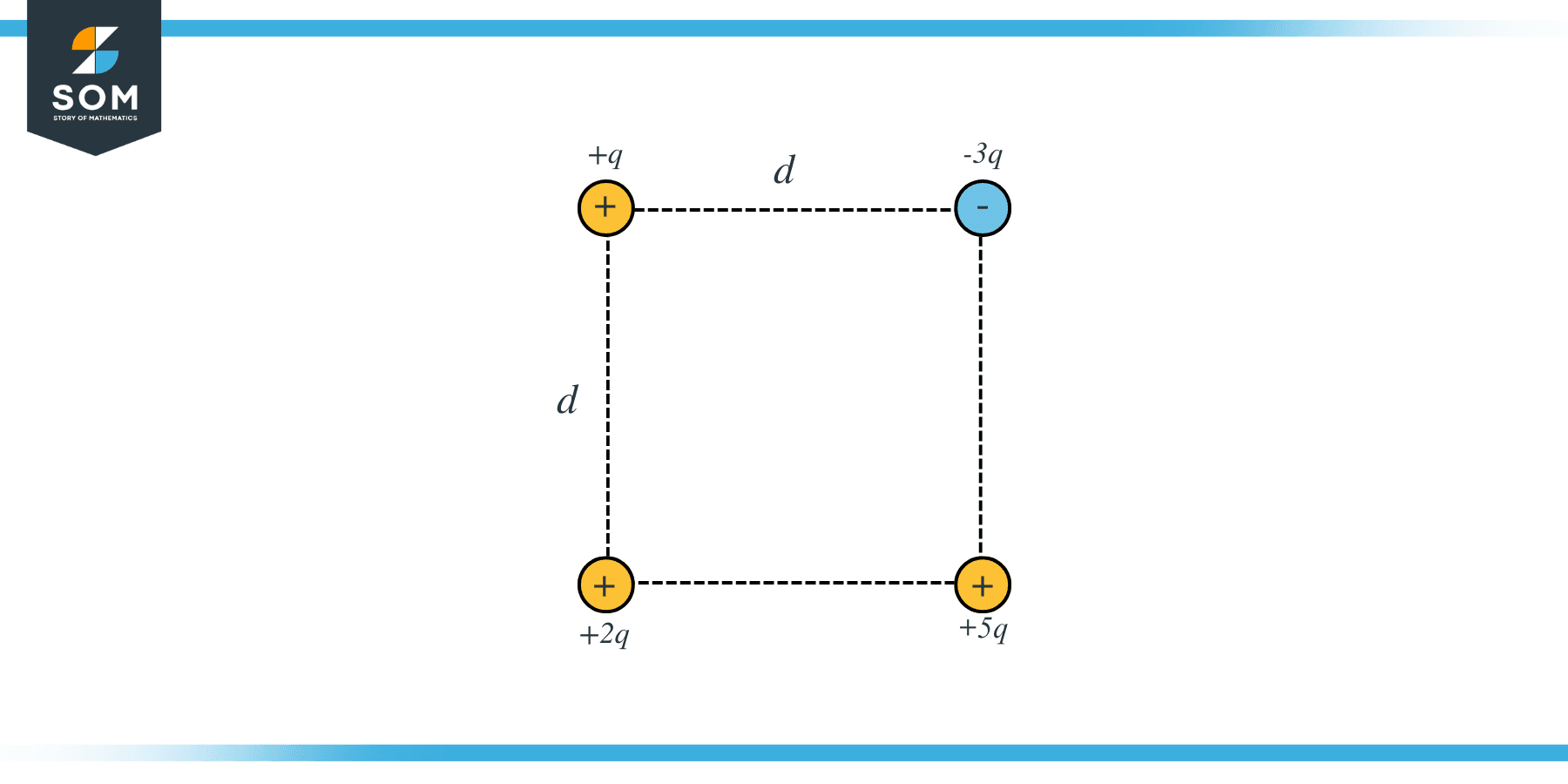
This question aims to find the electric potential energy following the given diagram.
A type of energy retained by an object as a result of its position in relation to other objects, internal stresses, electric charge, or other factors is said to be potential energy.
The object’s gravitational potential energy, which relies on its mass and distance from the center of mass of some other object, the electric potential energy of an electric charge in an electric field, and the elastic potential energy of an extended spring, are all examples of potential energy.
The amount of work required to move a unit charge from a point of reference to a specified location in resistance to an electric field is referred to as electric potential. The electric potential magnitude is determined by the amount of work done in moving the object from one point to another in resistance to an electric field.
The electric potential for any charge is calculated by dividing the potential energy by the quantity of charge. An increase in the potential energy of an object is observed when it moves against an electric field.
In the case of a negative charge, the potential energy decreases when moved with an electric field. Unless the unit charge passes through a varying magnetic field, its potential at any given point is independent of the path taken.
Expert Answer
The electric potential can be expressed as:
$V=\dfrac{kq}{d}$
Where $d$ is the distance
and $q$ is the charge,
and $k=\dfrac{1}{4\pi\epsilon_0}$ is the Coulomb’s constant.
According to the figure, the distance from center of the square to any charge is:
$\dfrac{\sqrt{d^2+d^2}}{2}$
$=\dfrac{\sqrt{2}\,d}{2}$
$=\dfrac{d}{\sqrt{2}}$
And hence, the electric potential at the center of the square is:
$V_{tot}=\dfrac{(k)(2q)}{\dfrac{d}{\sqrt{2}}}+\dfrac{(k)(q)}{\dfrac{d}{\sqrt{2}}}-\dfrac{(k)(3q)}{\dfrac{d}{\sqrt{2}}}+\dfrac{(k)(5q)}{\dfrac{d}{\sqrt{2}}}$
$=\dfrac{\sqrt{2}\,kq}{d}(2+1-3+5)$
$=5\sqrt{2}\dfrac{kq}{d}$
Let $q_1$ be the charge of point charge $1$, $q_2$ be the charge of point charge $2$, then electric potential energy is given by:
$U=\dfrac{q_1q_2k}{d}$
Now, the electric potential energy due to the charges $+2q$ and $+5q$ is:
$U_{25}=\dfrac{(+2q)(+5q)k}{d}$
$=\dfrac{(10q^2)k}{d}$
And the electric potential energy due to the charges $+2q$ and $+q$ is:
$U_{21}=\dfrac{(+2q)(+q)k}{d}$
$=\dfrac{(2q^2)k}{d}$
From the figure, the distance between the charges $+2q$ and $-3q$ is:
$\sqrt{d^2+d^2}$
$=\sqrt{2}\,d$
So the electric potential energy due to the charges $+2q$ and $-3q$ is:
$U_{23}=\dfrac{(+2q)(-3q)k}{\sqrt{2}\,d}$
$=-\dfrac{(6q^2)k}{\sqrt{2}\,d}$
Hence, the system’s total electric potential energy because of the interactions including the charge $+2q$ is:
$U_{2q}=U_{25}+U_{21}+U_{23}$
$=\dfrac{(10q^2)k}{d}+\dfrac{(2q^2)k}{d}-\dfrac{(6q^2)k}{\sqrt{2}\,d}$
$=\dfrac{kq^2}{d}\left[10+2-\dfrac{6}{\sqrt{2}}\right]$
$=\dfrac{(7.76)kq^2}{d}$
Lastly, we find the total electric potential energy for the given system as:
$U_{tot}=U_{25}+U_{21}+U_{23}+U_{51}+U_{53}+U_{31}$
Since $U_{25},U_{21},U_{23}$ are known from above, so continuing the calculation for $U_{51},U_{53},U_{31}$ as:
The distance between the charges $+5q$ and $+q$ is:
$\sqrt{d^2+d^2}$
$=\sqrt{2}\,d$
So, $U_{51}=\dfrac{(+5q)(+q)k}{\sqrt{2}\,d}$
$=\dfrac{(5q^2)k}{\sqrt{2}\,d}$
Also,
$U_{53}=\dfrac{(+5q)(-3q)k}{d}$
$=-\dfrac{(15q^2)k}{d}$
And,
$U_{31}=\dfrac{(-3q)(+q)k}{d}$
$=-\dfrac{(3q^2)k}{d}$
Finally, $U_{tot}=\dfrac{(10q^2)k}{d}+\dfrac{(2q^2)k}{d}-\dfrac{(6q^2)k}{\sqrt{2}\,d}+\dfrac{(5q^2)k}{\sqrt{2}\,d}-\dfrac{(15q^2)k}{d}-\dfrac{(3q^2)k}{d}$
$U_{tot}=\dfrac{kq^2}{d}\left(10+2-\dfrac{6}{\sqrt{2}}+\dfrac{5}{\sqrt{2}}-15-3\right)$
$U_{tot}=\dfrac{kq^2}{d}(-6.71)$
$U_{tot}=-\dfrac{(6.71)kq^2}{d}$
Example
Given two equal charges, if the electric potential energy between them is doubled, what will be the change in the distance between the particles?
Solution
Since $U=\dfrac{q_1q_2k}{d}$
Also, given that:
$U_2=2U$
It is known that an inverse relationship exists between the electric potential energy and the distance between two charges, therefore:
$2U=\dfrac{q_1q_2k}{y(d)}$
$2U=\dfrac{q_1q_2k}{\left(\dfrac{1}{2}\right)d}$
$2U=\dfrac{2q_1q_2k}{d}$
Hence, if the energy doubles, the distance is halved.
