Physics Q&A Archives - The Story of Mathematics - A History of Mathematical Thought from Ancient Times to the Modern Day

Four point charges form a square with sides of length d, as shown in the figure. In the questions that follow, use the constant k in place of

(dfrac{1}{4piepsilon_0}). What is the electric potential $V_{tot}$ at the center of the square? Make the usual assumption that the potential tends to zero far away from a charge. Express your answer in terms of $q,d,$ and appropriate constants. What is the contribution $U_{2q}$ to the electric potential energy of the system, due to interactions involving the charge […]

Suppose you have 1.0 mol of O_2 gas. How many coulombs of positive charge are contained in the atomic nuclei of this gas?

This question explains the method to calculate the total positive charge inside the nuclei of any gas. Every gas has a different positive charge inside its nucleus and the total number of protons also differs for every gas. The number of protons is called the atomic number, which differentiates all the elements of the periodic […]

An oil pump is drawing 44kw of electric power. Find out the mechanical efficiency of the pump.

– An oil pump of density $rho$ = 860 kgm^3 with a volume flow rate of V = 0.1 m^3s is consuming 44 kW of power while it pumps the oil out with a pipe having inner diameter to be 8 cm and outer diameter to be 12 cm. Find out the mechanical efficiency of […]

A car is stopped at a traffic light. It then travels along a straight road such that its distance from the light is given by x(t) = bt^2 – ct^3 , where b = 2.40 m/s2 and c = 0.120 m/s3 (a) Calculate the average velocity of the car for the time interval t = 0 to t = 10.0 s. (b) Calculate the instantaneous velocity of the car at t=0, t = 5.0 s, and t = 10.0 s. (c) How long after starting from rest is the car again at rest?

This problem aims to familiarize us with velocity and its kinds, such as instantaneous velocity, and average velocity. The concepts required for this problem are as mentioned, but it would be helpful if you are familiar with distance and speed relations. Now the instantaneous velocity of an object is defined as the rate of change […]

A golfer hits a golf ball at an angle of 25.0 to the ground. If the golf ball covers a horizontal distance of 301.5 m, what is the balls maximum height? (hint: at the top of its flight, the balls vertical velocity component will be zero.)

This problem aims to find the maximum height of a golf ball that has been hit in a projectile manner at an angle of $25.0$ and covering a range of $305.1 m$. This problem requires the knowledge of projectile displacement formulas, which include projectile range and height. Projectile motion is the term for the movement […]

Find the tension in each cord in the figure (figure 1) if the weight of the suspended object is w.

This question aims to find the tension in the string when a body of mass with weight $w$ is suspended from it. Figure 1 shows the two formations of suspension. The question is based on the concept of tension. Tension can be defined by the force exerted by the string or cord when a body […]

In a carnival booth, you can win a stuffed giraffe if you toss a quarter into a small dish. The dish is on a shelf above the point where the quarter leaves your hand and is a horizontal distance of 2.1 m from this point. If you toss the coin with a velocity of 6.4 m/s at an angle of 60° above the horizontal, the coin will land in the dish. Ignore air resistance. What is the height of the shelf above the point where the quarter leaves your hand?

This problem aims to familiarize us with the projectile motion of an object where a coin is thrown in a dish with some horizontal velocity. This problem requires the concepts of projectile motion, momentum, and complementary angles. Now, projectile motion is a type of motion in which an object is thrown or tossed into the […]

A Cessna aircraft has a liftoff speed of 120 km/h. What minimum constant acceleration does the aircraft require if it is to be airborne after a takeoff run of 240 m?

This article aims to find the acceleration of the aircraft. The article uses the equation of kinematics. Kinematic equations are a set of equations that describe the motion of an object with constant acceleration. Kinematic equations require knowledge of derivatives, rate of change, and integrals. Kinematics equations link five kinematics variables. Displacement $(denoted : by : Delta x)$ […]

Calculate the total potential energy, in Btu, of an object that is 20 ft below a datum level at a location where g=31.7 ft/s^2 and which has mass of 100lbm.

The main objective of this question is to find the total potential energy for an object in British thermal unit Btu. This question uses the concept of Potential energy. Potential energy is indeed the power that an object can store due to its position in relation to other things, internal tensions, electric charge, or even […]

A dockworker applies a constant horizontal force of 80.0 N to a block of ice on a smooth horizontal floor. The frictional force is negligible. The block starts from rest and moves 11.0 m in 5.00 s.

Find the total mass occupied by the block of ice. If the worker quits moving at the end of 5s, how long does the block move in the next 5s? This problem aims to familiarize us with the applied force and the acceleration of a moving body. The concepts required to solve this problem are from […]

If a tank holds 5000 gallons of water, which drains from the bottom of the tank in 40 minutes.

After time t, the following is the relation that represents the volume V of water that remains in the tank as per Torricelli’s Law.[{5000left(1-frac{t}{40}right)}^2=V, where 0le tle 40] As the water is draining from the tank, calculate its rate after (a)5min and (b)10min. Also, find the time at which the rate of water draining from the tank […]

A piano has been pushed to the top of the ramp at the back of a moving van. The workers think it is safe, but as they walk away, it begins to roll down the ramp. If the back of the truck is 1.0 m above the ground and the ramp is inclined at 20°, how much time do the workers have to get to the piano before it reaches the bottom of the ramp?

This article aims to find the time it takes the workers to reach the piano before it reaches the bottom of the ramp. This article uses the concept of determining the acceleration due to gravity and the length of the ramp. Gravitational acceleration is the acceleration gained by an object due to the force of gravity. Its SI unit is $ […]

The velocity function (in meters per second) is given for a particle moving along a line.

[ v(t) = 3t -8, 0 leq t leq 3 ] (a) Find the displacement. (b) Find the distance traveled by the particle during the given time interval. The aim of the question is to understand how to calculate the displacement and the distance covered by the moving particle in the given velocity and the […]

The Otto-cycle engine in a Mercedes-Benz SLK230 has a compression ratio of 8.8.

Find the ideal efficiency of the heat engine. Utilize $gamma = 1.40$. The Dodge Viper GT2 engine has a compression ratio of $9.6$. With this increase in the compression ratio, how much does the ideal efficiency increase? This problem aims to familiarize us with ratios and efficiency. The concept required to solve this problem is […]

The speed of sound in air at 20 C is 344 m/s

– In milliseconds, how long does it take for a sound wave to vibrate at a frequency at 784 Hz, or the pitch of the G5 on a piano? – What’s the wavelength of an acoustic source one octave greater than the uppermost note? The main objective of this question is to calculate the time […]

Compute the reactance of a 0.450 H inductor at the frequency of 60.0 Hz. Compute the reactance of a 2.50 microfarad capacitor at the same frequencies.

The aim of this question is to develop an understanding of the reactance of capacitors and inductors. It also covers the concept of the resonance frequency. The reactance of an inductor against the flow of alternating current can be computed using the following formula: [ X_{ L } = omega L ] The reactance of […]

A juggler throws a bowling pin straight up with an initial speed of 8.20 m/s. How much time elapses until the bowling pin returns to the juggler’s hand?

The aim of this question is to understand how to implement and apply kinematic equations of motion. Kinematics is the branch of physics dealing with objects in motion. Whenever a body moves in a straight line, then the equations of motion can be described by the following formulae: [ v_{ f } = v_{ i […]

Two snowcats in antarctica tow a housing unit to a new location at McMurdo Base, Antarctica. The sum of the forces Fa and Fb exerted on the unit by the horizontal cables is parallel to the line L. Determine Fb and Fa + Fb.

[ F_a = 4000 N ] – The angle between Fa and line L is $theta_a = 45^{circ}$. – The angle between Fb and line L is $theta_b = 35^{circ}$. The question aims to find the 2nd force exerted on the housing unit by a snowcat in Antarctica, and the sum of both forces’ magnitude […]

To throw a discus, the thrower holds it with a fully outstretched arm. Starting from rest, he begins to turn with a constant angular acceleration, releasing the discuss after making one complete revolution. The diameter of the circle in which the discus moves is about 1.8 m. If the thrower takes 1.0 s to complete one revolution, starting from rest, what will be the speed of the discus at release?

The main objective of this question is to find the speed of the disc when it is released. This question uses the concept of circular motion. In a circular motion, the motion direction is tangential and constantly changing, but the velocity is constant.The force necessary to vary the velocity is always perpendicular to the motion […]

Find the work W done by the force F in moving an object from a point A in space to a point B in space is defined as W = F.. Find the work done by a force of 3 newtons acting in the direction 2i + j +2k in moving an object 2 meters from (0, 0, 0) to (0, 2, 0).

The aim of this question is to develop a concrete understanding of the key concepts related to vector algebra such as magnitude, direction, and the dot product of two vectors in cartesian form. Given a vector $ vec{ A } = a_1 hat{ i } + a_2 hat{ j } + a_3 hat{ k } […]

A spherical hot air balloon is initially filled with air at 120 kPa and 20 degree Celsius with a velocity of 3 m/s through a 1 m diameter opening. How many minutes will it take to inflate this balloon to a 17 m diameter when the pressure and temperature of the air in the balloon remain the same as the air entering the balloon?

The aim of this question is to understand the rate of change in volume or rate of change of mass. It also introduces the basic formulae of volume, area, and volumetric flow rate. The mass flow rate of a fluid is defined as the unit mass passing through a point in unit time. It can […]

If a car takes a banked curve at less than the ideal speed, friction is needed to keep it from sliding toward the inside of the curve (a real problem on icy mountain roads). (a) Calculate the ideal speed to take a 80 m radius curve banked at 15.0. (b) What is the minimum coefficient of friction needed for a frightened driver to take the same curve at 25.0 km/h?

This problem aims to find the velocity of a car running on a curved surface. Also, we are to find the coefficient of friction between the car’s tires and the road. The concept required to solve this problem is related to introductory dynamic physics, which includes velocity, acceleration, coefficient of friction, and centripetal force. We […]

A plane flying horizontally at an altitude of 1 mi and a speed of 500 mi/h passes directly over a radar station. Find the rate at which the distance from the plane to the station is increasing when it is 2 mi away from the station.

This question aims to develop an understanding of the Pythagorean theorem and basic rules of differentiation. If we have a right triangle, then according to the Pythagorean theorem the relation between its different sides can be described mathematically with the help of the following formula: [ ( hypotenuse )^{ 2 } = ( base )^{ […]

A jet plane lands with a speed of 100 m/s and can accelerate at a maximum rate of 7m/s^2 as it comes to rest. Can this plane land on a small tropical island airport where the runway is 0.900 km long?

The question aims to find if a plane can land on a small tropical island if the runway is shorter than a kilometer. The question depends on the concept of 3rd equation of motion. The 3rd equation of motion yields final velocity given a uniform acceleration and initial velocity over a given distance. The formula for […]

The Humber bridge in England has the World’s longest single span, 1410 m .

This guide aims to find the change in length of the steel deck of the span when the temperature increases from – 5.0 ° C to 18 ° C. The Humber Bridge in England has the longest single span of 1410 m in the world. Linear thermal expansion is defined as the increase in the […]

An open tank has a vertical partition and on one side contains gasoline with a density p= 700 kg/m^3 at a depth of 4m. Arectangular gate that is 4 m high and 2 m wide and hinged at one end is located in the partition. Water is slowly added to the empty side of the tank. At what depth, h, will the gate start to open?

This question aims to determine the depth of a tank given the density of liquid, height, and width of the tank. This article uses the concept of force exerted by the liquid on the walls of the tank. The magnitude of hydrostatic force applied to the immersed surface is given by: [F = P_{c}A ] Expert Answer The depth […]

An iceberg (specific gravity 0.917) floats in the ocean (specific gravity 1.025 ). What percent of the volume of the iceberg is under water?

This problem works to familiarize us with the weight of objects underwater. The concept required to solve this problem includes the force density formula and the Buoyant force. Buoyancy, more commonly known as upthrust, is an upward force exercised by a fluid that resists the weight of a partly or fully submerged object. In simple […]

An airplane flies at an altitude of 5 miles toward a point directly over an observer.

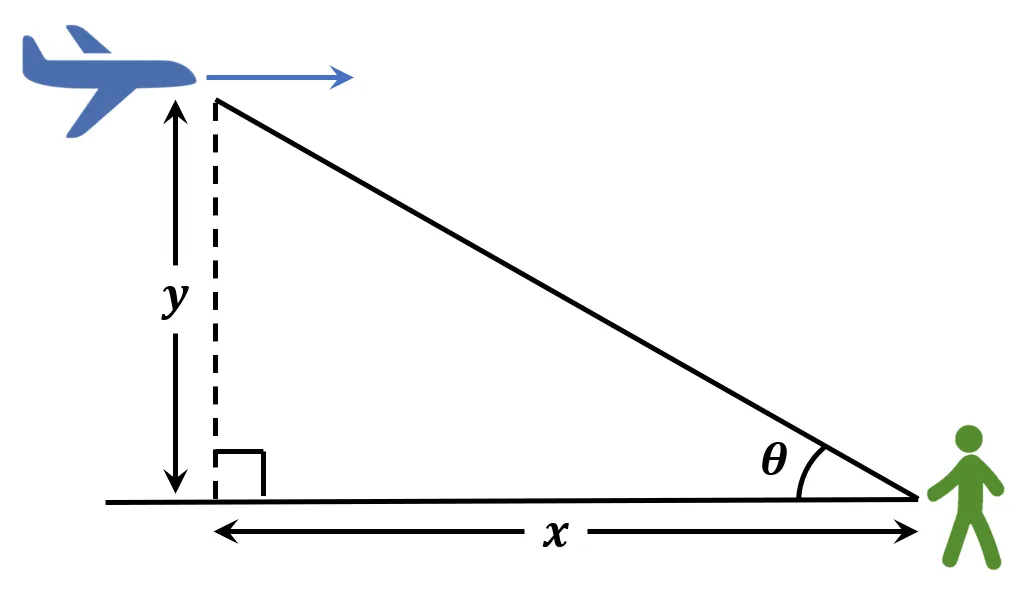
An airplane having a speed of $600$ miles per hour is flying at an altitude of $5$ miles in the direction of an observer as per the figure. What will be the rate at which the angle of elevation is changing when the angle of observation $theta$ is: $a)$ $theta = 30°$ $b)$ $theta = […]

In getting ready to slam-dunk the ball, a basketball player starts from rest and sprints to a speed of 6.0 m/s in 1.5 s. Assuming that the player accelerates uniformly, determine the distance he runs.

This question aims to find the distance a basketball player runs from rest and moves with speed 6.0 m/s. The article uses an equation of motion to solve for unknown values. Equations of motion are mathematical formulas that describe a body’s position, velocity, or acceleration relative to a given frame of reference. If the position of […]

A horizontal rope is tied to a 50 kg box on frictionless ice. What is the tension in the rope if a. The box is at rest? b. The box moves at a steady 5.0 m/s? c. The box has v_{x}=5.0m/s and a_{x}=5.0m/s^2.

The question aims to find the tension in a rope having some weight in different conditions when the box is at rest, moving with constant velocity, and moving with some value of speed and acceleration. Tension is defined as the force transmitted by a rope, string, or wire when pulled by forces acting from opposite sides. The pulling force is directed […]

A high-speed flywheel in a motor is spinning at 500 rpm when a power failure suddenly occurs. The flywheel has mass 40.0 kg and diameter 75.0 cm. The power is off for 30.0 s, and during this time the flywheel slows due to friction in its axle bearings. During the time the power is off, the flywheel makes 200 complete revolutions.

At what rate is the flywheel spinning when the power comes back on? How long after the beginning of the power failure would it have taken the flywheel to stop if the power had not come back on, and how many revolutions would the wheel have made during this time? The question aims to find […]

A nozzle with a radius of 0.250 cm is attached to a garden hose with a radius of 0.750 cm. The flow rate through hose and nozzle is 0.0009. Calculate the speed of the water.

In the hose. In the nozzle. This problem aims to familiarize us with the relationship between flow rate and speed of a liquid from a specific cross-sectional area. The concept required to solve this problem is as mentioned, but it would be a plus if you are familiar with Bernoulli’s principle. Now the flow rate […]

A mountain lion can make a leap 10.0 m long, reaching a maximum height of 3.0 m. What is the speed of the mountain lion just as it leaves the ground?

The aim of this question is to utilize the equations of motion for solving 2D motion-related problems. The speed is the rate of change of distance s with respect to time t: […]

Two protons are aimed directly toward each other by a cyclotron accelerator with speeds of 3.50 * 10^5 m/s, measured relative to the Earth. Find the maximum electrical force that these protons will exert on each other.

This problem aims to brief the concepts of attractive and repulsive forces between two point charges having the same magnitudes. This problem requires the knowledge of field forces, Coulomb’s law, and the Law of conservation of energy, which is briefly explained in the solution below. Expert Answer Coulomb’s law states that the maximum force between […]

What is the position vector r(t) as a function of angle Θ(t). Give your answer about R, Θ(t), and the unit vectors x and y corresponding to the coordinate system.

Find $theta(t)$ at an arbitrary time t for uniform circular motion. Present the answer in terms of $omega$ and t. Find position vector r at time. Present the answer in terms of $R$ and unit vectors x and y. Find the formula for the position vector of a particle that starts with $ (that:is, (x_ […]

A block oscillating on a spring has an amplitude of 20 cm. What will the block’s amplitude be if its total energy is doubled?

The main objective of this question is to find the amplitude of the oscillating block when the total energy gets doubled.This question uses the concept of simple harmonic motion and the total mechanical energy of simple harmonic motion. The total mechanical energy of the simple harmonic motion is equal to the sum of total kinetic […]

A shopper in a supermarket pushes a cart with a force of 35.0N directed at an angle of 25 below the horizontal. The force is just sufficient to balance various friction forces, so the cart moves at constant speed.

Calculate the work done by the customer on the cart as she drives down a 50m long slide. What is the net work done on the cart? Explain. The customer goes down the next slide, moving horizontally and keeping the same speed as earlier. If the friction force doesn’t alter, would the customer’s devoted force be […]

The three masses shown in the figure are connected by massless, rigid rods. Find the moment of inertia about an axis that passes through masses B and C.

If the axis is passing through mass A in the direction perpendicular to the page, calculate its moment of inertia with the proper unit and up to two significant figures. If the axis is passing through masses B and C, calculate its moment of inertia with the proper unit and up to two significant figures. […]

Three uniform spheres are fixed at positions shown in the figure. Find the magnitude and direction of the force of gravity acting on a 0.055kg mass placed at the origin.

Figure (1): Arrangement of Bodies Where, m1 = m2 = 3.0 kg, m3 = 4.0 kg The aim of this question is to grasp the concept of Newton’s law of gravitation. According to Newton’s law of gravitation, if two masses (say m1 and m2) are placed at some distance (say d) from each other attract each other with an equal and opposite […]

At NASA’s Jet Propulsion Laboratory’s 25-foot space simulator facility, a series of overhead arc lamps can generate a light intensity of 2500 $\dfrac {W} {m ^ 2} $ on the facility floor. (This simulates the intensity of sunlight near Venus.) Find the average momentum density (momentum per unit volume) in the light at the floor.

Find the average radiation pressure (Pascal and atmospheric pressure) of: the part that completely absorbs the ground. the part that completely reflects the ground. This question aims to find the average radiation pressure. Radiation pressure is actually mechanical pressure that is exerted on any surface caused by the exchange of momentum between an object and […]

A very thin oil film (n=1.25) floats on water (n=1.33). What is the minimum width of the oil film required to produce a strong reflection for green light with 500nm wavelength.

This question aims to find the width of the oil film required for a strong reflection of green light with 500nm of wavelength. The basic concepts required for this question are reflection, refraction, and wavelength of different light colors. Refraction is the phenomenon in physics in which light changes its direction when it passes from […]

A rock climber stands on top of a 70m high cliff overhanging a pool of water. He throws stones vertically downward 1.2s apart and observes that the cause a single splash. The initial speed of the first stone was 2.5 m/s. How long after the release of the first stone does the second stone hit the water?

How long after the release of the first stone does the second stone hit the water? What was the initial speed of the second stone? What is the speed of each stone as it hits the water? This question aims to find the time of the stone as it hits the water, the initial speed […]

The diffuser in a jet engine is designed to decrease the kinetic energy of the air entering the engine compressor without any work or heat interactions. Calculate the velocity at the exit of a diffuser when air at 100 kPa and 30 C enters it with a velocity of 355m/s and the exit state is 200 kPa and 90C.

The main objective of this question is to calculate the velocity of the diffuser at the exit. This question uses the concept of energy balance. The energy balance of the system states that the energy entering the system is equal to the energy leaving the system. Mathematically, the energy balance can be represented as: [ […]

About 0.1 ev is required to break a “hydrogen bond” in a protein molecule.

Calculate the minimum frequency of photon that can break a Hydrogen bond. Calculate the maximum wavelength of a photon that can break a Hydrogen bond. The question aims to find the minimum frequency of a photon and its maximum wavelength that can break a Hydrogen Bond of a protein molecule. The concepts needed to solve […]

A bicycle with 0.80 m diameter tires is coasting on a level road at 5.6 m/s. A small blue dot has been painted on the tread of the rear tire. What is the speed of the blue dot when it is 0.80 m above the road? Also, calculate the angular speed of the tires.

This question aims to calculate for these values: the speed of the blue dot that has been painted on the tread of the rear tire when it is 0.80 m above the road, the angular speed of the tires, and the speed of the blue dot when it is 0.40 m above the road. Speed […]

A ski lift has a one-way length of 1km and a vertical rise of 200m. The ski lift which is operating at a steady speed of 10km/h and chairs are separated by 20m. Three people can be seated on each chair with the average mass of each loaded chair is 250kg

– Calculate the power needed to function the ski lift. – Calculate the power needed to accelerate this ski lift in 5 s up to the speed of its operation. The first objective of this question is to find the power required to operate the ski lift by first finding the work done as the […]

A tank of water with depth of 20.0 cm and a mirror at its bottom has a small fish floating motionless 7.0 cm under the surface of the water. (a) What is the apparent depth of the fish when viewed at normal incidence? (b) What is the apparent depth of the image of the fish when viewed at normal incidence?

This question aims to find the apparent depth of a fish when it is floating motionless in the water and also the apparent depth of its image forming in the mirror at the bottom of the tank. The concepts needed to solve this question are related to refraction in water. Refraction occurs when a light […]

What is the flea’s Kinetic Energy as it leaves the ground? A 0.50 mg flea, jumping straight up, reach a height of 30 cm if there were no air resistance. In reality, air resistance limits the height to 20 cm.

The question aims to calculate the kinetic energy of a flea whose mass is $0.50 mg$ and has attained the height of 30 cm, provided that there is no air resistance. The kinetic energy of an object is defined as the energy it has acquired due to its motion. In other terms, this can also […]

A 1500 kg car takes a 50m radius unbanked curve at 15 m/s.

– Without causing the car to skid off, calculate the friction Force action on the car while taking the turn. This question aims to find the friction force acting on the car while it is taking a turn on an unbanked curve. The basic concept behind friction force is the centrifugal force that is acting […]

Consider a vehicle moving with constant velocity v. Find the Power dissipated by form drag.

This question aims to find the power dissipated by a drag force when velocity is kept constant. Drag force is a force experienced by any object moving with a certain velocity. If objects do not experience any kind of force, then they will be moving like a breeze. Drag force quadratically increases with the velocity. […]