
This article aims to find the acceleration of the aircraft. The article uses the equation of kinematics. Kinematic equations are a set of equations that describe the motion of an object with constant acceleration. Kinematic equations require knowledge of derivatives, rate of change, and integrals. Kinematics equations link five kinematics variables.
- Displacement $(denoted \: by \: \Delta x)$
- Initial velocity $(denoted \: by \: v_{o} )$
- Final velocity $ (denoted\: by \: v_{f} )$
- Time interval $ (denoted\: by \: t) $
- Constant acceleration $ (denoted \: by \: a ) $
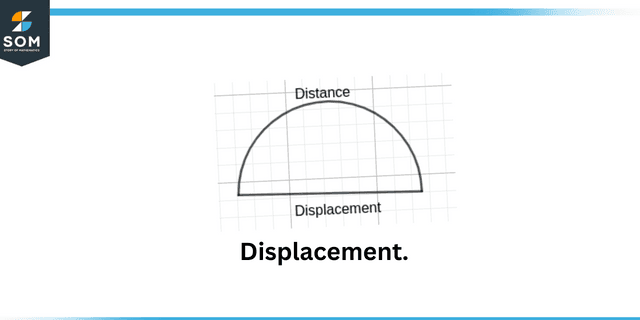
displacement.
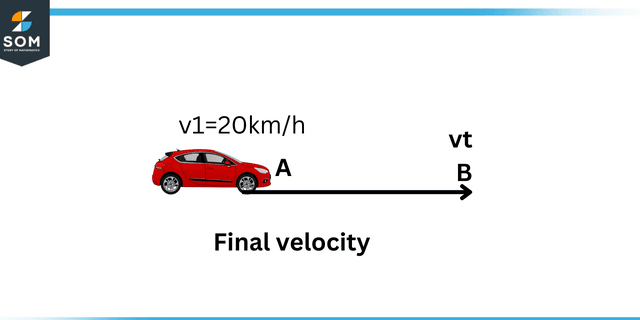
Final velocity
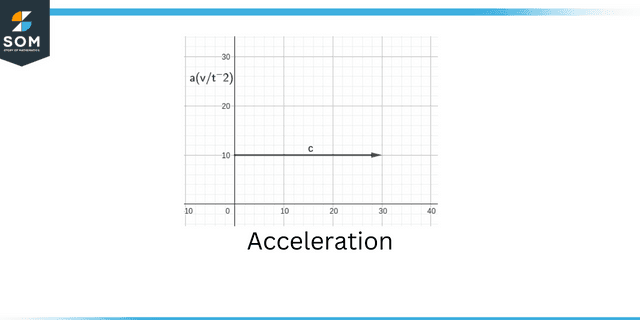
Acceleration
These are basic kinematics equations.
\[v = v_ {0} +at \]
\[ v _{f} ^ {2} = v_{i} ^ {2} + 2aS \]
\[ \Delta x = (\dfrac {v + v_{0} }{2} ) t\]
Expert Answer
Aircraft starts from rest. Therefore, the initial speed is:
\[ v _ {i}= 0.00 \:m s ^ {-1} \]
The final speed of the aircraft is:
\[ v _ {f} = 120\: kmh ^ {-1} \]
\[ = 33.3 \: ms ^ {-1} \]
Takeoff run length is:
\[\Delta x = 240\: m\]
Here, we have the initial velocity, final velocity, and displacement, so we can use the kinematic equation to calculate the acceleration as:
\[ v _{f} ^ {2} = v_{i} ^ {2} + 2aS \]
Rearranging the above equation for acceleration:
\[ a = \dfrac {v _{f} ^ {2}\: – \:v_{i} ^ {2} } {2S} \]
\[ = \dfrac {(33.3\: m s ^ {-1} ) ^ {2} – (0.00 \: m s ^ {-1}) ^ {2} } {2 \times 240m}\]
\[ = 2.3148 \: m s ^ {-2} \]
\[a = 2.32 \: m s ^ {-2} \]
The acceleration of the aircraft is $ 2.32 \: m s ^ {-2} $.
Numerical Result
The acceleration of the aircraft is $2.32 \: m s ^ {-2} $.
Example
A Cessna airplane has a take-off speed of $150\: \dfrac {km} {h}$. What minimum constant acceleration does the airplane need if it is to be in the air $250\: m$ after takeoff?
Solution
Aircraft starts from rest, therefore the initial speed is:
\[ v _{i}= 0.00 \: m s ^ {-1} \]
The final speed of the aircraft is:
\[ v_{f} = 150\: kmh ^ {-1} \]
\[ = 41.66 \: ms ^ {-1} \]
Takeoff run length is:
\[\Delta x = 250 \: m\]
Here, we have the initial velocity, final velocity, and displacement, so we can use the kinematic equation to calculate the acceleration as:
\[ v _{f} ^{2} = v_{i} ^ {2} + 2aS \]
Rearranging the above equation for acceleration:
\[ a = \dfrac {v _ {f} ^ {2}\: – \:v _ {i} ^ {2}} {2S} \]
\[ = \dfrac {(41.66\: m s ^ {-1} ) ^{2} – (0.00 \: m s ^ {-1}) ^ {2} } {2 \times 250m}\]
\[ = 2.47 \: m s ^ {-2} \]
\[a = 2.47 \: m s ^ {-2} \]
The acceleration of the aircraft is $ 2.47 \: m s ^ {-2} $.
