
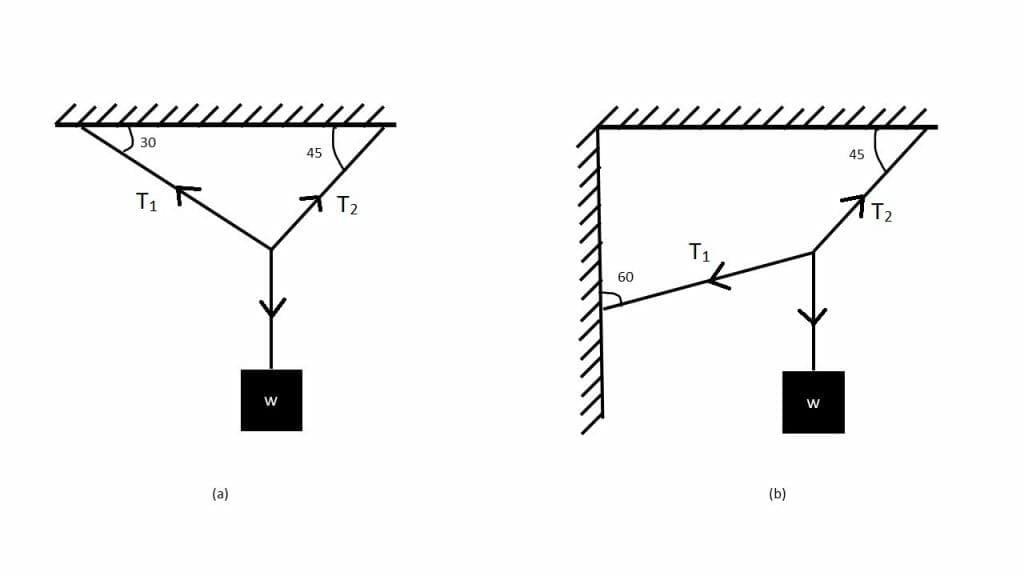
Figure 1
This question aims to find the tension in the string when a body of mass with weight $w$ is suspended from it. Figure 1 shows the two formations of suspension.
The question is based on the concept of tension. Tension can be defined by the force exerted by the string or cord when a body of the weight is suspended by it. Simple trigonometric ratios of a right-angle triangle and basic triangle geometry are also needed to solve this question. Let’s suppose a body of weight $W$ is attached to a string, and the other end of the string is attached to a fixed point. The tension $T$ in the string is given as :
\[ T = W \]
Here, the weight of the body will be downward, and tension in the string will be in the upward direction.
Expert Answer
a) In the first part of the question, we can see that the $T_1$ makes an angle of $30^{\circ}$ and $T_2$ makes an angle of $45^{\circ}$. As the weight and cord are balanced, the tension in left cord must be equal to tension in the right cord. This can be written as:
\[ T_1 \cos (30^{\circ}) = T_2 \cos(45^{\circ}) \hspace{0.4in} (1) \]
According to the definition of the tension, the forces pointing upwards are equal to the forces pointing downwards. This means that the tension in both cords pointing upward is equal to the weight of the object pointing downward. The equation can be written as:
\[ T_1 \cos (60^{\circ}) + T_2 \cos (45^{\circ}) = W \]
Calculated in equation $(1)$, the tension in the right cord is equal to the tension in the left cord. We can replace the value $T_2$ with $T_1$.
\[ T_1 \cos (60^{\circ}) + T_1 \cos (30^{\circ}) = W \]
\[ T_1 = \dfrac{2W}{1 + \sqrt{3}} \]
Putting the value of $T_1$ in equation $(1)$ to find the tension in the cord on the right side:
\[ (\dfrac{2W}{1 + \sqrt{3}}) \cos(30^{\circ}) = T_2 \cos(45^{\circ}) \]
Solving for $T_2$, we get:
\[ T_2 = \dfrac{\sqrt{6} W}{1 + \sqrt{3}} \]
b) In the second part of the question, the cord on the left side also has tension pointing downwards, same as the weight. We can write this equation in this manner:
\[ T_1 \cos(60^{\circ}) + W = T_2 \cos(45^{\circ}) \]
Here, the tension on the right side will be equal to the horizontal component of the cord on the left side.
\[ T_1 \cos(30^{\circ}) = T_2 \cos(45^{\circ}) \hspace{0.4in} (2) \]
Substituting this value of $T_1$ in the above equation to find its value, we get:
\[ T_1 \cos(60^{\circ}) + W = T_1 \cos(30^{\circ}) \]
\[ T_1 = \dfrac{2 W}{1 – \sqrt{3}} \]
Substituting this value in equation $(2)$ to get the value of $T_2$:
\[ (\dfrac{2W}{1 – \sqrt{3}}) \cos(30^{\circ}) = T_2 \cos(45^{\circ}) \]
Solving for $T_2$, we get:
\[ T_2 = \dfrac{\sqrt{6}W}{1 – \sqrt{3}} \]
Numerical Results
a) The tension in the cords in the first part of the question are given as:
\[ [T_1, T_2] = \Bigg{[}\dfrac{2W}{1 + \sqrt{3}}, \dfrac{\sqrt{6}W}{1 + \sqrt{3}}\Bigg{]} \]
b) The tension in the cords in the second part of the question are given as:
\[ [T_1, T_2] = \Bigg{[}\dfrac{2W}{1 – \sqrt{3}}, \dfrac{\sqrt{6}W}{1 – \sqrt{3}}\Bigg{]} \]
Example
Find the weight of the body if it is suspended with two strings with tension amounting to $5N$ and $10N$.
According to the definition of tension, the weight is equal to the tension in the cords. We can write this problem as:
\[ T_1 + T_2 = W \]
Substituting the values, we get:
\[ W = 5N + 10N \]
\[ W = 15N \]
The weight of the body suspended by the cords is $15N$.
