
This problem aims to find the maximum height of a golf ball that has been hit in a projectile manner at an angle of $25.0$ and covering a range of $305.1 m$. This problem requires the knowledge of projectile displacement formulas, which include projectile range and height.
Projectile motion is the term for the movement of an object flung or cast into the air, related to only the acceleration due to gravity. The object that is flung is known as a projectile, and its route is known as its course. This problem can be cracked using the equations of projectile motion with constant acceleration. As the object is covering a horizontal distance, the acceleration here must be null. Thus, we can express the horizontal displacement as:
\[ x = v_x \times t \]
Where $v_x$ is the horizontal component of the velocity and $t$ is the flight time.
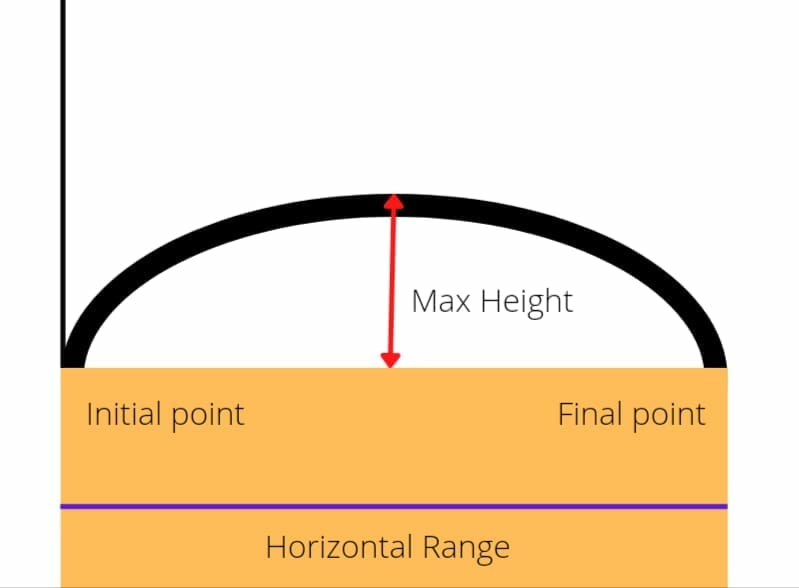
Figure 1
Expert Answer
We are given the following parameters:
$R = 301.5 m$, $R$ is the horizontal distance that the ball travels after a projectile motion.
$\theta = 25$, $\theta$ is the angle with which the ball is displaced from the ground.
The formula of vertical motion can be derived from the first equation of motion, which is given as:
$v = u + at$
where,
$v$ is the final velocity, and its value is the vertical component of the initial velocity –> $usin\theta$
$u$ is the Initial velocity = $0$
$a$ is the negative Acceleration, as the ball is moving upwards against the force of gravity = $-g$
The formula for acceleration due to gravity is $g = \dfrac{v – u}{t}$
Rearranging the above formula for value of $t$,
\[t=\dfrac{usin\theta}{g} \]
The formula for the horizontal range of Projectile motion is given:
\[R=v \times t \]
Plugging in the expressions of $v$ and $t$ gives us:
\[R=usin\theta \times \dfrac{usin\theta}{g} \]
\[ R=\dfrac{u^2 sin^2\theta}{g} \]
Now that we have our formula to compute the final velocity, we can further plug in the values to compute $u$:
\[301.5 = \dfrac{u^2 sin^2(25)}{9.8} \]
\[\dfrac{301.5 \times 9.8}{sin^2(25))} = u^2 \]
\[u^2 = 3935 m/s \]
Next, to compute the maximum height of the projectile $H$, we will use the formula as given:
\[H = \dfrac{u^2 sin^2\theta}{2g} \]
\[H = \dfrac{3935 \times sin^2(25)}{2(9.8)} \]
Numerical Result
The maximum height is calculated to be:
\[H = 35.1 m \]
Example:
A golfer hits one golf ball at an angle of $30^{\circ}$ to the ground. If the golf ball covers a horizontal distance of $400$, what is the ball’s maximum altitude?
The formula for the horizontal range of Projectile motion is given:
\[R = \dfrac{u^2 sin^2\theta}{g} \]
Now that we have our formula to compute the final velocity, we can further plug in the values to compute $u$:
\[400 = \dfrac{u^2 sin^2(30)}{9.8} \]
\[\dfrac{400 \times 9.8}{sin^2(30))} = u^2\]
\[u^2= 4526.4 m/s\]
Finally, to compute the maximum height of the projectile $H$, we will use the formula as given:
\[H=\dfrac{u^2 sin^2\theta}{2g}\]
\[H=\dfrac{4526.4 \times sin^2(30)}{2(9.8)}\]
Horizontal distance comes out to be:
\[H = 57.7 m\]
Images/mathematical drawings are created with GeoGebra
