
This question explains the method to calculate the total positive charge inside the nuclei of any gas.
Every gas has a different positive charge inside its nucleus and the total number of protons also differs for every gas. The number of protons is called the atomic number, which differentiates all the elements of the periodic table.
The positive charge on each proton is the same for every gas. The total charge will be the sum of the charge on all protons contained in the gas.
Expert Answer
The total positive charge in the nucleus of any gas is the total number of protons times the total charge contained by one proton. The total number of protons depends on the type of gas, for example, hydrogen, oxygen, chlorine, etc. Each gas has a different number of protons in its nuclei.
To calculate the total positive charge in the atomic nuclei of any gas, find the total number of atoms in the gas. It can be calculated by multiplying Avogadro’s Number $N_A$ with the total amount of gas in moles. If the gas is available in molecules like $O_2, F_2, Cl_2$, then it needs to be multiplied by 2 to calculate the correct number of atoms in the gas. The total number of protons needs to be calculated, which can be done by multiplying the atomic number of gas with the total number of atoms calculated before. Now we can calculate the charge by multiplying the charge on one proton by the total number of protons.
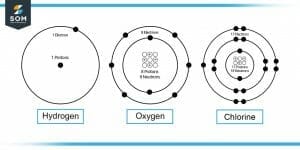
Figure-1 : Hydrogen, Oxygen and Chlorine Molecules
Suppose we need to find the total positive charge in 1 mole of $O_2$ gas. Now we need to find the total number of atoms in 1 mole of $O_2$ gas. $O_2$ has 2 atoms in each molecule, so we would need to incorporate this in our calculations.
Amount of Gas, n = 1 mols
Atoms in 1 molecule, m = 2 atoms
Protons in 1 atom, P = 8
Charge on 1 Proton, e = 1.6 x $10^{-19}$ C
Avogadro’s Constant, N_A = 6.022 x $10^{23}$
Total Number of Atoms, N = n x m x $N_A$
N = 1 x 2 x 6.022 x $10^{23}$
N = 1.2 x $10^{24}$
Total Number of Protons, $T_p$ = N x P
$T_p$ = 1.2 x $10^{24}$ x 8
$T_p$ = 9.6 x $10^{24}$
Numerical Result
Total Charge, Q = Tp x e
Q = 9.6 x $10^{24}$ x 1.6 x $10^{-19}$
Q = 1.54 x $10^6$ C
Example
Suppose we need to find the total positive charge in Fluorine(F) gas nuclei. We take only one atom of F gas to calculate the positive charge in its nucleus.
Atomic Number of Fluorine, Z = 9
Charge on 1 Proton, e = 1.6 x $10^{-19}$ C
Total Charge, Q = Z x e
Q = 9 x 1.6 $10^{-19}$ C
Q = 1.44 x $10^{-18}$ C
The total charge in the atomic nuclei of Fluorine gas is $1.44 \times 10^{-18} C$. As we have the positive atomic charge of one atom of F gas, we can now calculate the positive charge for any given amount of gas. For example, if we are given $1$ mol of F gas, and we need to find the total positive charge, we simply need to find the total number of atoms in 1 mol of F gas and multiply it with the charge in one atom.
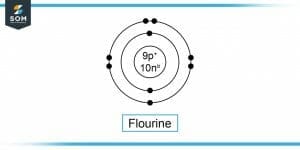
Figure-2 : Flourine Molecule
Amount of Gas, n = 1 mols
Avogadro’s Constant, $N_A$ = 6.022 x $10^{23}$
Total Number of Atoms, N = n x m x $N_A$
N = 1 x 6.022 x $10^{23}$
N = 6.022 x $10^{23}$
Total Charge, $Q_t$ = N x Q
$Q_t$ = 6.022 x $10^{23}$ x 1.44 x $10^{-18}$ C
$Q_t$ = 8.7 x $10^5$ C
