
This question aims to find the cylindrical and spherical coordinates of the plane z = x.
This question is based on the concept of coordinate systems from calculus. Cylindrical and spherical coordinate systems are expressed in the cartesian coordinate systems. A spherical object like a sphere of a ball is best expressed in a spherical coordinate system while cylindrical objects like pipes are best described in the cylindrical coordinate system.
Expert Answer:
The plane z =x is a plane that lies in the xz-plane in the cartesian coordinate system. The graph of plane z=x is shown in Figure 1 and it can be seen that the y-component of the graph is zero.
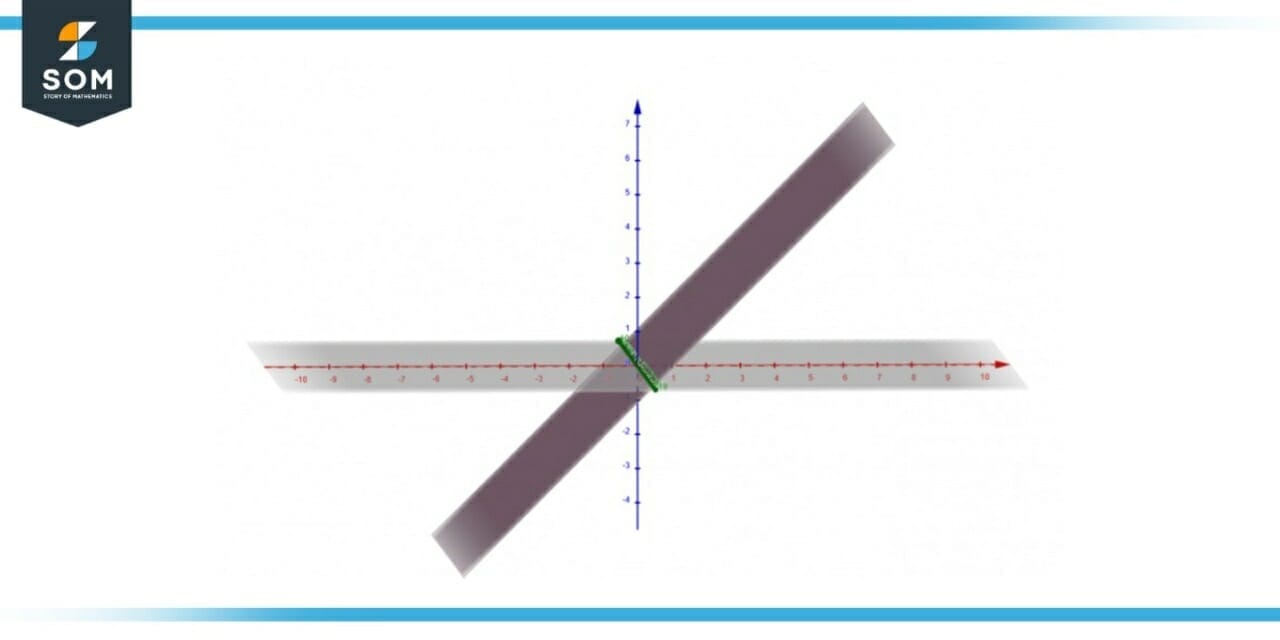
Figure-1 : Cartesian Coordinate System
We can express this plane in spherical and cylindrical coordinates using their derived formulas.
1) Cylindrical Coordinates are given by:
\[ (x, y, z) = (r \cos \theta, r \sin \theta, z) \quad 0 \leq \theta \leq 2\pi \]
Where,
\[ r = \sqrt{x^2 + y^2} \quad r \geq 0 \]
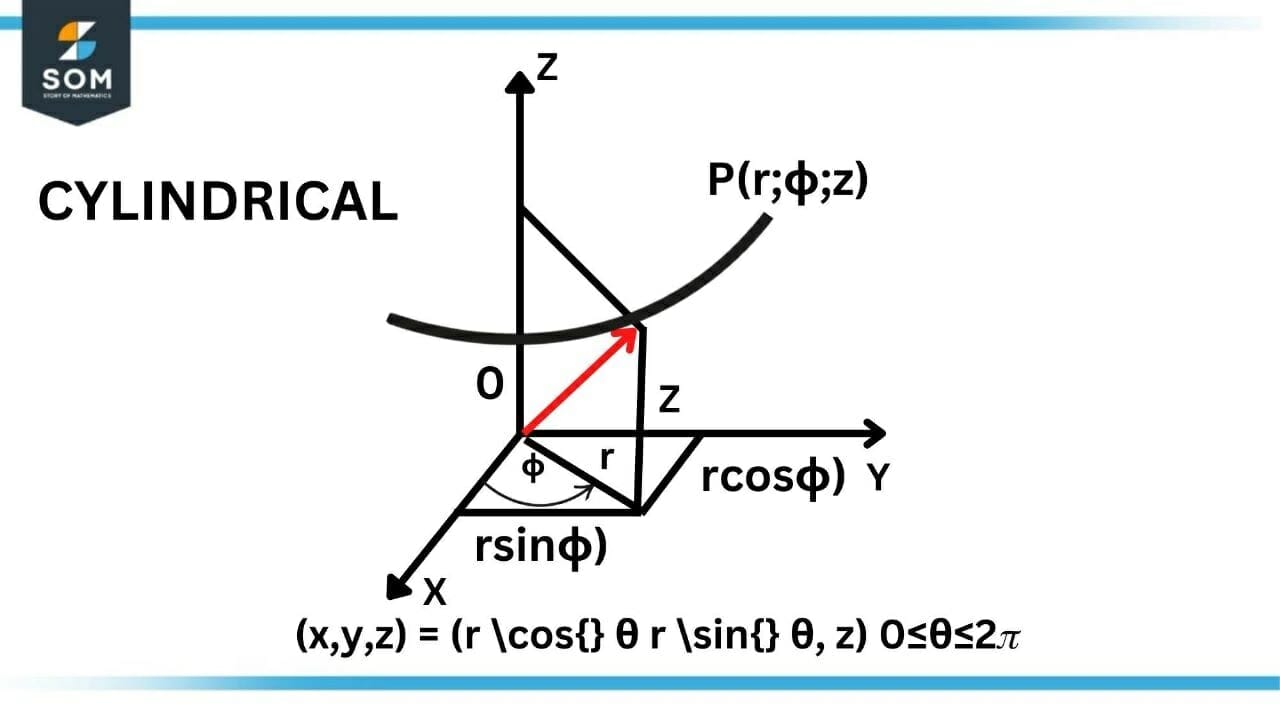
Figure-2 : Cylindrical Coordinate System
Given,
\[ z = x \]
So the equation becomes,
\[ (x, y, z) = (r \cos \theta, r \sin \theta, r \cos \theta) \]
2) Spherical Coordinates are given by:
\[ (x, y, z) = (\rho \sin \phi \cos \theta, \rho \sin \phi \sin \theta, \rho \cos \phi) \quad \rho \geq 0, 0 \leq \theta \leq 2\pi, 0 \leq \phi \leq \pi \]
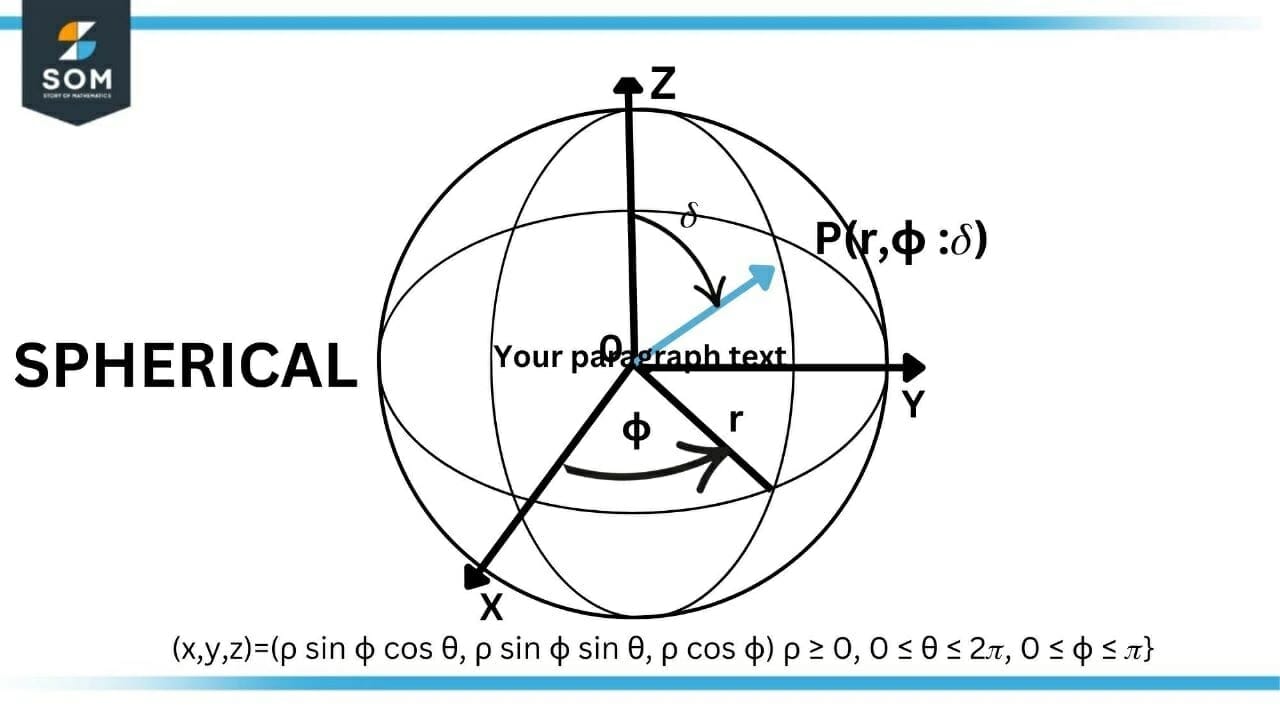
Figure-3 : Spherical Coordinate System
Given,
\[ z = x \]
\[ \rho \cos \phi = \rho \sin \phi \cos \theta \]
\[ \dfrac{\cos \phi}{\sin \phi} = \cos \theta \]
\[ \cot \phi = \cos \theta \]
\[ \theta = \arccos (\cot \phi) \]
By substituting the values we get,
\[ (x, y, z) = (\rho \sin \phi \cos (\arccos (\cot \phi)), \rho \sin \phi \sin (\arccos (\cot \phi)), \rho \cos \phi) \]
Simplifying by using trigonometric identities, we get:
\[ (x, y, z) = (\rho \cos \phi, \rho \sin \phi \sqrt{1 – \cot^{2} \phi}, \rho \cos \phi) \]
Numerical Results:
Cylindrical Coordinates,
\[ (x, y, z) = (r \cos \theta, r \sin \theta, r \cos \theta) \]
Spherical Coordinates,
\[ (x, y, z) = (\rho \cos \phi, \rho \sin \phi \sqrt{1 – \cot^{2} \phi}, \rho \cos \phi) \]
Example:
Convert $(5, 2, 3)$ cartesian coordinates into cylindrical and spherical coordinates.
Cylindrical Coordinates are given by,
\[ (x, y, z) = (r \cos \theta, r \sin \theta, z) \]
Here,
\[ r =5.38 \]
And,
\[ \theta = 21.8^{\circ} \]
By substituting the values, we get,
\[ (x, y, z) = (20.2, 8.09, 3) \]
Spherical Coordinates are given by,
\[ (x, y, z) = (\rho \sin \phi \cos \theta, \rho \sin \phi \sin \theta, \rho \cos \phi) \]
We calculated the values of $r$ and $\theta$ above and now we calculate $\rho$ and $\phi$ for spherical coordinates.
\[ \rho = r^2 + z^2 \]
\[ \rho = 6.16 \]
We know that $\phi$ is the angle between $\rho$ and $z-axis$, and by using geometry we know that $\phi$ is also the angle between $\rho$ and the vertical side of the right-angled triangle.
\[ \phi = 90^{\circ} – \theta \]
\[ \phi = 68.2^{\circ} \]
By substituting the values and implying, we get:
\[ (x, y, z) = (5.31, 2.12, 2.28) \]
Images/Mathematical drawings are created with Geogebra.
