
- An airplane having a speed of $600$ miles per hour is flying at an altitude of $5$ miles in the direction of an observer as per the figure. What will be the rate at which the angle of elevation is changing when the angle of observation $\theta$ is:
$a)$ $\theta = 30°$
$b)$ $\theta = 75°$
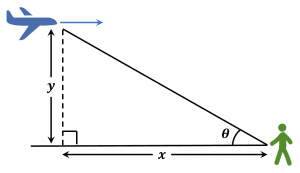
As we know, if an object moves horizontally at a certain and constant height with reference to a base point, the angle of the object with respect to the baseline continuously changes. If the object is moving away from the observation point, the angle decreases. If the object is moving towards the observation point, the angle increases.
Expert Answer
Given as:
Altitude of airplane $y=5mi$
Horizontal distance of the observer $=$ $x$
Speed of the plane $=$ $-600$ $\dfrac{mi}{h}$ as it is towards the observer.
Using trigonometric equation:
\[\tan{\theta=\frac{y}{x}}\]
By substituting the given values:
\[\tan{\theta}=\ \frac{5\ mi}{x}\]
As speed is defined as rate of change of distance $\dfrac{dx}{dt}$, so
\[\frac{dx}{dt}=\ -600\ \frac{mi}{h}\]
Taking derivative of $ \tan{\theta}=\ \dfrac{5\ mi}{x} $ with respect to time $t$.
\[\frac{d}{dt}\ (\ \tan{\theta}=\ \frac{5\ mi}{x}\ )\]
We get,
\[\sec^2{(\theta)}\ \ \frac{(d\theta)}{dt}=\ \frac{-5\ mi}{x^2}\ \times\ \frac{dx}{dt}\ \]
\[\frac{d\theta}{dt}\ =\ \frac{-5\ mi}{\sec^2{\left(\theta\right)}\ \times\ x^2}\ \times\ \frac{dx}{dt}\ \ \]
\[\frac{d\theta}{dt}\ =\ \frac{-5\ mi\ \times\ \cos^2{\left(\theta\right)}\ }{\ x^2}\ \ \times\ (-\ 600\frac{\ mi}{h}\ )\]
Now solving $ \tan{\theta}=\ \dfrac{5\ mi}{x} $ for $x$
\[\tan{\theta}=\frac{5\ mi}{x}\]
\[x\ =\frac{5\ mi}{\tan{\theta}}\]
Putting the value of $x$
\[\frac{d\theta}{dt}\ =\ \frac{-5\ mi\ \times\ \cos^2{\left(\theta\right)}\ }{\ {(\ \dfrac{5\ mi}{\tan{\theta}}\ \ )}^2}\ \ \times\ (-\ 600\frac{\ mi}{h}\ \ )\]
\[\frac{d\theta}{dt}\ =\ \frac{-5\ mi\ \times\ \cos^2{\left(\theta\right)}\ }{(25\ {\rm mi}^2)\ {(\ \dfrac{1}{\tan{\theta}}\ \ )}^2}\ \ \times\ (-\ 600\frac{\ mi}{h}\ \ )\]
Simplifying the equation and cancelling $ {\rm mi}^2 $,
\[\frac{d\theta}{dt}\ =\ \frac{-1\ \times\ \cos^2{\left(\theta\right)}\ }{5\ \ {(\ \dfrac{1}{\tan{\theta}}\ \ )}^2}\ \ \times\ (-\ 600\ h^{-1}\ \ )\]
As $\dfrac{1}{\tan{\theta}}\ =\cot{\theta}$
\[\frac{d\theta}{dt}\ =\ \frac{-1\ \times\ \cos^2{\left(\theta\right)}\ }{5\ \ {(\ \cot{\theta}\ \ )}^2}\ \ \times\ -\ (600\ h^{-1}\ \ )\]
\[\frac{d\theta}{dt}\ =\ 120\ \frac{\ \ \cos^2{\left(\theta\right)}\ }{\ \ {(\ \cot{\theta}\ \ )}^2}\ \ h^{-1}\ \ \]
As $\cot{\theta}\ =\ \dfrac{\cos{\theta}}{\sin{\theta}}$
\[ \frac{d\theta}{dt}\ =\ 120\ \dfrac{\ \ \cos^2{\left(\theta\right)}\ }{\ \ {(\ \cot{\theta}\ \ )}^2}\ \ h^{-1}\ \ \]
\[ \frac{d\theta}{dt}\ =\ 120\ \times\sin^2{(\ \theta\ )}\ \ h^{-1}\ \ \]
Numerical Results
$a)$ For $ \theta\ =\ 30° $
\[ \frac{d\theta}{dt}\ =\ 120\ \times\sin^2{(\ 30°\ )}\ \ h^{-1}\ \ \]
\[ \frac{d\theta}{dt}\ =\ \frac{30°}{h} \]
$b)$ For $ \theta\ =\ 75° $
\[ \frac{d\theta}{dt}\ =\ 120\ \times\sin^2{(\ 75\ )}\ \ h^{-1}\ \ \]
\[ \frac{d\theta}{dt}\ =\ \frac{111.96°}{h} \]
Example:
For the above question, find the rate at which the angle $\theta$ is changing when the angle is $\dfrac{\pi}{4}$, altitude $4$ miles and speed $400$ miles per hour.
\[ \tan{\theta}=\ \frac{4\ mi}{x} \]
\[ \frac{d\theta}{dt}\ =\ \frac{-4\ mi\ \times\ \cos^2{\left(\theta\right)}\ }{\ {(\ \dfrac{4\ mi}{\tan{\theta}}\ \ )}^2}\ \ \times\ (-\ 400\frac{\ mi}{h}\ \ )\]
\[ \frac{d\theta}{dt}\ =\ 100\ \times\sin^2{(\ \theta\ )}\ \ h^{-1}\ \ \]
\[ \frac{d\theta}{dt}\ =\ 100\ \times\sin^2{(\ \dfrac{\pi}{4}\ )}\ \ h^{-1}\ \ \]
\[ \frac{d\theta}{dt}\ =\ \frac{50°}{h} \]
Image/Mathematical drawings are created in Geogebra.
