
This question aims to determine the depth of a tank given the density of liquid, height, and width of the tank. This article uses the concept of force exerted by the liquid on the walls of the tank.

Density of liquid
Force
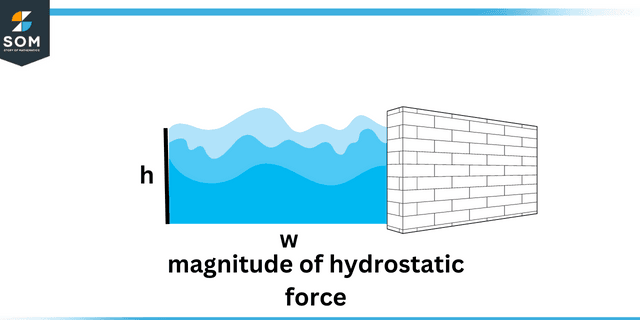
The magnitude of hydrostatic force applied to the immersed surface is given by:
\[F = P_{c}A \]
Magnitude of hydrostatic force
Expert Answer
The depth of water that will cause the gate to open can be solved by adding the forces acting on wall to the hinge. The forces acting on the wall are weight and hydrostatic due to water and gasoline.
The $\gamma $ for the water is given as:
\[\gamma = 9.80 \dfrac { kN }{m ^ {3}} \]
The specific gravity of gasoline can be solved by multiplying its density by the acceleration due to gravity, which equals $9.81 \dfrac{m}{s^{2}}$.
\[\gamma_{gas} = p_{gas} \times g \]
\[ =700 \dfrac{kg}{m^{3}} \times 9.81 \dfrac{m}{s ^ {2}}\]
\[ = 6867 \dfrac{N}{m^{3}} \]
\[ = 6.87 \dfrac{kN}{m^{3}} \]
Hydrostatic force on gate can be solved using the formula $ F_{R} = \gamma h_{c} A $ where $ \gamma $ is the specific weight of liquid, $h_{c} $ is the centroid of gate with liquid and $ A $ is area of the gate with liquid.
The hydrostatic force exerted by the gasoline is calculated as:
\[ F_{R1} = \gamma _{gas} h_{c} A \]
\[ = 6.87 \dfrac{kN}{m^{3}} (\dfrac {4m}{2}) (4m \times 2m ) \]
\[ = 109.92 kN \]
The hydrostatic force exerted by the water is calculated as:
\[ F_{R1} = \gamma _{water} h_{c} A \]
\[F_{R2} = 9.80 \dfrac { kN }{m^{3}} (\dfrac {h}{2}) (h \times 2m) \]
\[F_{R2} = 9.80 h^{2} \dfrac { kN }{m^{3}} \]
The location of hydrostatic force for rectangular plane surfaces can be found $\dfrac {1}{3} $ height of the liquid from the base.
\[ F_{R1} \times \dfrac{1}{3} .4m = F_{R2} \times \dfrac{1}{3} .h \]
\[ 109.92 kN\times \dfrac{1}{3} .4m = 9.80 h^{2} \dfrac { kN }{m^{3}} \times \dfrac{1}{3} .h \]
\[ 1146.56 kNm = 3.27 h^{3} \dfrac { kN }{m^{2}} \]
\[ h^{3} = 44.87 m^{3} \]
\[ h=3.55m \]
Numerical Result
The depth $ h $ of the tank is $3.55m$.
Example
A tank has a vertical partition and on one side contains gasoline with a density $p = 500 \dfrac {kg}{m^{3}}$ at a depth of $6\:m$. A rectangular gate that is $6\:m$ high and $3\: m$ wide and hinged at one end is located in the partition. Water is added to the empty side of the tank. At what depth, h, will the gate start to open?
Solution
The $\gamma $ for the water is given as:
\[\gamma = 9.80 \dfrac { kN }{m ^ {3}} \]
\[\gamma_{gas} = 4.9\dfrac{kN}{m ^ {3}} \]
The hydrostatic force exerted by the gasoline is calculated as:
\[F_{R1} = 4.9 \dfrac{kN}{m ^ {3}} (\dfrac {6m}{2}) (6m \times 3m ) \]
\[ = 264.6 kN \]
The hydrostatic force exerted by the water is calculated as:
\[F_{R2} = 14.7 h ^ {2} \dfrac { kN }{m ^ {3}} \]
The height of the tank is calculated as:
\[ h =4.76m \]
