JUMP TO TOPIC
 The “per” in mathematics means “for each” or “for every” and it is used to show a ratio between two quantities or elements.
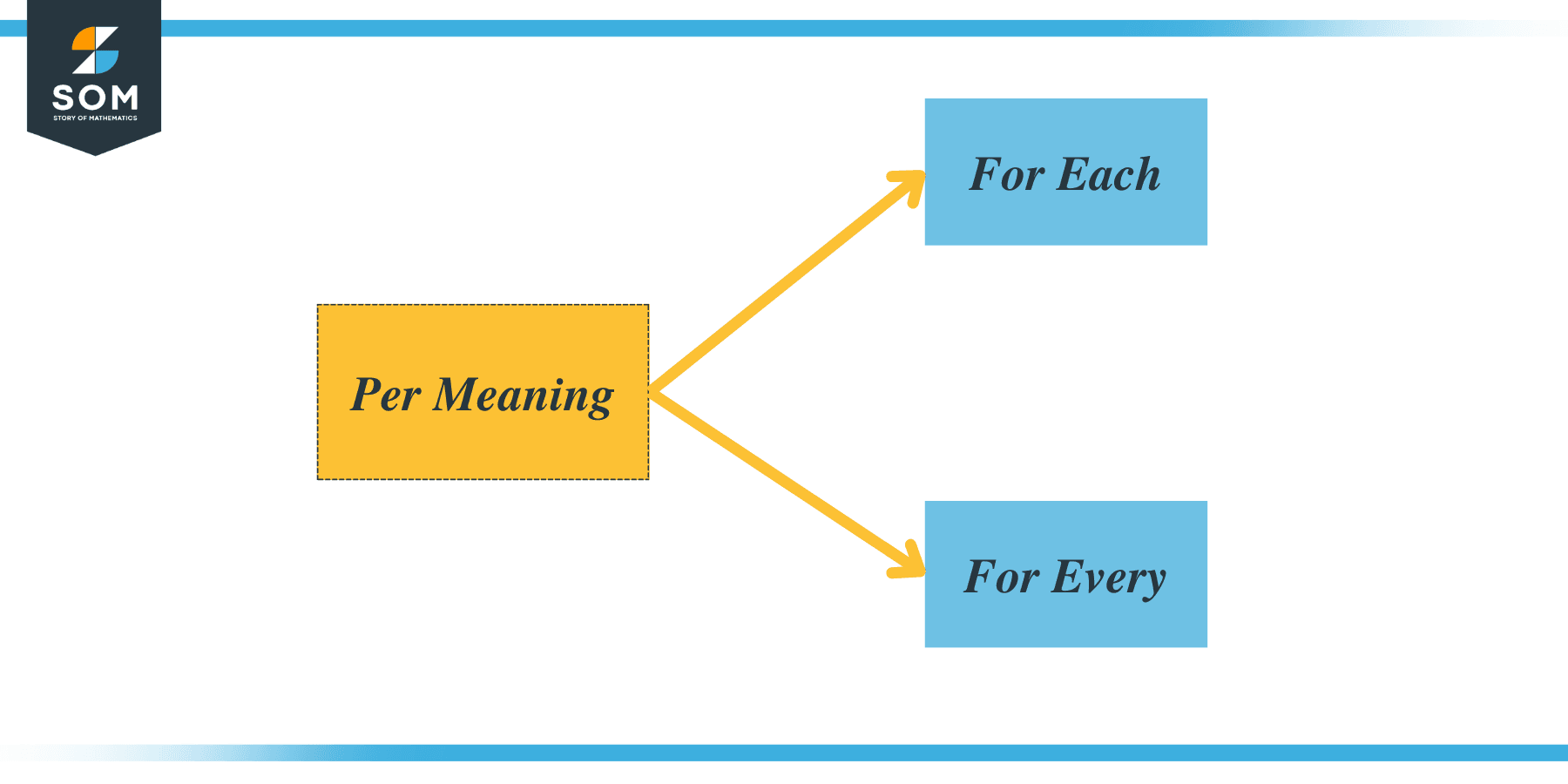
The “per” in mathematics means “for each” or “for every” and it is used to show a ratio between two quantities or elements.
The term per is generally used when we want to compare two quantities, with one as a numerator and the second as a denominator. For example, when we talk about acceleration, we are actually talking about velocity per time, so we are monitoring change in velocity with respect to time and acceleration is said to be a change in velocity per time.
What Is Meant by Per in Math?
The word per in math means “for every” or “for each,” and it is generally used to compare one quantity with respect to another in the form of a ratio. Therefore, the answer to the questions “What does per mean in math?” or “What does for each mean in math?” is the same — it means for every, and it is represented as a ratio; hence it is also taken as a division of two quantities.
Let us study an example; if a car is moving at a speed of $100$ miles per hour, it means that the car covers a distance of $100$ miles in an hour. We can use this information to calculate other information such as what will be the overall distance covered by the car in $4$ hours? If the car covers 100 miles per hour, then it will cover $400$ miles in $4$ hours.
As you can see, the term “per” is mainly used to compare different quantities in the form of a ratio. If we are dealing with rational fractions, say $\dfrac{100}{13}$, we will say $100$ is divided by $13$, or it is a ratio of $100$ to $13$, so division is basically a ratio, but it can be done for any number. We do not say $100$ per $13$, but we take the percentage of a number, and that percentage can further be used to calculate other data.
Fields Where Per is Used
The word per has been extensively used in the field of economics and accounting, especially when dealing with interest rates. For example, a firm charges $5\%$ interest per annum on the loan. This means that you will be charged 5 percent of the loan you took on an annual basis.
Similarly, if the firm charges $5\%$ interest per quarter, then you will have to pay the interest after every $3$ months. So the word per actually means “for each or for every.” Do not confuse it with simple division.
Per is used to compare quantities, and it is represented in ratio form. The comparison between the quantities is used to know available information between the quantities, and it is also helpful in the calculation of future values of the given quantities.
Per In Math Examples
Let us now discuss per in math examples and various questions related to them.
Question 1: What does per mean in math, multiply or divide?
Solution:
Per is related to division. The word per means for each or for every, and it is represented as a ratio, so it is more of a division and certainly not a multiplication process.
For example, if a student writes $250$ words per hour, then it will be written as Number of words = $\dfrac{250}{1 hour}$.
Question 2: What does per mean in math, add or subtract?
Solution:
Per is not related to either of them.
Question 3: What does per hour mean in math?
Solution:
Per hour mean $\dfrac{1}{hour}$, so if you run 2KM in 1 hour, it will be written as $2 \dfrac{KM}{hour}$
Example 1: If Allan runs $10$ kilometers in $1$ hour, find out the distance covered by Allan in $2$ hours.

Solution:
We know Allan covers 10 kilometers in 1 hour, so in 2 hours’ time, he will cover $10 + 10 = 20$ kilometers.
Example 2: If 1 unit of the electricity bill is given as $1$ KW per hour, then calculate the total unit consumption of a household for a single day.
Solution:
We know 1 unit consists of $1$ KW per hour, and we also know that in a single day, there are $24$ hours, so the total energy consumption in a single day is $24$ KW per hour. Hence, the total number of units utilized in a single day is $24$ units.
Example 3: William has taken a loan of $100,000$ dollars for a period of $3$ years from a firm with a $10\%$ interest per annum. What will be the overall amount of interest paid by William at the end of the third year?
Solution:
We can solve the question by using the simple interest formula I = p.r.t, but we will simply solve by describing it through the meaning of per. William has taken a loan of 100,000 dollars so the annual interest paid by William will be $= 100,000 \times 0.05 = 5000$ dollars.
We want to know the total amount of interest paid at the end of the third year.
Total interest $= 3 \times 5000 = 15000$ dollars.
So you can see that by understanding the terminology of “per,” we can use the given data to calculate the future values as well.
Frequently Asked Question
What Does Per Mean In Percentage?
The word per in percentage means the ratio of any number with respect to 100. For example, the percentage of $50$ is basically the ratio of $50$ over $100$. Similarly, the percentage of 10 means $\dfrac{10}{100}$.
Percentages have no dimension. Just like the case with per as it is used to compare two quantities, in the case of percentage, we compare one number with respect to 100, or we take the ratio of one number with respect to 100, and it is dimensionless.
The decimal numbers can also be written or represented as percentages. For example, $0.7 \%$ means $\dfrac{0.7}{100}$. Student marks are expressed in percentage most of the time, and the formula for the percentage can be written as:
Percentage $= \dfrac{actual value}{Total Value} \times 100$
Conclusion
After studying this guide, you now know exactly what is meant by the term “per” and what it is used for. Now you will have a better understanding of the terminologies like $137$ KM per hour, $50$ KW per hour etc. Let us review the major points that we have discussed in this article.
• The word per means “for every,” and it is used to compare one quantity with respect to the other.
• The word per can be referred to as the ratio of two quantities, but we are not actually dividing two quantities to get a number, we are basically comparing the quantities and can use a given ratio as a reference for future calculation.
• The concept of per is vastly used, and it is not only limited to mathematics; it is used in physics, chemistry and applied sciences as well.
Now that you have comprehended the meaning and significance of the word “per”, you can now try to solve different numerical and word problems involving the word “per” and feel more confident about yourself.
