Which Equation is the Inverse of y=9x²-4 – Exploring the Inverse

The captivating allure of mathematics lies in exploring the inverse equation of y = 9x² – 4. By unraveling the inverse of a function, mathematicians can unlock a hidden world where the roles of input and output are reversed, unveiling new insights and possibilities.

Among the myriad functions that have captured the attention of mathematicians, the inverse of y=9x² – 4 stands as a captivating puzzle.

In this article, we embark on a journey into the depths of this inverse, delving into the intricate processes of reflection, transformation, and mathematical reversals. Join us as we traverse the fascinating terrain of the inverse of y=9x² – 4, where mathematical mysteries await unraveling.

Defining the Inverse Equation of y = 9x² – 4

The inverse of a function is a mathematical operation that undoes the original function, effectively swapping the roles of the input and output variables. In the case of the inverse of y = 9x² – 4, we aim to find a new function that, when applied to the output values of the original function, yields the corresponding input values. In other words, we seek a function that, when applied to y, will give us the corresponding x values that satisfy the equation. Below, we present the graphical representation of the function y = 9x² – 4 in Figure-1.

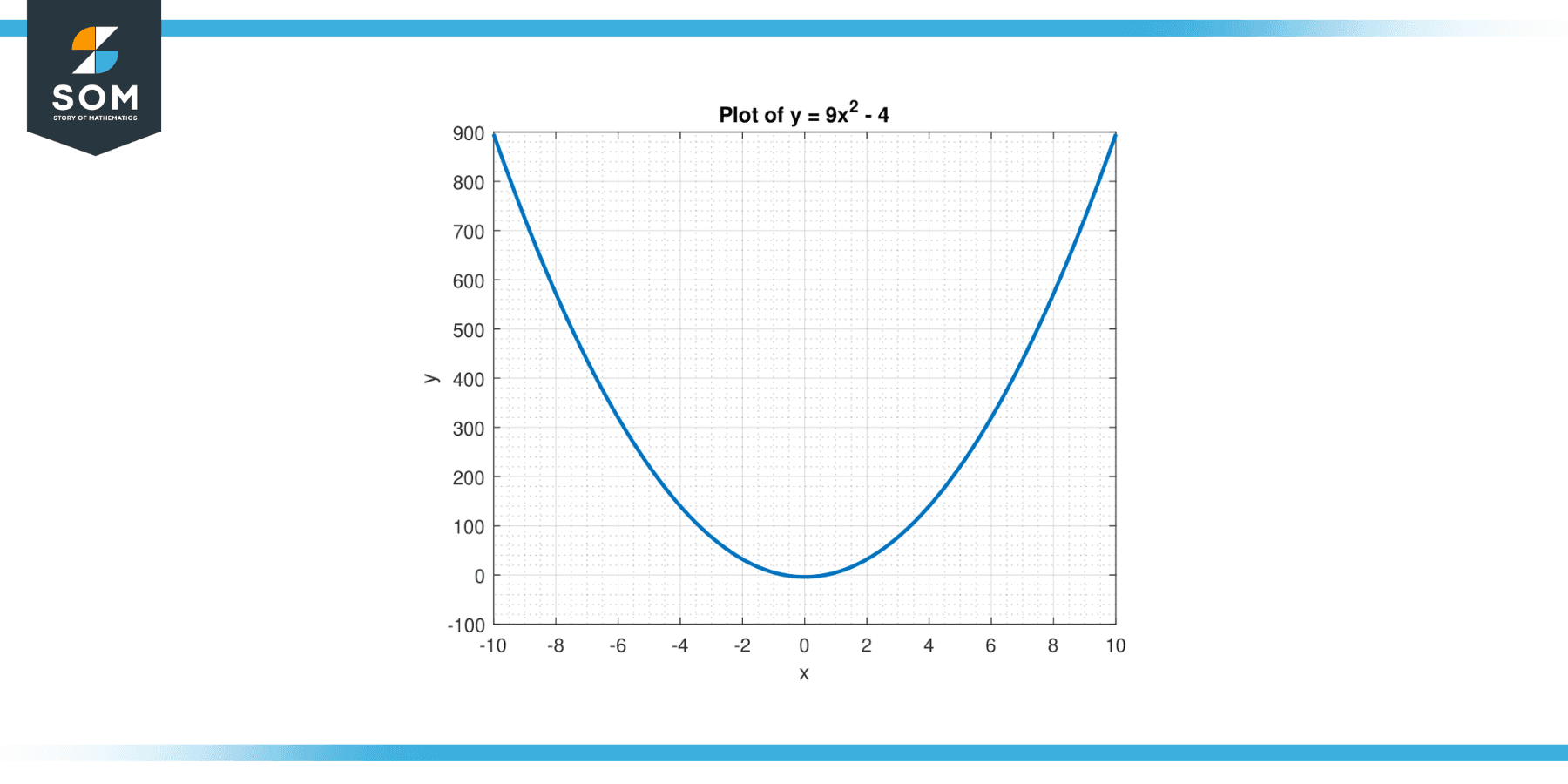
Figure-1.

Mathematically, the inverse of y = 9x² – 4 is denoted as x = (√(y+4))/3 or x = – (√(y+4))/3. The inverse function enables us to explore the relationship between the output and input variables from a different perspective. It provides a powerful tool for solving equations and analyzing the behavior of the original function.

Finding the Inverse of y = 9x² – 4

To find the inverse of the function y = 9x² – 4, we follow these steps:

Step 1

Replace y with x and x with y: Swap the variables x and y in the original equation, giving us the equation x = 9y² – 4.

Step 2

Solve the equation for y: Rearrange the equation to isolate y. In this case, we have:

x = 9y² – 4

x + 4 = 9y²

(1/9)(x + 4) = y²

√((1/9)(x + 4)) = y

Step 3

Consider the positive and negative square root: The equation above has two solutions, taking the positive and negative square root. Therefore, the inverse function has two branches: y₁ = √((1/9)(x + 4))

y₂ = -√((1/9)(x + 4))

Step 4

Write the inverse function: Combine the branches to express the inverse function in a general form. The inverse of y = 9x² – 4 is given by:

f⁻¹(x) = √((1/9)(x + 4))

and:

f⁻¹(x) = -√((1/9)(x + 4))

The inverse function allows us to find the original input values (x) corresponding to given output values (y). By applying the inverse function to a given y, we can determine the corresponding x values that satisfy the equation. Below, we present the graphical representation of the inverse of the function y = 9x² – 4 in Figure-2.

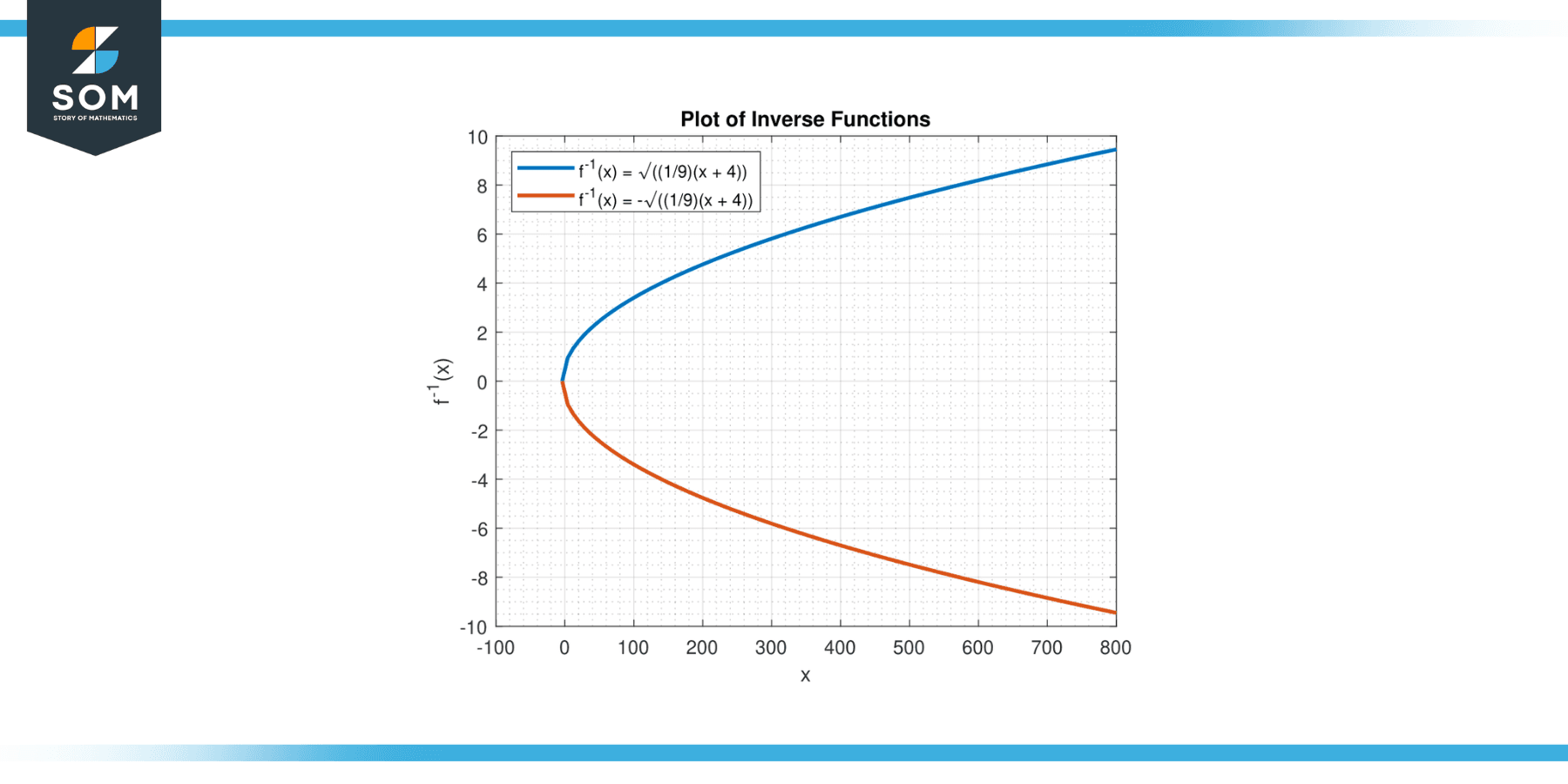
Figure-2.

Applications

The inverse of the function y = 9x² – 4 has various applications across different fields of mathematics and beyond. Here are some notable examples:

Function Reversal and Solving Equations

The inverse function enables us to reverse the roles of input and output variables. In this case, the inverse function allows us to solve equations involving the original function. By finding the inverse of y = 9x² – 4, we can determine the input values (x) corresponding to specific output values (y). This is particularly useful in solving equations where the dependent variable is given, and we need to find the corresponding independent variable.

Curve Sketching and Transformation

The inverse function helps analyze the shape and behavior of the original function. By examining the graph of the inverse function, we can understand the symmetry and transformation properties of the original function y = 9x² – 4. In particular, the inverse function may reveal insights into the original function’s concavity, intercepts, turning points, and other characteristics.

Optimization and Critical Points

In optimization problems, the inverse function can aid in identifying critical points. By analyzing the inverse function, we can determine the input values (x) that yield extreme output values (y). This can be valuable in various applications, such as finding a quantity’s maximum or minimum values.

Data Analysis and Modeling

The inverse function can be employed in data analysis and modeling to understand the relationship between variables. By finding the inverse of a mathematical model, we can obtain an explicit formula for the dependent variable as a function of the independent variable. This allows for better interpretation of the data and facilitates predictions or estimations based on the model.

Physics and Engineering

The inverse function has practical applications in physics and engineering, where mathematical relationships are often encountered. For example, in motion problems, the inverse function can be used to determine the time needed to reach a specific position given the displacement function. In electrical engineering, the inverse function can help solve circuit voltage, current, and resistance problems.

Computer Graphics and Animation

The inverse function finds application in computer graphics and animation, specifically in transformations and deformations. By using the inverse function, designers and animators can manipulate objects and characters to achieve desired effects, such as scaling, rotation, or morphing.

Exercise 

Example 1

Find the inverse function of y = 9x² – 4 and determine its domain and range.

Solution

To find the inverse function, we follow the steps mentioned earlier. First, we swap x and y:

x = 9y² – 4

Next, we solve for y:

x + 4 = 9y²

(1/9)(x + 4) = y

So, the inverse function is: f⁻¹(x) = (1/9)(x + 4)

The domain of the inverse function is the set of all real numbers since there are no restrictions on x. The range of the inverse function is also the set of all real numbers, as every real number can be obtained by substituting values into the inverse function.

Example 2

Find the inverse function of y = 3x² + 2

Solution

To find the inverse function of y = 3x² + 2, we can follow the steps outlined earlier:

Step 1: Swap x and y:

x = 3y² + 2

Step 2: Solve for y:

Rearrange the equation to isolate y. In this case, we have:

3y² = x – 2

y² = (x – 2) / 3

y = ±√((x – 2) / 3)

Step 3: Combine the branches: Since we have a square root, we must consider both the positive and negative branches. Therefore, the inverse function has two branches:

f⁻¹(x) = √((x – 2) / 3)

and:

f⁻¹(x) = -√((x – 2) / 3)

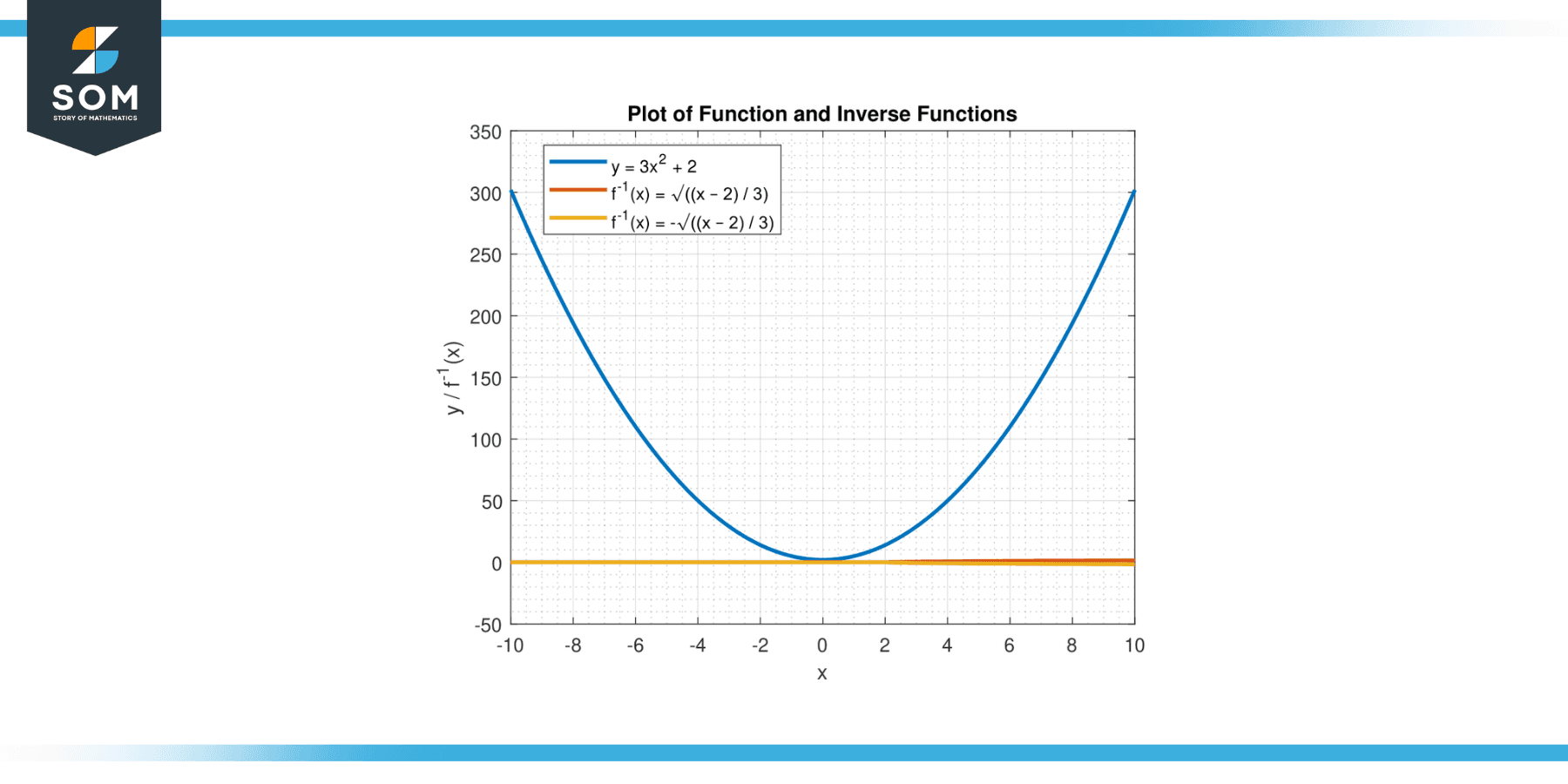
Figure-3.

Example 3

Find the inverse function of y = 2x² + 4x – 1

Solution

To find the inverse function of y = 2x² + 4x – 1, we can follow the same steps as before:

Step 1: Swap x and y:

x = 2y² + 4y – 1

Step 2: Solve for y: Rearrange the equation to isolate y. In this case, we have a quadratic equation:

2y² + 4y – 1 = x

To solve this quadratic equation for y, we can use the quadratic formula:

y = (-b ± √(b² – 4ac)) / (2a)

In this case, a = 2, b = 4, and c = -1. Substituting these values into the quadratic formula, we get:

y = (-4 ± √(4² – 4(2)(-1))) / (2(2))

y = (-4 ± √(16 + 8)) / 4

y = (-4 ± √24) / 4

y = (-4 ± 2√6) / 4

y = -1 ± (√6) / 2

So, the inverse function has two branches:

f⁻¹(x) = (-1 + √6) / 2

and:

f⁻¹(x) = (-1 – √6) / 2

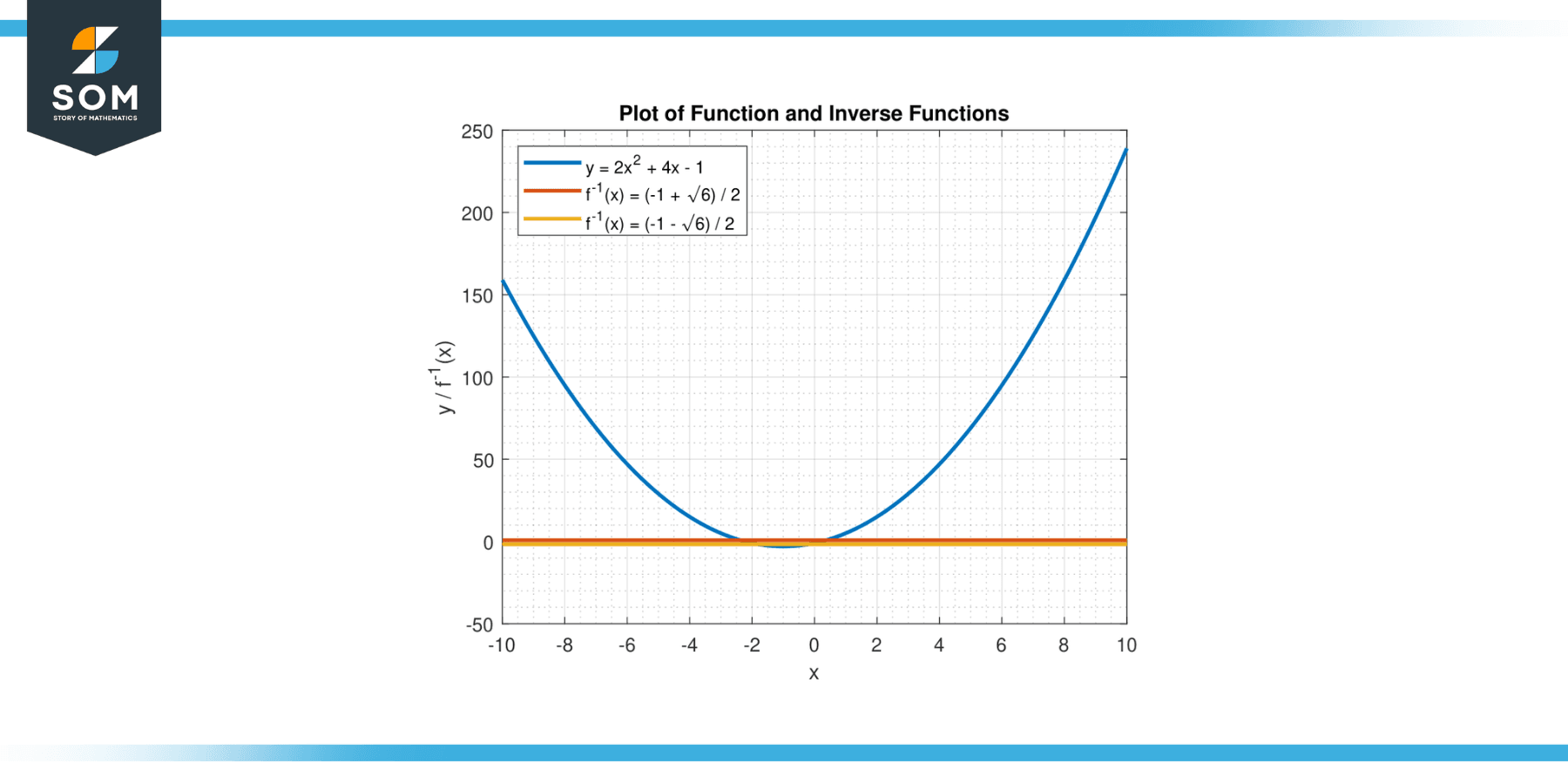
Figure-4.

All images were created with MATLAB.