JUMP TO TOPIC
Dividing 1/infinity does not exist because infinity is not a real number. However, we can find a way to target this problem that is valid and acceptable. Read this complete guide to find out the solution to this problem.
How To Solve 1/Infinity?
Solving $1/\infty$ is the same as solving for the limit of $1/x$ as $x$ approaches infinity, so using the definition of limit, 1 divided by infinity is equal to $0$. Now, we want to know the answer when we divide 1 by infinity, denoted as $1/\infty$, which we know does not exist since there exists no number that is largest among all. However, if we will use the definition of a limit of a function and evaluate the function $1/x$, where $x$ becomes larger and larger, we will see that the function $1/x$ approaches a particular number.
The following table, Table 1, shows the value of $1/x$ as $x$ gets larger and larger.
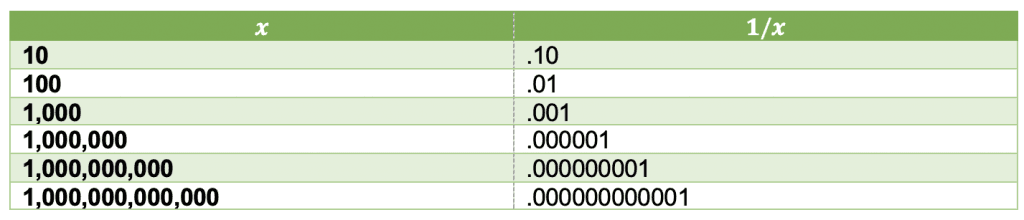
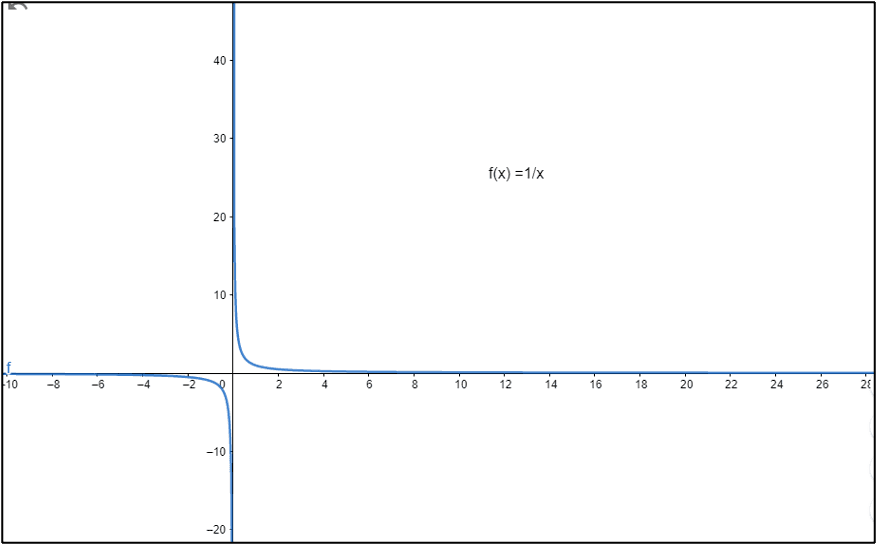
We can see from the graph of $1/x$ that as $x$ approaches infinity, $f(x)=1/x$ approaches $0$. Therefore, solving $1/\infty$ is the same as solving for the limit of $1/x$ as $x$ approaches infinity. Thus, using the definition of limit, 1 divided by infinity is equal to $0$.
Henceforth, we will consider infinity not as a real number where usual mathematical operations can be normally performed. Instead, when we are working with ∞, we make use of this as a representation of a number that increases without bound. Thus, we interpret it as how a certain function will behave when the value of x approaches infinity or increases without bound. We will study some other operations or expressions that work around infinity.
What Is Infinity?
Importance in Mathematics
When we are talking about the largest number, we can notice that we can’t find a specific number or a natural number that is greater than all of the natural numbers.
- $1,000,000$ is a large number, but we can find a larger number than this, which is $1,000,001$.
- $1,000,000,000$ is also a large number, but we can, again, find a number larger than this, which is $1,000,000,001$.
- $10^{100000000000000000}$ is a very large number, still, we can find another larger number than this, we just need to add 1 to it, and we already have one.
So, no matter how big the number that we have, there always exists a bigger number. Since we can never locate the largest real number, we use infinity instead to represent these very large numbers. Hence, infinity is not a real number since we will never find the largest real number.
Dividing by Infinity
We already know that $1/\infty$ is zero Now, for the case of $2/\infty$, $0/\infty$, $-10/\infty$, or $\infty/\infty$, will we still get zero? When the numerator is greater than 1 or less than 1, will the expression be still equal to zero? For the first three expressions, the answer is yes. However, the last expression, $\infty/\infty$, has a different answer, which we will tackle later.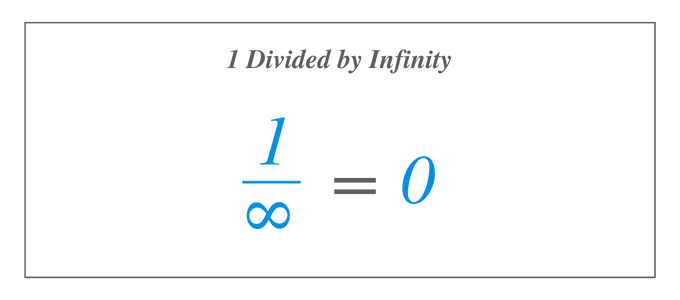
Now, let’s try to solve $2/\infty$. Note that we can express this as the limit of $2/x$ as $x$ approaches infinity. So we have:
\begin{align*}
\dfrac{2}{\infty}&=\lim_{x\to\infty}\dfrac{2}{x}\\
&=\lim_{x\to\infty}\dfrac{2\cdot1}{x}\\
&=2\cdot\lim_{x\to\infty}\dfrac{1}{x}.
\end{align*}
We use the earlier information we gathered that $\lim_{x\to\infty}\dfrac{1}{x}$ is equal to zero. Thus, we have:
\begin{align*}
\dfrac{2}{\infty}=2\cdot0=0.
\end{align*}
Therefore, $2/\infty$ is also zero.
Similarly, since:
\begin{align*}
\dfrac{0}{\infty}&=0\cdot\left(\dfrac{1}{\infty}\right)\\
-\dfrac{10}{\infty}&=-10\cdot\left(\dfrac{1}{\infty}\right),
\end{align*}
then we get that both $0/\infty$ and $-10/\infty$ are equal also to zero. In general, for any real number $c$,
\begin{align*}
\dfrac{c}{\infty}=0.
\end{align*}
Take note that in this generalization, we mentioned that $c$ should be a real number so that $c/\infty$ is zero. Thus, since infinity is not a real number, then $\infty/\infty$ is not equal to zero.
Addition, Subtraction, and Multiplication of Infinities
We can now start to use the term “extremely large number” when referring to infinity so that we can understand better how to perform these operations with infinities.
Note that adding to infinities is like adding to very extremely large numbers. So what happens when we add two extremely large numbers? We still get an extremely large number. Thus,
\begin{align*}
\infty +\infty =\infty.
\end{align*}
Moreover, multiplying two infinities can similarly also be put in this way. If we already have a very large number and we take another very large number, and multiply it with the first very large number, then the product will also be a very large number. Thus, in the same way,
\begin{align*}
\infty \times\infty =\infty
\end{align*}
Now, looking at the difference between two infinities, we have two very extremely large numbers. Since these very large numbers are undefined or just a representation of a very large number, then we will never know if the two very large numbers are equal or if one of the very large numbers exceeds the other. Thus, infinity minus infinity is undefined.
\begin{align*}
\infty – \infty = \text{undefined}
\end{align*}
What Is Infinity Divided by Infinity?
Infinity divided by infinity is undefined, meaning it is not equal to any real number. Since infinity divided by infinity is definitely not equal to zero, we can answer right away that it is equal to 1 because the numerator and denominator are the same. In fundamental operations, we know that any number, except 0, when divided by itself, equals one. That is, whenever a is a nonzero real number, we have:
\begin{align*}
\dfrac{a}{a}=1.
\end{align*}
However, this rule does not apply in the case of $\infty/\infty$ because infinity is not a real number. So we find another way to show that infinity divided by infinity is indeed undefined. We use the information we obtained in the previous section.
We assume that $\infty/\infty=1$. Then, we use the fact that $\infty+\infty=\infty$. So, we have:
\begin{align*}
\dfrac{\infty}{\infty}&=\dfrac{\left(\infty+\infty\right)}{\infty}\\
&=\dfrac{\infty}{\infty}+\dfrac{\infty}{\infty}\\
\end{align*}
Since $\infty/\infty=1$, then this should be true:
\begin{align*}
\dfrac{\infty}{\infty}&=\dfrac{\infty}{\infty}+\dfrac{\infty}{\infty}\\
1&=1+1\\
1&=2.
\end{align*}
This is a contradiction because 1 will never be equal to 2. Thus,$\infty/\infty$ is undefined.
Infinity Divided by a Real Number
In the case where the numerator is infinity and the denominator is a real number, say $c$, then
\begin{align*}
\dfrac{\infty}{c}=\infty.
\end{align*}
Note that this only holds for nonzero real numbers. Consider a very large number divided into finite parts. Then, each part or share is still a large number since the initial number is extremely large.
What is 1/infinity^2?
The expression $1/\infty^2$ is equal to zero. This is because
\begin{align*}
\dfrac{1}{\infty^2}&=\dfrac{1}{\left(\infty\times\infty\right)}\\
&=\dfrac{1}{\infty}\\
&=0.
\end{align*}
Is 1^Infinity = e?
The answer to this question is not always. The expression $1^{\infty}$ is considered one of the indeterminate forms, meaning that it will have different answers depending on which situation it was used. Take note that expressions with infinity can be taken as an expression to represent a limit of a certain function where $x$ approaches infinity.
Thus, in the case of limits that will give a $1^{\infty}$, different methods can be used to move forward from this indeterminate form and derive a limit for the function as $x$ increases without bound.
Evaluate e^Infinity
Conclusion
Infinity is a mathematical term, concept, or symbol that is oftentimes carelessly utilized in mathematical solutions, especially in limit-finding problems. Let’s recall the important notes we learned in this discussion.
- Infinity is not a real number and is only used as a representation for an extremely large real number.
- Dividing 1 by infinity is equal to zero.
- In general, any real number divided by infinity is zero, and the quotient of nonzero real numbers that divide infinity is infinity.
- The sum and product of two infinities are equal to infinity, while the difference and quotient of two infinities are undefined.
- $1^{\infty}$ is an indeterminate form.
In this article, we defined infinity in a clearer manner and used it to perform operations and evaluate expressions with infinities.