Evaluate 512/2

Solving 512/2

Evaluate 512/2Evaluating 512/2 is equal to 256. How did we arrive at that answer? We simply solve for the quotient when 512 is divided by 2. We can hit our calculators and plug in 512/2 to get the answer, but if calculators are not allowed, we need to perform integer divisions to arrive at our answers.

To check the quotient when we divide 512 by 2, we first need to get the absolute values of 512 and 2, which are the following:

\begin{align*}
|512|=512
\end{align*}
since it is greater than 0, and
\begin{align*}
|2|=2
\end{align*}
since it is also greater than 0.

Since we now have the absolute values of the two integers, we will now divide it normally, as follows:

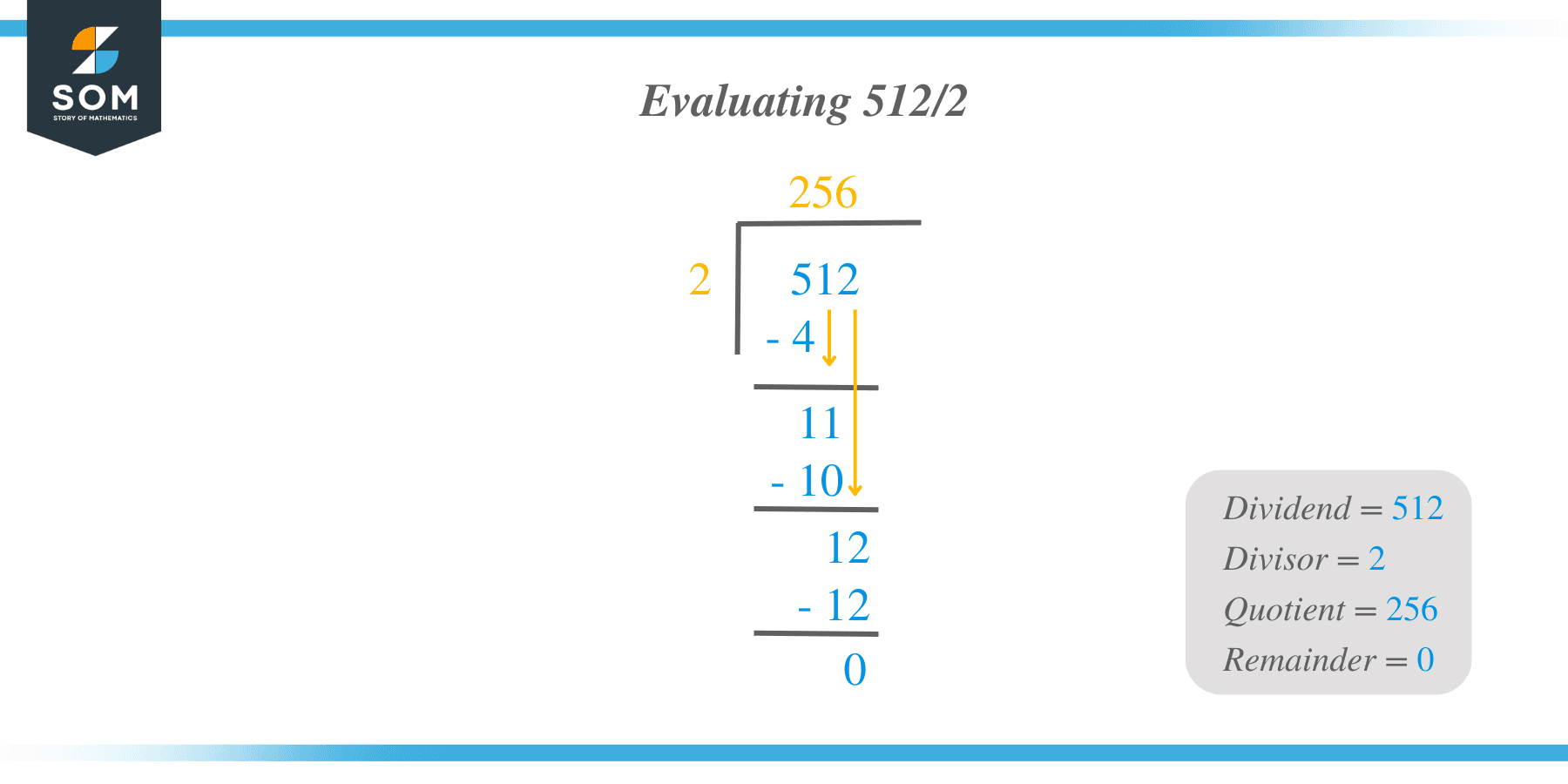
Evaluate 512 div 2
Evaluate 512 div 2

For the last step, let’s examine the signs of 512 and 2. Since they are both positive, then the quotient is also positive. Thus, $\dfrac{512}{2} = 256$.

What Is Integer Division?

Integer division is a division operation between two integers. Suppose we want to know the quotient when $a$ is divided by $b$, where $a$ and $b$ are integers, then we need to evaluate $\dfrac{a}{b}$. We call $a$ the dividend, and $b$ as the divisor. Take note that $\dfrac{a}{b}$ is different from $\dfrac{b}{a}$.

Steps in Integer Division

Let $a$ and $b$ be two integers and we need to solve for $\dfrac{a}{b}$.

Step 1

 First, we need to get the absolute of $a$ and $b$, denoted as $|a|$ and $|b|$, respectively.

The absolute value of a number $x$ is defined as:
\begin{align*}
|x|&=x \,\text{whenever}\, x≥0, \text{and}\\
|x|&=-x \,\text{whenever}\, x<0.
\end{align*}

Step 2

Since both of the integers are already nonnegative, we will divide normally $|a|$ by $|b|$.
 

Step 3

In the final step, we need to look at the signs of $a$ and $b$. Let us say that the quotient of $\dfrac{|a|}{|b|}$ is $x$. If these two numbers are both positive or both negative, then the quotient sign will be positive. Hence, $\dfrac{a}{b}=x$.

However, if these two integers have different signs, meaning one number is positive and the other one is negative, then the quotient sign will be negative. So we will need to put a negative sign in the quotient of $|a|$ divided by $|b|$. Hence, $\dfrac{a}{b}=-x$.

Some Notes and Restrictions

Take note that the divisor should not be equal to zero. The quotient is undefined whenever the divisor is zero because we cannot divide any number by zero.
\begin[align*}
a/0=undefined
\end{align*}

However, we can always divide zero by any nonzero integer and the quotient will always be zero.
\begin{align*}
0/b=0
\end{align*}

Evaluating 256/2

Note that 256 and 2 are both positive integers, so we can skip the first step and proceed with getting the quotient. It is also guaranteed that the quotient is positive since the dividend and divisor are both positive.
We can express 256 as:
\begin{align*}
256=200+50+6.
\end{align*}

So that:
\begin{align*}
\dfrac{256}{2}&=\dfrac{\left(200+50+6\right)}{2}\\
&=\dfrac{200}{2}+\dfrac{50}{2}+\dfrac{6}{2}\\
&=100+25+3\\
&=128
\end{align*}

Therefore:
\begin{align*}
\dfrac{256}{2}=128.
\end{align*}

Solve for 512/3

Evaluating $\dfrac{512}{3}$ is the same as how we obtain the quotient of $\dfrac{512}{2}$. We can also skip the first step since 512 and 3 are both positive integers. Thus, their absolute values are still themselves.

Similarly, we can use the normal division to get the quotient, or we can use the technique we used in the previous example. We can express 512 as:
\begin{align*}
512=500+10+2
\end{align*}

Thus, dividing 512 by 3, we have:
\begin{align*}
\dfrac{512}{3} &=\dfrac{\left(500+10+2\right)}{3}\\
&=\dfrac{\left(300+200+10+2\right)}{3}\\
&=\dfrac{300}{3}+\dfrac{\left(210+2\right)}{3}\\
&=\dfrac{300}{3}+\dfrac{210}{3}+\dfrac{2}{3}\\
&=100+70+\dfrac{2}{3}\\
&=170 \dfrac{2}{3}.
\end{align*}

Therefore, $\dfrac{512}{3}$ is equal to $170 \dfrac{2}{3}$. However, note that 512 is not divisible by 3 because the quotient is not an integer. This means that we have a remainder of 2 when we divide 512 by 3.

Solving 512/4

From the previous example, we get that 512 is not divisible by 3. Here, let’s check whether 512 is divisible by 4, which means that the quotient of $\dfrac{512}{4 }$ has no remainder or an integer.We rewrite 512 in the same manner as the previous example. \begin{align*} 512=500+10+2 \end{align*}Then, we divide both sides by 4. So we have: \begin{align*} \dfrac{512}{4} &=\dfrac{\left(500+10+2\right)}{4}\\ &=\dfrac{\left(400+100+10+2\right)}{4}\\ &=\dfrac{\left(400+\left(80+20\right)+10+2\right)}{4}\\ &=\dfrac{\left(400+80+32\right)}{4}\\ &=\dfrac{400}{4}+\dfrac{80}{4}+\dfrac{32}{4}\\ &=100+20+8\\ &=128. \end{align*}Hence, evaluating $\dfrac{512}{4}$, we get the quotient 128.

Evaluating 512/22

We now try to find the quotient where the divisor is bigger or not a one-digit integer. In evaluating $\dfrac{512}{22}$, we try which technique or expression of 512 will make it easier to solve.

We rewrite 512 so that we have addends that are divisible by 22:
\begin{align*}
512&=500+10+2\\
&=\left(440+60\right)+10+2\\
&=440+70+2\\
&=440+\left(66+4\right)+2\\
&=440+66+6
\end{align*}

Now, dividing both sides by 22, we have:
\begin{align*}
\dfrac{512}{22}&=\dfrac{\left(440+66+6\right)}{22}\\
&=\dfrac{440}{22}+\dfrac{66}{22}+\dfrac{6}{22}\\
&=20+3+\dfrac{6}{22}\\
&=23 \dfrac{6}{22}.
\end{align*}

Hence, we get that $\dfrac{512}{22}$ is equal to $23 \dfrac{6}{22}$. Similar with solving for $\dfrac{512}{3}$, we get that 512 is not divisible by 22 since the quotient that we obtained is not an integer. Moreover, we get a remainder of 6 when 512 is divided by 22.

Simplify 512^2/3

We try to simplify the expression $\dfrac{512^2}{3}$ using the quotients we already obtained from the previous examples.

Note that $512^2=512\times512$. So we can write $\dfrac{512^2}{3}$ as:
\begin{align*}
\dfrac{512^2}{3}&=\dfrac{\left(512×512\right)}{3}\\
&=\dfrac{512\times512}{3}.
\end{align*}

We get from the previous example that $\dfrac{512}{3}=170 \dfrac{2}{3}$. Thus, we have:
\begin{align*}
\dfrac{512^2}{3}&=512\times\left(170 \dfrac{2}{3}\right)\\
&=\left(512\times170\right)+\left(\dfrac{\left(2\times512\right)}{3}\right)\\
&=\left(512\times170\right)+\left(2×170 \dfrac{2}{3}\right)\\
&=\left(512\times170\right)+\left(340 \dfrac{4}{3}\right)\\
&=\left(512\times170\right)+\left(341 \dfrac{1}{3}\right)\\
&=87,040+341 \dfrac{1}{3}\\
&=87,381 \dfrac{1}{3}.
\end{align*}

Thus, without expanding the value of $512^2$, we are able to simplify $\dfrac{512^2}{3}$ and derive the quotient $87,381 \dfrac{1}{3}$.

Why Do We Need To Learn To Solve 512/2?

It is important to learn how to divide integers because it allows us to get a simplified version of the expression we are trying to divide. We obtain the exact quotients and values of the expression expressed as a ratio of two integers. Solving 512/2 also lets us know that 512 is divisible by 2 because we get a quotient that is also an integer. Thus, integer division is a good test to check the divisibility of integers or find divisors of an integer.

FAQ

What Is 512^(2/3) Radical Notation?

When we express $512^\left(2/3\right)$ in radical notation, we have $\sqrt[3]{\left(512\right)^2}$ or $\left(\sqrt[3]{512}\right)^2$. The denominator of the exponent indicates the degree of the roots of the radical, while the numerator of the exponent is the power inside the radical sign or outside the whole radical sign. Either way, you will have the same value when the expression is simplified further or evaluated.

Solve 512=2^n?

The answer to this is $n=9$ since $512=2^9$. Given $512=2^n$, we solve for $n$. That is, we need to express 512 as a power of 2. We list down the powers of 2:
\begin{align*}
2^0&=1\\
2^1&=2\\
2^2&=4\\
2^3&=8\\
2^4&=16\\
2^5&=32\\
2^6&=64\\
2^7&=128\\
2^8&=256\\
2^9&=512
\end{align*}

Thus, we obtain that $n=9$ since $512=2^9$.

Simplify 512^(2/3)?

Simplifying $512^{\left(2/3\right)}$ we get that the expression is equal to 64. Here is how we get that.Note that from the previous question, we know that $512=2^9$. Thus, we have: \begin{align*} 512^{\left(2/3\right)}&=\left(2^9\right)^{\left(2/3\right)}\\ &=2^{\left(9\times2\right)/3}\\ &=2^6\\ &=64. \end{align*}Hence, we verified that $512^{\left(2/3\right)}=64$.

What Is the Value of 512^-2/9?

The value of $512^{\left(-2/9\right)}$ is $\dfrac{1}{4}$. We use the information and technique we obtained in the previous examples to verify our answer. Note that since the exponent is negative, then we get the reciprocal of $512^{\left(2/9\right)}$. So we have:
\begin{align*}
512^{\left(-2/9\right)}&=\dfrac{1}{512^{\left(2/9\right)}}\\
&=\dfrac{1}{\left(2^9\right)^{\left(2/9\right)}}\\
&=\dfrac{1}{2^2}\\
&=\dfrac{1}{4}.
\end{align*}

Therefore, the value of $512^{\left(-2/9\right)}$ is equal to $\dfrac{1}{4}$.

Conclusion

Of all the four operations, addition, subtraction, multiplication, and division, we know that division is considered the hardest among them. Let us now summarize the points we learned.

  • Solving for 512/2 involves integer division that will give us a quotient of 256.
  • Integer division is performed when you are solving the quotient of two integers.
  • In integer division, we take note of the signs of the integers to also determine the sign of the quotient.
  • We also learned that 512 is divisible by 2 and 4 but not divisible by 3 and 22.
  • Evaluating the quotient of two integers is important because it allows us to test the divisibility of an integer to other integers.

In this article, we defined the process of performing integer division. We also provided examples and reasons why it is important to learn how to solve these problems.