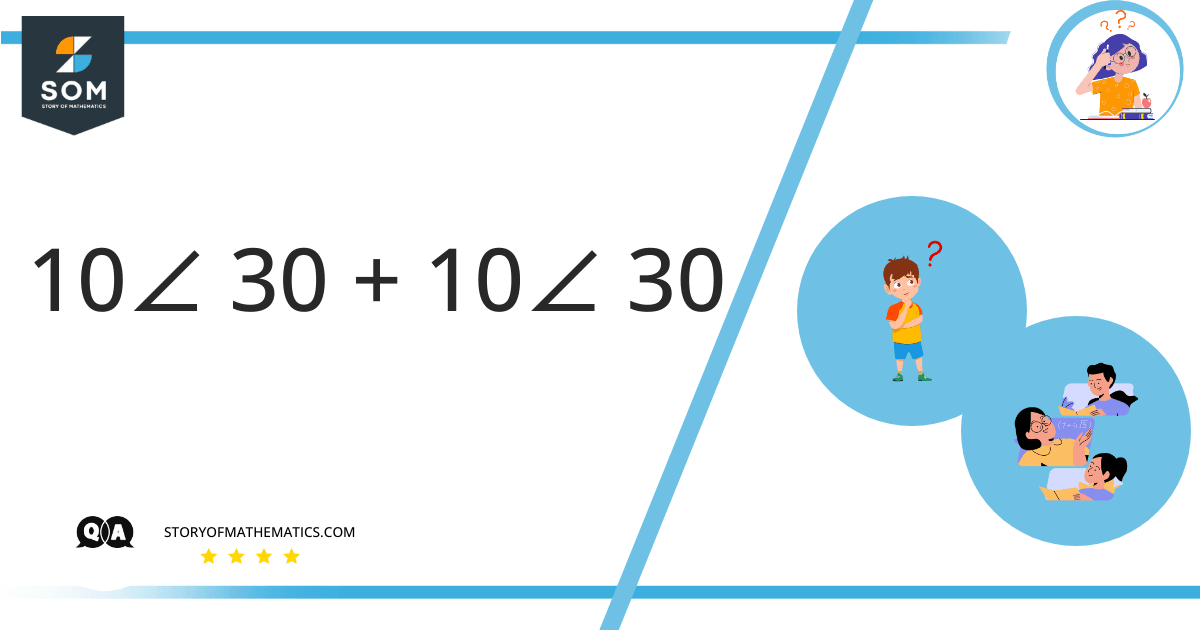
This question aims to split the given polar form into cartesian coordinate form.
This question uses the concept of splitting the given polar form into its cartesian coordinate form. Cartesian coordinate form is the sum of the squared values of the difference between the x coordinate and the y coordinate of the two specified points and is used to calculate the distance between them.
Expert Answer
We are given:
\[10 < 30 + 10 < 30 \]
We know that any polar form can be split into its cartesian coordinate form.
\[r \space < \space \theta \space = \space\begin{bmatrix} r cos \theta\\ r sin \theta \end{bmatrix}\]
We know that:
\[r \space = \space 10\] and \[\theta \space =30\]
By putting values, we get:
\[10\space < \space 3 0 \space = \space\begin{bmatrix} 1 0 cos 3 0\\ 1 0 sin 3 0 \end{bmatrix}\]
Now:
cos ( 3 0) is equal to $\frac{\sqrt 3}{ 2 } $ and sin (3 0 ) is equal to $ \frac{1}{2} $.
By putting values, we get:
\[10\space < \space 3 0 \space = \space\begin{bmatrix} 1 0 \frac{\sqrt 3}{ 2 }\\ 1 0 \frac{1}{2} \end{bmatrix}\]
Simplifying it results in:
\[10\space < \space 3 0 \space = \space\begin{bmatrix} 5 \sqrt 3\\ 5 \end{bmatrix}\]
Consequently, another polar coordinate is exactly the same. We’ll just summarize them now:
\[10 < 30 \space + \space 1 0 < 3 0 \]
\[\begin{bmatrix} 5 \sqrt 3\\ 5 \end{bmatrix} \space + \begin{bmatrix} 5 \sqrt 3\\ 5 \end{bmatrix}\]
\[ \begin{bmatrix} 10 \sqrt 3\\ 10 \end{bmatrix}\]
Now:
$ r $ = $ 20 $ and angle which is $ \theta $ is $30 $.
The final answer is:
\[r \space < \space \theta \space = \space 20 < 30 \]
Numerical Answer
The cartesian coordinate for the given expression is:
\[r \space < \space \theta \space = \space 20 < 30 \]
Example
Represent the given expression $ 20 < 30 + 20 < 30 $ in its cartesian coordinate form.
We are given:
\[20 < 30 + 20 < 30 \]
We know that any polar form can be split into its cartesian coordinate form.
\[r \space < \space \theta \space = \space\begin{bmatrix} r cos \theta\\ r sin \theta \end{bmatrix}\]
We know that:
\[r \space = \space 20\] and \[\theta \space =30\]
By putting values, we get:
\[20\space < \space 3 0 \space = \space\begin{bmatrix} 2 0 cos 3 0\\ 2 0 sin 3 0 \end{bmatrix}\]
Now:
cos ( 3 0) is equal to $\frac{\sqrt 3}{ 2 } $ and sin (3 0 ) is equal to $ \frac{1}{2} $.
By putting values, we get:
\[20\space < \space 3 0 \space = \space\begin{bmatrix} 2 0 \frac{\sqrt 3}{ 2 }\\ 2 0 \frac{1}{2} \end{bmatrix}\]
Simplifying it results in:
\[10\space < \space 3 0 \space = \space\begin{bmatrix} 10 \sqrt 3\\ 10 \end{bmatrix}\]
Consequently, another polar coordinate is exactly the same. We’ll just summarize them now:
\[20 < 30 \space + \space 2 0 < 3 0 \]
\[\begin{bmatrix} 10 \sqrt 3\\ 10 \end{bmatrix} \space + \begin{bmatrix} 10 \sqrt 3\\ 10 \end{bmatrix}\]
\[ \begin{bmatrix} 10 \sqrt 3\\ 10 \end{bmatrix}\]
Now:
r = 40 and angle which is $ \theta $ is 30.
The final answer is:
\[r \space < \space \theta \space = \space 40 < 30 \]
