JUMP TO TOPIC
 A 270 degree angle is three-fourths or $\dfrac{3}{4}$ of the complete circular angle of $360^{o}$.
A 270 degree angle is three-fourths or $\dfrac{3}{4}$ of the complete circular angle of $360^{o}$.
Angles are formed by the intersection of two lines or rays, and the space between the intersection of lines or rays is called the angle. The angle of 270 degrees is greater than a right angle, an example of a reflex angle.
This guide will help you understand the concept of an angle. What is meant by $270$ degrees angle, and how you can draw a $270$ degree-angle using geometrical tools?
What Is a 270 Degrees Angle?
The angle of $270$ degrees is an angle that is three times a right angle, i.e., $3 \times 90^{o} = 270^{o}$. We can also write the $270$ degrees angle as $270^{o}$, which is also greater than $180^{o}$ or a straight line. The $270$ degrees angle is an example of a reflexive angle because any angle greater than $180^{o}$ is called a reflexive angle.
What It Looks Like
We can draw the $270$ degrees angle using a protractor or a compass and other necessary tools. It is pretty easy to draw the $270^{o}$ angle using a protractor, as all we have to do is subtract the internal angle from the total angle of $360^{o}$. Consider the example of a clock. We have $0^{o}$ or $360^{o}$ at $12$. Measuring the angle from $12$ to $9$ will give us $270^{o}$ angle.
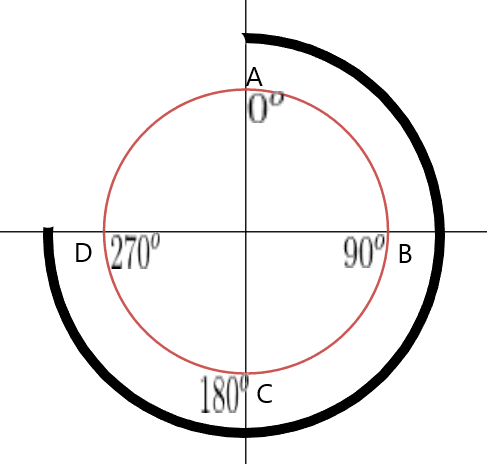
We know the angle of $270$ degrees is reflexive as it is greater than $180^{o}$ but less than $360^{o}$. If we are to draw the 270-degree angle on a unit circle, it will roughly look like the angle given in the figure below.
We start at $0^{o}$ or point A and end up at point D in a clockwise movement to get $3 \times 90^{o}= 270^{o}$.
Drawing a 270 Degrees Angle Using a Protractor
Let us discuss the steps which are involved in drawing an angle of $270$ degrees with the use of a protractor.
Step 1: The first step involves placing the protractor so that the center of the protractor aligns with the $0^{o}$ line. The line at which the protractor is placed is known as the reference line.
Step 2: The second step involves marking the point at $270^{o}$. We know that the reference line makes a $180^{o}$ in an anti-clockwise manner, and if we continue in the same direction and add another $90^{o}$, then it will make an angle of $270^{o}$.
Step 3: In the third step, we join the marked point with the center of the line at $0^{o}$, so the total angle formed is $270$ degrees.
Let’s take an example of angle ABC measuring $270^{o}$. Let us discuss the steps involved in the construction of this angle.
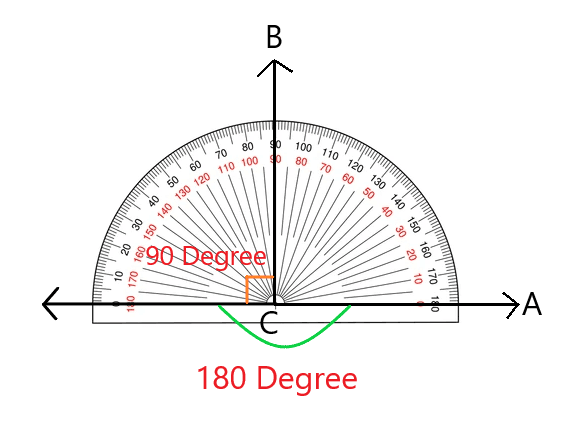
Step 1: Draw two line segments, AC and BC, in an X-Y plane such that the line AC is perpendicular to line BC.
Step 2: Now, place the protractor so that its center aligns with the origin of the lines we draw in the first step. So, the center of the protractor should align with $0^{o}$ of line segments AC and BC.
Step 3: In the third step, mark the point $180^{o}$ in conjunction with the reference line AC.
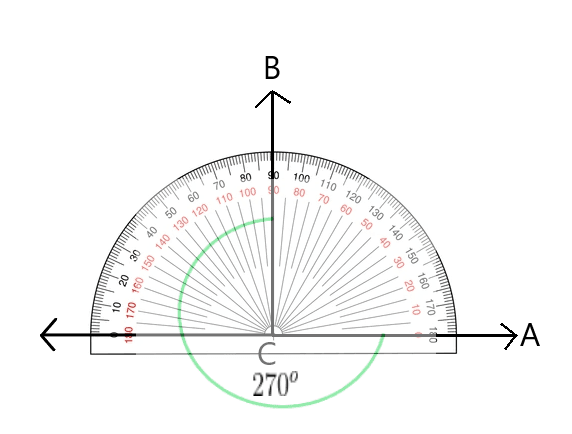
Step 4: In this step, we add an extra $90^{o}$ to the point marked in step 3 as the $180^{o}$ angle.
Step 5: Once we have added the extra $90^{o}$ with the $180^{o}$, we get $180^{o} + 90^{o} = 270^{o}$. Therefore the reflexive angle ABC will be $270^{o}$.
Step 6: In the last step, we can verify the measure of the interior angle ABC whether it is equal to $270^{o}$ or not. We can simply verify it by subtracting $90^{o}$ from the $360^{o}$ and hence verify that interior angle ABC = $360^{o} – 90^{o} = 270^{o}$.
Note: You can exchange the order of steps 5 and step 6 to verify one step with the other step.
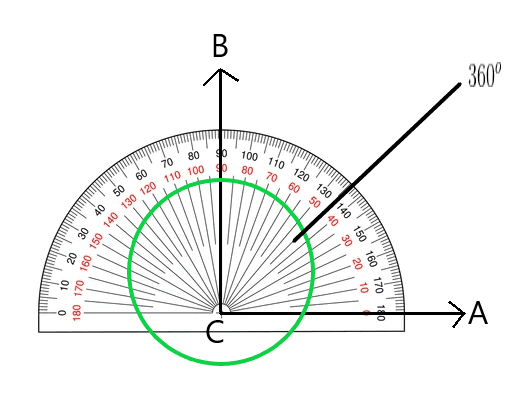
As shown in the figure above, if we remove the 90^{0} made between BC and AC from the circle, we will get 270^{o}.
How To Construct an Angle of $270$ Degrees Without a Protractor
This section will discuss how to construct an angle of $270^{o}$ when a protractor is unavailable. It is essential to learn this technique because this will help you better understand drawing the angles in geometry and will help you solve complex problems.
We have discussed in the previous section that $270^{o} = 360^{o} – 90^{o}$. Therefore, by using the compass and the ruler along with other accessories, we will first draw the 90 degrees angle, then find the reflex of that angle which will be equal to the $270$-degree angle. We give the steps below.
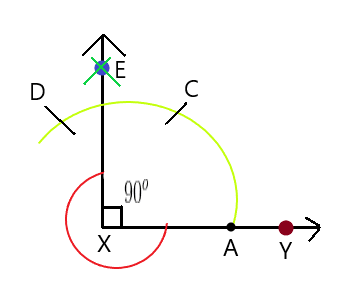
Step 1: Draw a line segment XY using a ruler.
Step 2: In the second step, place the compass at point X or at origin and draw an arc so that it cuts the line segment XY, and the point where it cuts is taken as point A.
Step 3: Now place the compass at point A and the second end at point X. Now keep it steady and draw the arc with a radius to AX then mark the point of intersection as point C.
Step 4: Now place the compass at the intersection point C and draw another arc of the same radius (AX) using a compass and mark the next intersection point as D.
Step 5: Continuing step 4, we keep the compass at point D and draw another arc of radius AX between points C and D.
Step 6: Now, we place the compass at point C and draw another arc intersecting point E.
Step 7: Join the point “E” with point X. This will be a straight perpendicular line which makes an angle of 90^{o}.
Step 8: Finally, you can verify that the reflex angle EXY = $360^{o} – 90^{o}= 270^{o}$. Thus, the reflex angle EXY is the required angle.
How To Convert 270 Degrees Into Radians
So far, we have discussed the angle in degrees, but sometimes we can also give the angle in radians, or you can be asked to convert the angle into radians, so it is essential that you know how to convert 270^{o} into radians or in $\pi$ form.
Let us now convert $270$ degrees into $\pi$. To convert degrees to radians, we basically divide the given angle by $\dfrac{\pi}{180^{o}}$. In this case, we want to convert $270^{o}$ into radians, so $270$ degrees = $270^{o} \times \dfrac{\pi}{180^{o}} $. We know that $1$ degree is equal to $\dfrac{\pi}{180^{o}}$, hence $270$ degree = $270^{o}\times 0.0174$ = $4.712$ radians Thus, the 270-degree angle is equal to $\dfrac{3\pi}{2}$ radians or $4.71239$ radians. The steps to convert 270 degrees in terms of pi or radian are given below.
Step 1: In the first step we put in the desired value of the angle in the formula x (radians) = $x\hspace{1mm} (in degrees) \times \dfrac{\pi}{180}$. Plugging in the 270 degrees in the formula
Radian measurement = $\dfrac{(270^{o} \times \pi)}{180^{o}}$
Step 2: The second step involves re-arranging of the terms.
Radian measurement = $\pi \times \dfrac{270^{o}}{180^{o}}$
Step 3: Now it’s time to solve the equation.
The greatest common divisor for $270$ and $180$ is $90$, so dividing both by $90$, we will get:
$\pi \times \dfrac{3}{2}$ which is equal to $1.5\pi$, so in terms of $\pi $the $270$ degree is equal to $1.5\pi$, and when we convert it to a real number, it will give us the units in radians, and that is
$270^{o} = 4.7123$ radians.
Example 1: Find the value of $3$ times $270^{o}$ in radians.
Solution:
We have already proved that $270$ degrees = $4.7123$ radians, and we want to calculate 3 times the value of $270^{o}$.
Hence, $3 \times 270$ degrees = $3 \times 4.7123$ = $14.1369$ radians.
Thus, the $3$ times value of $270^{o}$ in radians equals $14.1369$.
Example 2: Find the value of $5$ times $270^{o}$ in radians.
Solution:
We have already proved that $270$ degrees = $4.7123$ radians, and we want to calculate 5 times the value of $270^{o}$.
Hence, $5 \times 270$ degrees = $5 \times 4.7123$ = $23.5615$ radians.
Thus, the 5 times value of $270^{o}$ in radians equals $23.5615$.
Example 3: Is $-90^{o}$ equivalent to $270^{o}$?
Solution:
This is a tricky question, and one can get confused while answering it. The answer to the question is yes, $-90^{o}$ equals $270^{o}$.
The angle can be positive or negative. If we subtract $(+90^{o})$ from $360^{o}$, it will give us $270$ degrees. This angle is 270 degrees clockwise angle.
If we move 270 degrees on a circle in a clockwise direction, the $270$ degrees is at 9 o clock, while if we move in an anti-clockwise direction, the same angle will be $-90^{o}$. So, the 270 degrees counterclockwise equals $-90^{o}$ as both will have the same initial and terminal rays.
Practice Questions:
1. What is the value of $6$ times $270$ degrees in terms of radians?
2. Calculate the following
- sin 270 degrees
- cos 270 degrees
- tan(270 degrees)
Answer Keys:
1)
We know that a $270$ degrees = $4.71239$ radians.
Therefore, $6 \times 270$ degrees = $6 \times 4.71239$ radians = $28.27434$ radians.
Thus, the value of $2$ times $270$ degrees in terms of radians is $28.27434$ radians.
2)
- sin($270^{o}$) = $-1$
- cos($270^{o}$) = $0$
- tan($270^{o}$) = undefined
