JUMP TO TOPIC
 The upside down U in math, i.e., “$\cap$” is the symbol of intersection.
The upside down U in math, i.e., “$\cap$” is the symbol of intersection.
Mathematical symbols like “$\cap$” and “$\cup$” are frequently used in set theory. If we invert the normal union symbol “$\cup$,” then we will get an upside-down U symbol “$\cap$”. Union and intersection concepts are heavily used in solving problems related to Sets and Venn diagrams.
In this topic, we will study the upside down U in math, its significance, and the difference between simple U and upside down U along with numerical examples and applications
What Is the Upside Down U in Math?
The upside-down U in math is commonly known as an intersection between two or more sets, which is the collection of common elements of all the sets. For example, if we are given Set A $= { Red, Yellow, Blue}$ and Set B $= { Pink, Yellow, Green}$ then the intersection between these two sets Set A and Set B will be $= {Yellow}$. We can see that yellow was the only color which was present in both the sets, so when we take the intersection between these two sets, yellow is our answer.
Sets
The upside-down “$\cup$” or “$\cap$” is used to solve sets for designing a Venn diagram or solving probability problems. So what is a set and do we use the intersection only for sets? Yes, unions and intersections are primarily used in solving set problems.
A set is a specific collection of well-defined elements or objects and we use the concepts of union and intersection to study the properties of the elements of the set, like what is common in these elements or whether all of them are distinct and what will happen if we combine two or more sets to form a superset. All these properties of the sets like combinations, permutations and other properties are studied by using the concepts of union and intersection.
Intersection of Sets
The intersection sign is denoted by “$\cap$”, so if we have given two sets $X$ and $Y$, then the intersection between these two sets is written as X $\cap$ Y. The formula for the intersection between two sets can be written as:
X $\cap$ Y = {y : y $\in$ X and y $\in$ Y}
So if we are given two sets, X and Y, then “$y$” will be the element for X $\cap$ Y if and only if “$y$” is present in both the sets or in other words “$y$” is the only common element in both the sets and it is also called the intersection formula of the sets.
Suppose we take two sets, A and B, then the intersection between these two sets is represented by the Venn diagram drawn below:
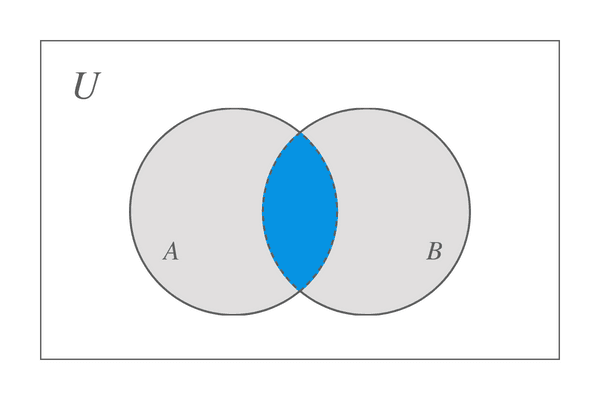
We can conclude that the intersection of set A and B will give us the set that only contains the common elements of set A and B. But what would happen if one of the sets contains nothing? In this scenario, when one of the sets is empty while the other contains some elements, so we don’t have any common elements, the result will also be an empty set. For example, we have set $X$ and $Y$, the set $Y$ = {$\emptyset$} then X $\cap$ Y = {$\emptyset$}.
Difference Between U and Upside Down U
The simple or normal U is the union sign, and when we are taking the union of two sets, then it means the resultant set will include all the elements of both sets with the only condition that the same elements are written once. For example if $A$ = {$1,2,3$} and $B$ = {$2,3,4$} then:
$A \cup B$ = {$1,2,3$} $\cup$ {$2,3,4$} = {$1,2,3,4$}
In the case of upside down U, we just take the intersection between the given sets, i.e. the answer will contain only the common elements between the sets. For example, if $A$ ={$1,2,3$} and $B$ = {$1,2$} then
$A \cap B$ = {$1,2,3$} $\cap$ {$1,2$} = {$1,2$}
Let us now study upside down U in math examples.
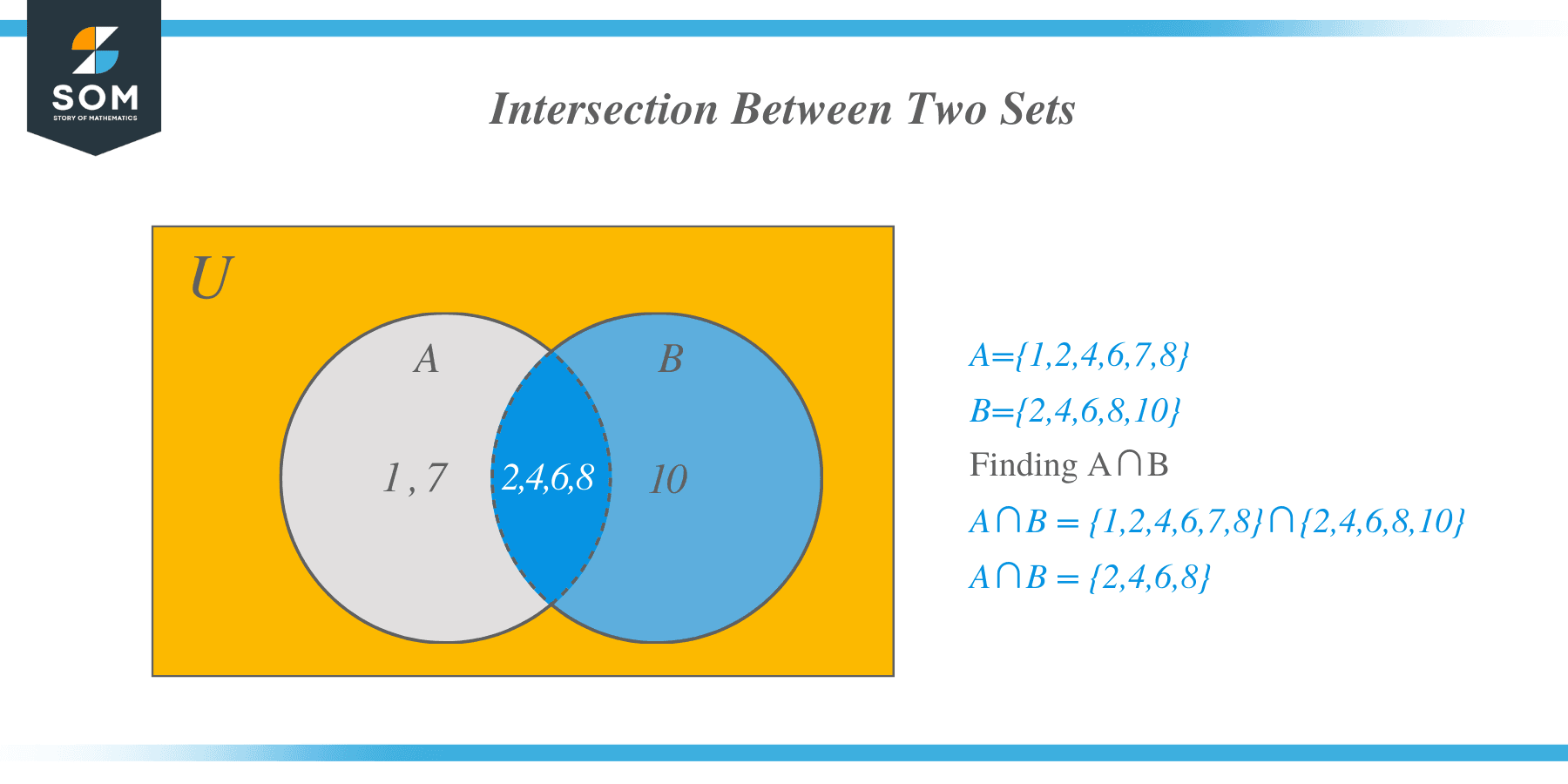
Example 1: Find out the intersection between the two sets.
$A$ = {$1,2,4,6,7,8$}
$B$ = {$2,4,6,8,10$}
Solution:
$A \cap B$ = {$1,2,4,6,7,8$} $\cap$ {$2,4,6,8,10$} = {$2,4,6,8$}
Example 2: Find out the intersection between the two sets.
$X$ = {$1,2,3,4,5,6$}$
$Y$ = {$\emptyset$}
Solution:
$X \cap Y$ = {$1,2,3,4,5,6$} $\cap$ {$\emptyset$} = {$\emptyset$}
We have discussed the intersection of two sets, but what if we have more than two sets? The process remains the same if we are dealing with two or more sets. For example, if we want to find out the intersection between three sets $X$, $Y$ and $Z$, then we will write the expression $X\cap Y \cap Z$. Let us now study some examples involving the intersection of three sets.
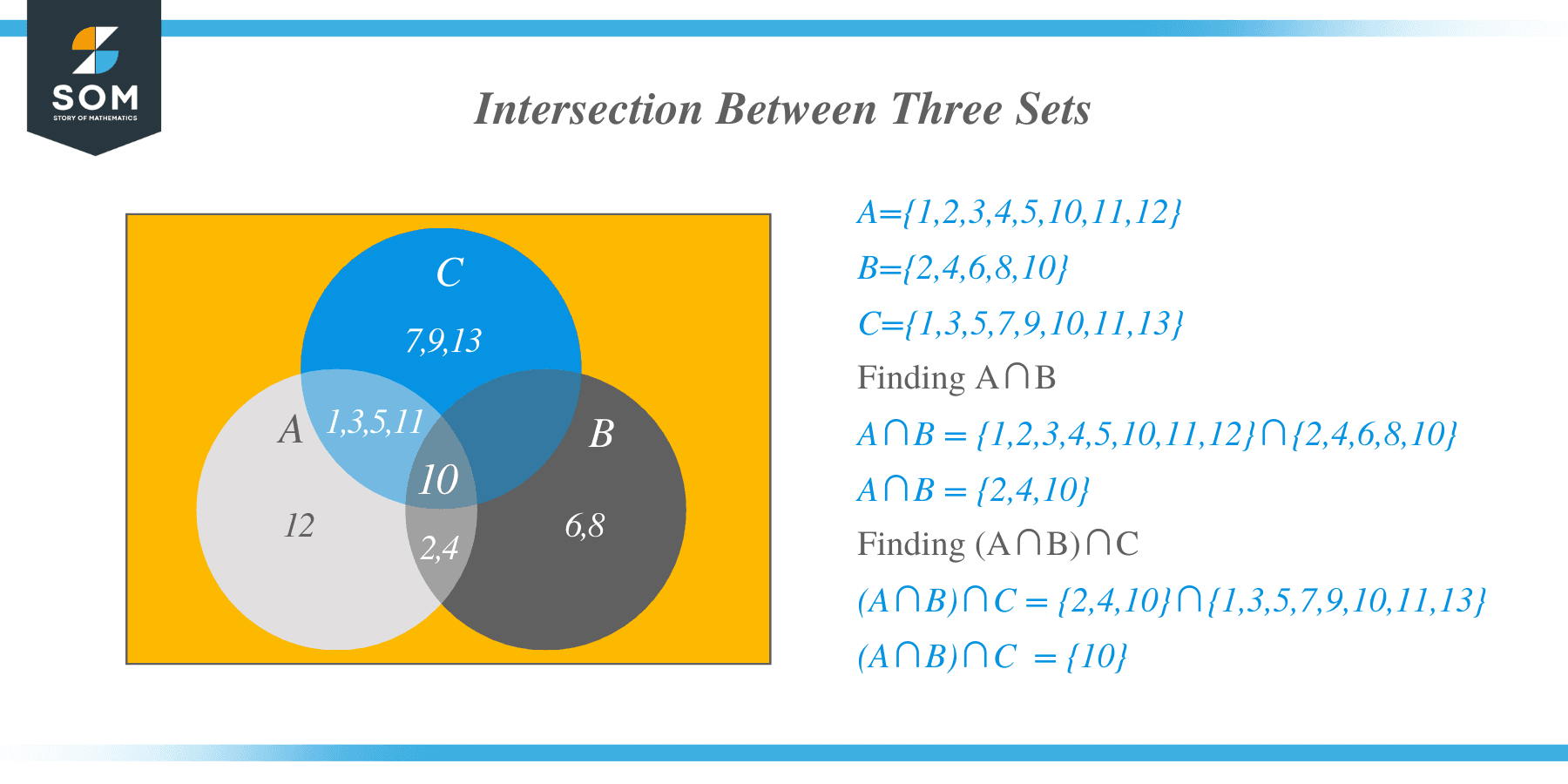
Example 3: Find out the intersection between the given sets.
$A$ = {$1,2,3,4,5,10,11,12$}
$B$ = {$2,4,6,8,10$}
$C$ = {$1,3,5,7,9,10,11,13$}
Solution:
We can directly solve it by doing the intersection of all the sets together, but the best approach is to solve it step by step. First, solve for $A \cap B$, then find the intersection for $A\cap B$ and C.
$A \cap B$ = {$1,2,3,4,5,10,11,12$} $\cap$ {$2,4,6,8,10$} = {$2,4,10$}
$A \cap B \cap C$ = {$2,4,10$} $\cap$ {$1,3,5,7,9,10,11,13$} = {$10$}
Example 4: Find out the intersection between the two sets.
$X$ = {$1,2,3,4,5,10,11,12$}
$Y$ = {$2,4,6,8,10$}
$Z$ = {$1,3,5,7,9,11,13$}
Solution:
$X \cap Y = {$1,2,3,4,5,10,11,12$} $\cap$ {$2,4,6,8,10$} = {$2,4,10$}
$X \cap Y \cap Z$ = {$2,4,10$} $\cap$ {$1,3,5,7,9,11,13$} = {$\emptyset$}
We can see that as there was no common element among all the three sets, hence the answer is an empty set.
Example 5: Find out the intersection between the three sets.
$X$ = {$1,2,3,4,5,6,7,9$}
$Y$ = {$6,7,9$}
$Z$ = {$\emptyset$}
Solution:
$X \cap Y$ = {$1,2,3,4,5,6,7,9$} $\ cap$ {$6,7,9$} = {$6,7,9$}
$X \cap Y \cap Z$ = {$6,7,9$} $\cap$ {$\emptyset$} = {$\emptyset$}
From this example, we can conclude that if any one of the sets is an empty set, then no matter how many elements the rest of the sets have, the intersection between such sets will always result in an empty set.
Properties of Upside Down U
Different properties of upside-down U or intersection, frequently used in solving set problems, are given below.
- Commutative property
- Distributive property
- Associative property
- Idempotent property
Commutative Property: According to commutative property, the intersection of Set A and Set B equals the intersection of Set B and Set A.
$A \cap B = B \cap A$
Example 6: For the sets given below, prove that $X \cap Y = Y \cap X$
$X$ = {$1,2,3,4$}
$Y$ = {$3,4$}
Solution:
$X \cap Y$ = {$1,2,3,4$} $\cap$ {$3,4$} = {$3,4$}
$Y \cap X$ = {$3,4$} $\cap$ {$1,2,3,4$} = {$3,4$}
Hence proved $X \cap Y = Y \cap X$
Distributive Property: The distributive property will involve three sets, and this property includes the concept of union and intersection. The distributive property for three sets, X, Y and Z, can be written as
$X \cap (Y \cup Z) = (X \cap Y) \cup (X \cap Z)$
Example 7: For the sets given below, prove that $X \cap (Y \cup Z) = (X \cap Y) \cup (X \cap Z)$.
$X$ = {$1,2,3,4,5,6,7,8,9$}
$Y$ = {$3,4,5,6,7,8$}
$Z$ = {$2,4,6,8$}
Solution:
Let us first solve the left-hand side:
$Y \cup Z$ = {$3,4,5,6,7,8$} $\cup$ {$2,4,6,8$} = {$2,3,4,5,6,7,8$}
$X \cap (Y \cup Z)$ = {$1,2,3,4,5,6,7,8,9$} $\cap$ {$2,3,4,5,6,7,8$} = {$2,3,4,5,6,7,8$}
Now solving the right-hand side:
$X \cap Y$ = {$1,2,3,4,5,6,7,8,9$} $\cap$ {$3,4,5,6,7,8$} = {$3,4,5,6,7,8$}
$X \cap Z$ = {$1,2,3,4,5,6,7,8,9$} $\cap$ {$2,4,6,8$} = {$2,4,6,8$}
$(X \cap Y) \cup (X \cap Z)$ = {$3,4,5,6,7,8$} $\cup$ {$2,4,6,8$} = {$2,3,4,5,6,7,8$}
Hence, proved $X \cap (Y \cup Z) = (X \cap Y) \cup (X \cap Z)$.
Associative Property: The associative property involves three sets, and it states that if we are given sets X, Y and Z, then:
$X \cap (Y \cap Z) = (X \cap Y) \cap Z$
Example 8: For the sets given below, prove that $X \cap (Y \cap Z) = (X \cap Y) \cap Z$.
$X$ = {$2,4,6,8,10,12,14,16$}
$Y$ = {$1,2,3,4,5,6,7,8,9,10$}
$Z$ = {$4,8,12,16,20$}
Solution:
Let us first solve the left-hand side:
$Y \cap Z$ = {$1,2,3,4,5,6,7,8,9,10$} $\cup$ {$4,8,12,16,20$} = {$4,8$}
$X\cap (Y \cap Z)$ = {$2,4,6,8,10,12,14,16$} $\cap$ {$4,8$} = {$4,8$}
Now solving the right-hand side:
$X \cap Y$ = {$2,4,6,8,10,12,14,16$} $\cup$ {$1,2,3,4,5,6,7,8,9,10$} = {$2,4,6,8,10$}
($X \cap Y) \cap Z$ = {$2,4,6,8,10$} $\cap$ {$4,8,12,16,20$} = {$4,8$}
Hence proved $X \cap (Y \cap Z) = (X \cap Y) \cap Z$
Idempotent Property: According to this property, if we take the intersection of Set X with itself, the result will be A itself, and we can write it as:
$X \cap X = X$
Example 9: If X = {$1,2,3,4$} then prove than $X \cap X = X$
Solution:
$X \cap X$ = {$1,2,3,4$} $\cap$ {$1,2,3,4$} = {$1,2,3,4$}
Upside Down U in Probability
The upside-down U symbol has applications in probability. It is used to solve probability-related problems for independent and dependent events. For example, if we are given two events, $A$ and $B$, and both are independent events, then the probability of occurrence of events $A$ and $B$ is given as:
$P ( A \cap B) = P(A). P(B)$
If the events A and B are dependent, then we can solve for $P(A \cap B)$ by using the following formula:
$P(A\cap B) = P(A|B). P(A)$
Let us see some numerical examples of the upside-down U symbol in math statistics and probability.
Example 10: A husband and wife work in the same company. The probability that both husband and wife will earn more than 2 million dollars in the next $5$ years is $0.75$ and $0.65$ respectively. Find the probability for the event when both of them are earning more than 2 million dollars in the next $5$ years.
Solution:
Let P(A) be the probability for the husband and P(B) for the wife:
$P(A) = 0.75$
$P(B) = 0.65$
So, the probability, when both are earning more than 2 million dollars in the next $5$ years, can be calculated as:
$P(A) \cap P(B) = P(A). P(B) = 0.75 \times 0.65 = 0.4875$
Example 11: Nina wants to purchase the candies from a nearby store. The probability of going to the shop is 40 %, and the probability of purchasing candies from the store is 35 %. What is the probability of Nina actually going to the store and buying the candies?
Solution:
$P(A|B) = 0.35$
$P(B) = 0.4$
$P(A) \cap P(B) = P(A). P(B) = 0.35 \times 0.4 = 0.14$
Practice Questions
1. Find $X \cap Y$ for the sets $X$ = {$\emptyset$}, Y = {$2,3,4,5$}
2. Find $X\cup( Y\cap Z)$ for the sets $X = {1,2}$, $Y = {2,4,6}$ and $Z = {1,2,3,4,5,6}$
3. You are given a deck of cards (52 cards). Event A draws a spade card, while event B draws a red card. You are required to determine $P( A \cap B)$.
Answer Key:
1).
$X \cap Y$ = {$\emptyset$} $\cap$ {$2,3,4,5$} = {$\emptyset$}
2).
$Y \cap Z$ = {$2,4,6$} $\cap$ {$1,2,3,4,5,6$} = {$2,4,6$}
$X \cup ( Y\cap Z)$ = {$1,2$} $\cap$ {$2,4,6$} = {$1,2,4,6$}
3).
The total number of cards is $52$ while we have $13$ spade cards in total, so the probability of event A is:
$P(A) = \dfrac{13}{52}$
There are 26 red cards in total as event B occurs after the occurrence of event A, so the remaining cards are 51, and as spade cards are black, so we have all 26 red cards to choose from, so the probability for event B is:
$P(B) = \dfrac{26}{51}$
$P(A\cap B) = P(B|A) . P(A)$
$P(A\cap B) = \dfrac{13}{52} . \dfrac{26}{51} = 0.127$ approx.
