JUMP TO TOPIC
 The right prism is a three-dimensional solid figure with parallel, similar-shaped polygons at the top and bottom, and these polygons are connected vertically at an angle of $90^{o}$.
The right prism is a three-dimensional solid figure with parallel, similar-shaped polygons at the top and bottom, and these polygons are connected vertically at an angle of $90^{o}$.
In this guide, we will learn what a solid figure is. What does a right prism mean, and what are its types, the formula for the surface area and volume of a right prism, and how to calculate the surface area and volume of a right prism? By the end of the guide, you will have enough knowledge to easily solve problems involving right prisms.
What Is a Right Prism?
A prism in which lateral faces of the solids are perpendicular to the base as well as to the plane of the top is known as a right prism. In such a prism, the angle between the connection point at the edges of the base and the top will always be $90^{o}$.
The right prism is different from a non-right prism, and one can easily distinguish between the two by just looking at the faces and edges of the solid. Any prism where the side faces form an angle other than $90^{o}$ with the end faces/surfaces is called a non-right prism, and the prism where side faces form an angle of $90^{o}$ with the end faces is a right-prism.
Structure of a Right Prism
The structure of a right-prism consists of several attributes. The first one to consider is the number of side faces. For example, a square prism will have four end faces on the sides and two end faces (one at the bottom and one at the top), so the square prism’s total number of faces will equal six.
It would be best if you distinguished between the end faces and the side faces of the prism. The side faces cover the lateral area of the prism only, while the base and the top surface along with the side faces form the total surface area of the prism.
Depending upon the shape of the faces, we get different prisms. Let’s discuss these types of prisms.
Types of a Right Prism
There are many different types of right prisms, and some of the important ones are given below:
- Right rectangular prism
- Square or cubic prism
- Triangular prism or right triangular prism
- Cylinder
Right Rectangular Prism: A right-rectangular-prism is a 3-dimensional solid figure having six faces with 8 vertices and 12 edges. All the faces of the right-rectangular-prism will be rectangular, and all angles are $90^{0}$. The right-rectangular prism is also called a cuboid.
The formula for surface area and volume of a right-rectangular-prism is given below.
Surface Area $= 2(length. height + width.height.+ length.width)$
Volume $= Length \times height \times width$
Right Square Prism: A right-square prism or a cube is a 3-dimensional solid figure, and just like the right rectangular prism, it has six faces with 8 vertices and 12 edges. All faces of the cube or right square prism will be square in shape, and angles are all equal to $90^{0}$ each. The right square prism is also called a cube. The formula for surface area and volume of a right square prism is given below:
Surface Area of a right square prism or cube $= 6.a^{2}$
Where “a” is the length of one side of a square.
The volume of a right square prism or cube $= a^{3}$
Triangular Prism or Right Triangular Prism: A triangular prism is a three-dimensional solid figure which consists of a triangular base and a triangular top. If the base and the top are right triangles, it will be called a right triangular prism. A triangular prism has five faces with six vertices and nine edges.
If both the triangles at the top and bottom do not have an angle of $90^{0}$ while vertices are connected at $90^{0}$, then it will be called a triangular prism.
Remember, both triangular and right triangular prism are types of a right prism as the lateral faces of both solids have an angle of $90^{0}$ or all the lateral faces are perpendicular to the plane of the base and the top.
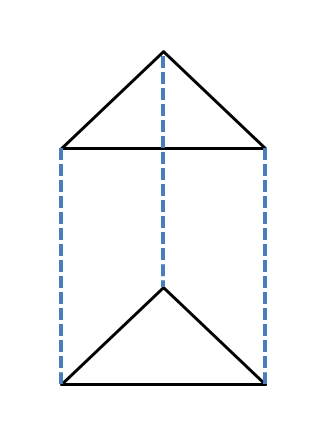
The formula for surface area and volume of a triangular prism will depend upon the type of triangle we are given, but we can write the general formula as:
Surface area of the triangular prism $= Area\hspace{1mm} base \times height$
Volume of the triangular prism $= \dfrac{1}{2}\times base \times height$
Cylinder: Is a cylinder a right prism? The answer is yes, a cylinder is also a type of right prism as the base and the top of a cylinder are circles, and both these circles are connected at an angle of $90^{0}$, thus making the cylinder a right prism. we can write the formula for the surface area and volume of a cylinder as:
T.S.A of cylinder $= 2\pi.r.h + 2\pi.r^{2}$
Area of the side $= 2\pi.r.h$
Area of the base $= \pi.r^{2}$
Area of the top $= \pi.r^{2}$
Volume of the cylinder $= \pi.r^{2}.h$
Lateral Surface Area and Volume of a Right Prism
In the right prisms, we are more interested in finding the figure’s lateral surface area as the right prism’s lateral faces are perpendicular to the base plane and the top of the solid. Many problems only require calculating the lateral surface area of the figure, and the lateral surface area excludes the surface area of the base and top of the prism.
Consider the figure below. Here, the top and base of the prism are triangles that are colored orange, while the lateral surface area is the white region between these two triangles.
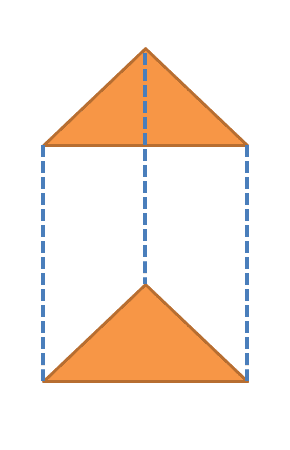
This whole white region is called the lateral surface area, and we can write the formula for the lateral surface area as:
Lateral Surface area ( L.S.A) $= Perimeter \hspace{1mm} of \hspace{1mm} base \times height\hspace{1mm} of\hspace{1mm} the\hspace{1mm} prism$
The total surface area of the right prism will include the surface area of the top and bottom figure while also including the lateral surface area. For example, suppose we want to calculate the total surface area of the above figure. In that case, we will add the bottom and top surface area of both triangles to the lateral surface area, giving us the total surface area of the right prism.
The formula for the total surface area can be given as:
Total surface area $= L.S.A + 2 ( Area\hspace{1mm} of\hspace{1mm} the\hspace{1mm} base)$
For the figure above, we know that the base and top are triangles, so the formula for the total surface area is written as:
T.S.A for triangular prism $= L.S.A + 2 (\dfrac{1}{2}.b.h)$
T.S.A for triangular prism $= L.S.A + (b.h)$
The right prism volume is calculated just like we calculate the volume of any solid figure. We multiply the base area with the height of the prism. We can write the right prism formula for the volume as:
Volume of the right prism $= Base \hspace{1mm}area \times height\hspace{1mm} of\hspace{1mm} the\hspace{1mm} prism$
Difference Between the Right Prism and Other Solids
It is easier to get confused between some solids and the right prisms. In this section, we will compare two right prisms which students often mix up.
Triangular Prism and a Pyramid: A triangular prism or a right triangular prism consists of two bases. The faces of both end surfaces or the edges of the surfaces are parallel. On the other hand, the pyramid only consists of a single base, and all points of the base are connected at a single vertex point.
Square Prism and Cuboid: The square prism base and top surface consist of a square and all the faces of the square prism also form a square; on the other hand, a cuboid is a rectangular prism with the base having a rectangular shape. The top and base of the cuboid have two parallel and congruent sides, just like a rectangular prism.
Examples of Right Prisms
Let us now study various examples related to right prisms.
Example 1: Anna wants to build a cardboard box (without the lid). Anna has worked out the required dimensions of her box. The box should be 5 units long, 7 units wide, and 8 in height. Help Anna determine the amount of cardboard she should buy.
Solution:
We can determine the surface area of the box by using the formula:
Surface area $= 2( Length. Width + Width. height + Length.height)$
Surface area $= 2 (5\times 7\hspace{1mm} +\hspace{1mm}7\times 8 \hspace{1mm}+ \hspace{1mm}5\times 8) = 2 ( 35\hspace{1mm} +\hspace{1mm} 56 +\hspace{1mm} 40) = 262\, unit^{2}$
So Anna should buy $262 unit^{2}$ of cardboard to build the box without the lid.
Example 2: Suppose you are given a rectangular prism. The base area of the rectangular prism is $25 cm^{2}$ while the volume of the prism is $50 cm^{2}$. What will be the height of the prism?
Solution:
We know that the formula for the volume of a prism is given as:
Volume $= base \hspace{1mm}area \times height\hspace{1mm} of\hspace{1mm} the\hspace{1mm} prism$
We are given the volume and base area of the prism.
$50 = 25 \times height$
$h = \dfrac{50}{25} = 2 cm$
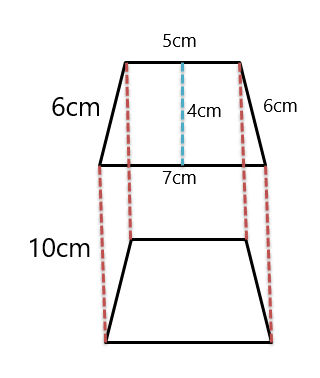
Example 3: In the figure below, you are given a trapezoidal prism and you are required to determine the lateral surface area, right prism surface area, and the volume of the trapezoidal prism.
Solution:
We know we can write the formula for the lateral surface area of a prism as:
Lateral Surface area ( L.S.A) $= Perimeter \hspace{1mm}of\hspace{1mm} base \times h$
Here, “h” is the altitude of the right prism.
So the height of the prism is given as $10 cm$.
To get the perimeter of a trapezoid, we add up all the sides of the trapezoid.
Perimeter $= 6\hspace{1mm} +\hspace{1mm} 6 \hspace{1mm}+ 6\hspace{1mm} +\hspace{1mm} 7 = 25 cm$
L.S.A $= 25 \times 10 = 250 cm^{2}$
We know the formula for total surface area is given as:
Total surface area $= L.S.A + 2 (Area\hspace{1mm} of\hspace{1mm} the\hspace{1mm} base)$
So we have to find the area of the trapezoid first to solve for T.S.A.
We can write the formula for the area of the base as:
Area $= \dfrac{1}{2}(a+b).h$
Where “a” is the length of three similar sides while “b” is the length of a side that is different from the rest and “h” is the height of the trapezoid.
Area $= \dfrac{1}{2}(6+7).4$
Area $= 2 (13) = 26 cm^{2}$
Total surface area (T.S.A) $= 250 + 2(26) = 250 + 52 = 302 cm^{2}$
Finally, we we determine the volume of the trapezoidal prism.
We know the volume formula for a prism is given as:
Volume $= Base \hspace{1mm}area \times height\hspace{1mm} of \hspace{1mm}the\hspace{1mm} prism$
Volume $= 26 \times 10 = 260 cm^{3}.$
Important Definitions
Surface Area of a Solid: The surface area or total surface area of the solid is the area enclosed within all the solid surfaces. It means that the area is within all the side faces and end faces of the solid. The unit of the surface area is given as $unit^{2}$.
The volume of a Solid: The volume of the solid is the total space taken up by the solid, and if we are given a composite solid, then we add the volume of all figures to get the total volume. The unit of a volume is given in $units^{3}$.
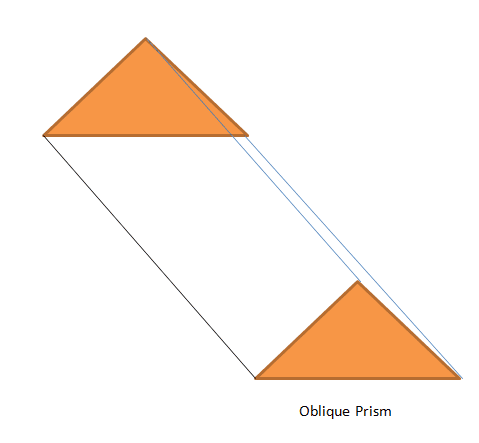
Oblique Prism And Right Prism: The prism where the end surfaces or bases are parallel to each other but their edges do not form an angle of $90^{0}$ and the top surface is not exactly on the top of the base surface; hence the height of the prism is tilted outside the prism. In the right prism with two triangular end surfaces, all lateral faces will form a rectangle, while in the oblique prism, the bases are not exactly one over another, so its vertices will not form the angle of $90^{o}$.
Practice Questions:
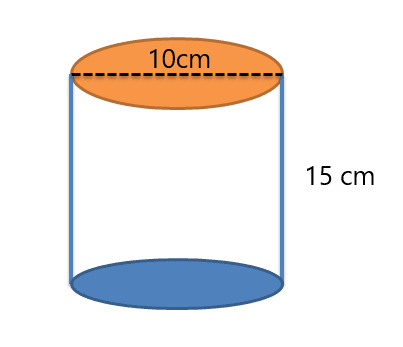
1. Correctly determine the surface area and volume of the cylinder given below.
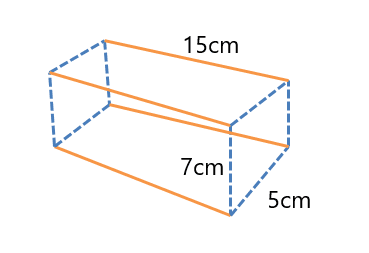
2. William has bought a gift for his friend, and the shape of the gift is given below. Help William calculate the area of the gift paper required to cover the whole box ( there is no overlapping of gift papers on the corners of the box).
Answer Keys:
1).
The formula for total surface area of the cylinder is:
T.S.A of cylinder $= 2\pi.r.h + 2\pi.r^{2}$
The radius will be $= \dfrac{10}{2}= 5cm$
Height of the cylinder = 15 cm
T.S.A $= (2\pi.5.15) + 2\pi.5^{2} = 150\pi + 50\pi = 150\pi cm^{2}$
Volume of the cylinder $= \pi.r^{2}.h = \pi.5.15 = 75\pi cm^{3}$
2).
We only need to determine the surface area of the rectangular box (gift); this gives us the value for the gift wrapper required to cover it.
Surface area $= 2( Length. Width + Width. height + Length.height)$
S.A $= 2 (5\times 15\hspace{1mm} + \hspace{1mm}15\times 7 \hspace{1mm}+ \hspace{1mm}5\times 7)$
S.A $= 2 ( 75\hspace{1mm} + \hspace{1mm}105 +\hspace{1mm} 35) = 430 cm^{2}$
So we need wrapping paper that has an area of $430cm^{2}.$
