
- What is the electric potential at the point on the x-axis where the electric field is zero?
- What are the magnitude and direction of the electric field at the point on the x-axis, between the charges, where the electric potential is zero?
Expert Answer:
Two point charges $q_1$ and $q_2$ are present on the $x-axis$ with $-10 nC$ and $20 nC$, respectively. Assuming $q_1$ on the origin and $q_2$ is $15 cm$ apart from it, the electric potential due to two point charges is given as:\[ V = V_1 + V_2 \]Where $V_1$ and $V_2$ are given as:\[ V_1 = k \dfrac{q_1}{r} \]\[ V_2 = k \dfrac{q_2}{15 – r} \]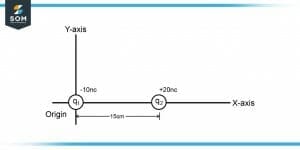
Figure-1 : Depiction of Charges
a) We need to find the electric potential at the point on $x-axis$ where the electric field is zero. We can equate the potentials due to both point charges to get the point on $x-axis$.
\[ \dfrac{k |q_1|}{r^2} = \dfrac{k q_2}{(15 – r)^2} \]
\[ \dfrac{|q_1|}{r^2} = \dfrac{q_2}{(15 – r)^2} \]
\[ |q_1|(15 – r)^2 = q_2 r^2 \]
By substituting and solving the equation, we get:
\[ r = [6.21 cm , -36.21 cm] \]
We know that at $r=6.21 cm$, the electric field can not be zero. So at $r=-36.21 cm$ the electric field is zero on the $x-axis$ as the point shown in Figure 2. Now to find the electric potential at this point, we need to substitute the values in the equation defined above, which is given as:
\[ V = k \dfrac{|q_1|}{r} + k \dfrac{q_2}{15 – r} \]
Here $k$ is the constant and its value is given as:
\[ k = 9 \times 10^9 N.m^2/C^2 \]
Substituting the values of $q_1, q_2, k, \text{and} r$ we get:
\[ V = 9 \times 10^9 N.m^2/C^2 \big{[} \dfrac{10 \times 10^{-9}C}{-36.21 cm} + \dfrac{20 \times 10^{-9}C}{15 – (-36.21 cm)} \big{]} \]
Simplifying the equation, we get:
\[ V = 103 V \]
b) The point where the electric potential is zero can be calculated by the equation of electric potential by equating it to zero. The equation is given as:
\[ V = V_1 + V_2 \]
By putting $V=0$, we can find the point where the electric potential is zero between two oppositely charged point charges.
\[ 0 = k \dfrac{q_1}{r} + k \dfrac{q_2}{15 – r} \]
\[ – k \dfrac{q_1}{r} = k \dfrac{q_2}{15 – r} \]
\[ – q_1(15 – r) = q_2 r \]
\[ r = -15 (\dfrac{q_1}{q_2 – q_1}) \]
By substituting the values, we get:
\[ r = 5 cm \]
Now we simply substitute the values in the equation to calculate the magnitude of electric field at $r=5 cm$. Equation is given as:
\[ E = E_1 + E_2 \]
\[ E = k \dfrac{|q_1|}{r^2} + k \dfrac{q_2}{(15 – r)^2} \]
Substituting the values and solving the equation, we get:
\[ E = 54 \text{$kV/m$} \]
The direction of the electric field will be in the direction of the vector sum of the given two point charges $\overrightarrow{E_1}$ and $\overrightarrow{E_2}$. The direction of the electric field will be from $q_2$ towards $q_1$, which is towards negative $x-axis$.
Numerical Results:
a) The electric potential on the point where the electric field is zero on the $x=axis$ is:
\[ V = 103 V \]
b) The magnitude of the electric field on the point where the electric potential is zero on $x-axis$ is:
\[ E = 54 \text{$kV/m$} \quad \text{Its direction will towards negative $x-axis$} \]
Example:
A $-5 \mu C$ point charge and a $5 \mu C$ point charge are $7 cm$ apart from each other. Find the electric field given by these point charges at the mid-point between these charges.
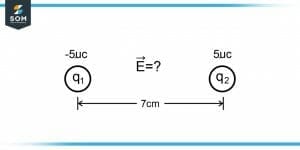
Figure-2 : Point Charges
The electric field is given by,
\[ E = E_1 + E_2 \]
\[ E = k \Big{[} \dfrac{ 5 \times 10^{-6} C}{3.5 cm} + \dfrac{ 5 \times 10^{-6} C}{3.5 cm} \Big{]} \]
\[ E = 9 \times 10^{9} Nm^2/C^2 \Big{[} \dfrac{ 5 \times 10^{-6} C}{3.5 cm} + \dfrac{ 5 \times 10^{-6} C}{3.5 cm} \Big{]} \]
By solving it, we get:
\[ E = 2.6 \times 10^6 N/C \]
Images/Mathematical drawings are created with Geogebra.
