This question aims to learn the basic methodology for optimizing a mathematical function (maximizing or minimizing).
Critical points are the points where the value of a function is either maximum or minimum. To calculate the critical point(s), we equate the first derivative’s value to 0 and solve for the independent variable. We can use the second derivative test to find maxima/minima. If the value of $V’’(x)$ at the critical point is less than zero, then it’s a local maximum; otherwise, it’s a local minimum.
Expert Answer
Let $x$, $y$, and $y$ be the dimensions of the rectangular box as shown in figure 1 below:
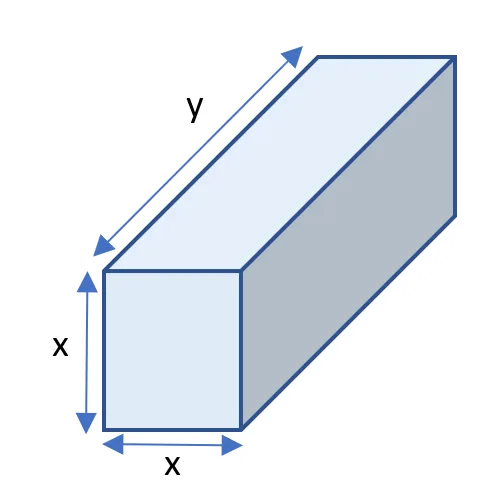Figure 1
Follow the steps to solve this question.
Step 1: Calculate perimeter $P$:
\[ P = x + x + x + x + y \]
\[ P = 4x + y \]
Given that, $P = 108$
\[y = 108 – 4x\]
Step 2: Calculate Volume of the box $V(x)$:
\[ V(x, y) = x \cdot x \cdot y \]
\[ V(x, y) = x^2 y\]
Substituting value of $y$:
\[ V(x) = x^2 (108 – 4x) \]
\[ V(x) = 108x^2-4x^3 \]
Step 3: Find the first and second derivatives:
\[ V’(x) = 2(108x)-3(4x^2) \]
\[ V’(x) = 216x-12x^2 \]
\[ V’’(x) = 216 – 2(12x) \]
\[ V’’(x) = 216 – 24x \]
Step 4: At critical point(s), $V(‘x) = 0$:
\[ 216x – 12x^2 = 0 \]
\[ x (216 – 12x) = 0 \]
This implies that either $x = 0$ or $216-12x = 0 \rightarrow x = \frac{216}{12} \rightarrow$ $x = 18$.
Step 5: Perform a Second derivative test:
Find $V’’(x)$ at $x = 18$ and $x = 0$,
\[ V’’(0) = 216 – 24(0) = 216 > 0 \rightarrow minima \]
\[ V’’(18) = 216 – 24(18) = -216 < 0\rightarrow maxima \]
Hence, volume $V$ is maximum at $x = 18$
Step 5: Final dimensions of the box:
\[ y = 108 – 4(18) \]
\[ y = 36 \]
Numerical Result
The maximum volume of the box is calculated as $18$ x $18$ x $36$ for the values of $x$, $y$ and $z$, respectively.
Example
A rectangular package to be sent by a postal service that has a maximum total length and perimeter (or girth) limit of $54$ inches. A rectangular package is to be sent via this service. Calculate the dimensions of the package that covers the maximum volume (Cross-sections may be assumed to be square).
\[P = 54 = 4x + y\]
\[y = 54 – 4x\]
\[V(x,y) = x^2 y = x^2 (54 – 4x) = 54x^2-4x^3\]
\[V’(x) = 108x – 12x^2 = 0\]
This implies:
\[x = 0 \ or\ x = 9\]
\[V’(x) = 108x – 12x^2 = 0\]
Since:
\[ V’'(x) = 108 – 24x \]
\[ V’'(9) = 108 – 24(9) = -108 > 0 \]
Maximum dimensions are $x = 9$ and $y = 108 – 4(9) = 72 $.