What is d/dx? A Detailed Explanation

The symbol d/dx is used to differentiate any function with respect to the variable $x$.

The derivative or differentiation in mathematics is used to determine the rate of change of a given function. So, if we are using the d/dx formula or the d/dx symbol with a function “$f$,” then we are calculating the rate of change of function “$f$” with respect to the variable “$x$”. In this guide, we’ll explain everything you need to know about this concept and give detailed examples.

What Is d/dx?

d/dx is an operator that means to differentiate any function with respect to variable $x$. You will come across questions like “How to pronounce d/dx?” or “What does d/dx stand for?” We can define $\dfrac{d}{dx}$ as the rate of change of a given function with respect to the independent variable “$x$”. It is pronounced as “Dee by dee ex.”

Defining d/dx

While studying differential equations, you will come across d/dx vs dy/dx. So what is the difference between these two terms? If we write $\dfrac{d}{dx}$ as $\dfrac{dy}{dx}$, then this means that we are differentiating dependent variable “$y$” with respect to independent variable “$x$”.

We use the process of differentiation when we are dealing with a function with a varying independent variable; this means the variable is dynamic and it changes its value, so we are dealing with the rate of change, and to solve such problems, we use derivatives or $\dfrac{d}{dx}$. So, we can say that $\dfrac{d}{dx}$ is used to evaluate the sensitivity between the dependent and independent variables.

Differentiation has vast applications in the field of engineering, sciences and technology as scientists often deal with problems that require observation of the rate of change concerning different variables, and they have to use derivatives and anti-derivatives to obtain the final form of the function to assess the behavior of the system under certain conditions.

Slope, Limit and d/dx

The slope of a function is the same as its derivative. For example, if we give a function “$y=f(x)$”, then the slope of this function is the rate of change of the “$y$” with respect to “$x$”, which is the same as $\dfrac{d}{dx}$. 

Let us consider the graph below.

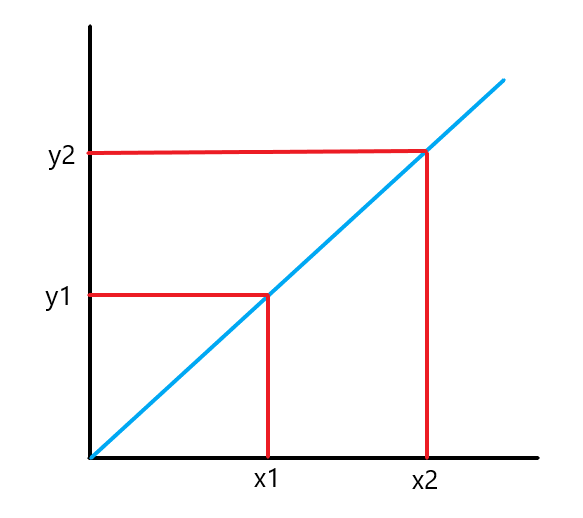
We can determine the derivative of the function by using the slope of a tangent line at a given point. The slope for a function “$y=f(x)$” is the ratio of the rate of change in the variable “$y$” to the rate of change of variable “$x$” So, we can write the formula for the slope of a straight line as

Slope = $\dfrac{y_2 \hspace{1mm} – \hspace{1mm}y_1}{x_2\hspace{1mm} – \hspace{1mm}x_1}$

We know that functions are not always straight lines; functions can be non-linear. As a matter of fact, most of the functions we deal with in maths or in real life are non-linear functions. So, how do we find the slope of a curve? The slope of a curve is determined by using the process of limits, and the same process is used to determine formulas for d/dx of various functions.

For a non-linear function, the ratio of change in the variable “$y$” with respect to changes in available “$x$” will be different for different values of $x$. To calculate the slope of the curve, we will draw a chord and then choose the desired point where we draw the tangent of the slope. So, we will have two points, and the demonstration is presented in the graph below.

When we want to determine the slope for a curve at a given point, then the selection or calculation for the second point needs some attention. We do not fix the position of the second point — on the contrary, we use it as a variable and call it “$h$”.

We are looking at the smallest possible change (since we are interested in finding the slope at one point so the second point is taken with the smallest possible change) so we put a limit of h approaching zero. So if the function is $f(x)$, then the second point function will become $f(x + h)$. The steps to determine the derivative of a curve can be written as:

1. Take the first point $(x,f(x))$ and for the second point change the value of “$x$” as “$x + h$” so the function for the second point is $f(x + h)$
2. The rate of change of functions will be $f(x \hspace{1mm}+ \hspace{1mm}h) – f(x)$
3. Applying the limit where “$h$” approaches zero to obtain the derivative of the curve

$\dfrac{df}{dx} = \lim_{h \to 0} \dfrac{f(x\hspace{1mm} +\hspace{1mm} h) -\hspace{1mm} f(x)}{h}$

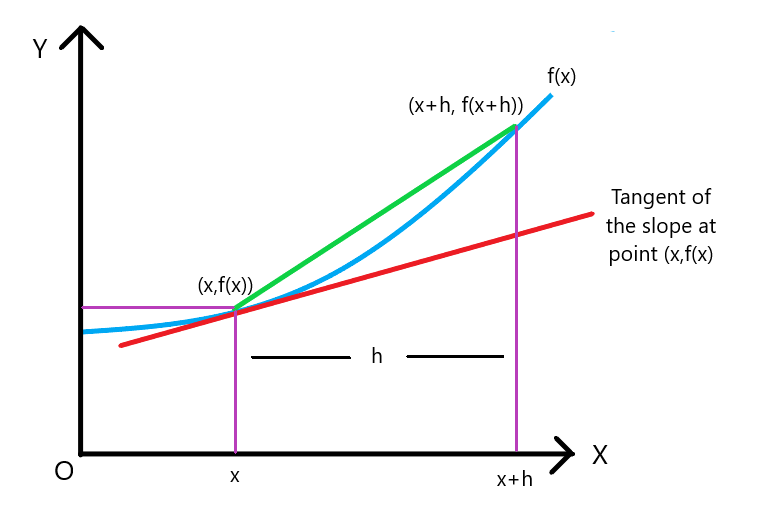
Formulas for d/dx

The symbol $\dfrac{d}{dx}$ or the derivative has specific formulas for linear, non-linear, exponential and logarithmic functions, and these formulas are the basis for solving differential equations. Some of the formulas are given below.

1. $\dfrac{d}{dx} c = 0$ Here “c” is a constant
2. $\dfrac{d}{dx} x = 1$
3. $\dfrac{d}{dx} cx = c$
4. $\dfrac{d}{dx} x^{k} = k.x^{k-1}$
5. $\dfrac{d}{dx} e^{x} = e^{x}$
6. $\dfrac{d}{dx} a^{x} = a^{x} . log_{a}$
7. $\dfrac{d}{dx}\sqrt{x} = \dfrac{1}{2}. \sqrt{x}$

The derivative formula is also used for trigonometric functions; some of the derivatives of the trigonometric functions are given below.

1. $\dfrac{d}{dx} cos(x) = -sin(x)$
2. $\dfrac{d}{dx} sin(x) = cos(x)$
3. $\dfrac{d}{dx} tan(x) = sec^{2}(x)$
4. $\dfrac{d}{dx} cosec(x) = -cosec(x).cot(x)$
5. $\dfrac{d}{dx} sec(x) = sec(x).tanx(x)$
6. $\dfrac{d}{dx} cot(x) = -cosec^{2}(x)$

Applications of d/dx

The derivative or $\dfrac{d}{dx}$ has various applications in pure mathematics and in real life as well. In mathematics, when we are asked to find the slope of a curve or we need to optimize a function and want to determine the maxima or minima of the function or to apply a chain rule, we use derivatives. Some of the applications of derivative or $\dfrac{d}{dx}$ in mathematics are given below.

1. To determine whether a function is increasing or decreasing
2. Determining the rate of change of a function
3. Finding out the maxima and minima of a non-linear function
4. Finding out the slope and tangent of a curve
5. It is used to solve higher-order derivatives
6. Finding out the normal of a curve
7. Determining the approximate value of the function

Now, let us look at some real-life examples of $\dfrac{d}{dx}$ or derivative.

1. The derivative can be used to determine the change in temperature, pressure or any other quantity.
2. Derivatives are used to determine the velocity, acceleration and distance covered.
3. Derivatives are used in first and second-order differential equations, which in turn are used in many engineering applications.
4. Derivatives are used by businessmen for the calculation of profits and losses or variation of profits and losses in a business.
5. Derivatives are used to determine changes in weather patterns, and in the field of seismology, they are used to determine earthquake magnitudes.

Let us now study some examples related to $\dfrac{d}{dx}$, so you can see its applications while solving different problems.

Example 1: What is d/dx of  50?

Solution

The number 50 is a constant, so its derivative is zero.

Example 2: What is d/dx 1/x?

Solution

$\dfrac{d}{dx} \dfrac{1}{x} = -\dfrac{1}{x^{2}}$

Example 3: Determine the derivative of the function $f(x) = 3x \hspace{1mm}+ \hspace{1mm}9$

Solution

We are given the function $f(x) = 3x \hspace{1mm}+ \hspace{1mm}9$

Now taking the derivative on both sides

$\dfrac{d}{dx} f(x) = \dfrac{d}{dx} [3x \hspace{1mm}+ \hspace{1mm}9]$

$\dfrac{d}{dx} f(x) = \dfrac{d}{dx}3x + \dfrac{d}{dx} 9$

$\dfrac{d}{dx} f(x) = 3(1) + 0 = 3$

Example 4: Determine the derivative of the function $f(x) = 2x^{2}\hspace{1mm} + 6x\hspace{1mm} – \hspace{1mm}2$

Solution

We are given the function $f(x) = 2x^{2}\hspace{1mm} +\hspace{1mm} 6x\hspace{1mm} – \hspace{1mm}2$

Now taking the derivative on both sides

$\dfrac{d}{dx} f(x) = \dfrac{d}{dx} [2x^{2} + 6x – 2]$

$\dfrac{d}{dx} f(x) = \dfrac{d}{dx}2x^{2} + \dfrac{d}{dx} 6x – \dfrac{d}{dx} 2$

$\dfrac{d}{dx} f(x) = 2.2 x \hspace{1mm}+ \hspace{1mm}6(1) – \hspace{1mm}0 = 4x\hspace{1mm} +\hspace{1mm}6$

Example 5: Determine the derivative of the function $f(x) = 4 tanx + 3$

Solution

We are given the function $f(x) = 4 tanx \hspace{1mm}+ \hspace{1mm}3x $

Now taking the derivative on both sides

$\dfrac{d}{dx} f(x) = \dfrac{d}{dx} [4 tanx + 3x]$

$\dfrac{d}{dx} f(x) = \dfrac{d}{dx}4 tanx + \dfrac{d}{dx} 3x$

$\dfrac{d}{dx} f(x) = 4 sec^{2}x + 3$

Example 6: Determine the derivative of the function $f(x) = 3x^{3}\hspace{1mm} + \hspace{1mm}6x^{2} – \hspace{1mm}5x$

Solution

We are given the function $f(x) = 3x^{3} + 6x^{2} – 5x$

Now taking the derivative on both sides

$\dfrac{d}{dx} f(x) = \dfrac{d}{dx} [3x^{3} + 6x^{2} – 5x]$

$\dfrac{d}{dx} f(x) = \dfrac{d}{dx}3x^{3} + \dfrac{d}{dx} 6x^{2} – \dfrac{d}{dx} 5x$

$\dfrac{d}{dx} f(x) = 3\times 3 x^{2} + 6\times 2 x – \dfrac{d}{dx} 5(1) = 9x^{2} + 12x – 5$

Frequently Asked Questions

What Does d by dx Stand For?

There is no exact abbreviation for the symbol $\dfrac{d}{dx}$, but in general, we say d by dx means differentiating with respect to “$x$”. The first “$d$” or the numerator “$d$” is just differentiation and if we put “$y$” or $f(x)$ in front of it, then we will say differentiate function “$y$” with respect to “$x$”.

What Is Derivative of 1?

The derivative of any constant is zero. As “$1$” is a constant number, hence derivative of “$1$” is zero.

Conclusion

Let us conclude our topic by revisiting some of the essential points we have discussed regarding $\dfrac{d}{dx}$.

• The symbol or the notation d/dx is taking derivative with respect to independent variable “x.”
• When we want to differentiate any function, then we just place d/dx prior to a function. For example, for the function f(x) = y = 3x, we will differentiate the function “y” with respect to “x” by using dy/dx
• d/dx is used to define the rate of change for any given function with respect to the variable “x”.