JUMP TO TOPIC
 The $\triangle$ ABC is similar to $\triangle$ DEF when the corresponding sides of both triangles are in proportion to each other and the corresponding angles are the same as well.
The $\triangle$ ABC is similar to $\triangle$ DEF when the corresponding sides of both triangles are in proportion to each other and the corresponding angles are the same as well.
We should keep in mind that the shape of both the triangles will be the same, but their size may vary. In this article, we will discuss when two triangles are similar, along with numerical examples.
What Does Triangle ABC Is Similar to Triangle DEF Mean?
The term similar triangles means that both triangles are similar in shape but can vary in size, which means that the size or length of the sides of both triangles may vary, but the sides will remain in the same proportion.
The second condition for both triangles to be similar is that they must have congruent or equal angles. Similar triangles are different from congruent triangles; for similar triangles, the shape is the same, but the size may vary, whereas, for congruent triangles, both size and shape must be the same. So the properties of similar triangles can be summarized as:
- The triangles must have the same shape, but the size can differ.
- The corresponding angles of both triangles are the same.
- The ratio or proportion of the corresponding sides of both triangles should be the same.
A similar symbol is written as “ $\sim$. “
Similarity Theorems for Triangles
We can prove the similarity of triangles by using different similarity theorems. We use these theorems depending upon the type of information we are provided. We do not always get the lengths of each side of the triangle. In some cases, we are only provided with incomplete data, and we use these similarity theorems to determine whether or not the triangles are similar. The three types of similarity theorems are given below.
- A.A or Angle-Angle Similarity Theorem
- SAS or Side-Angle-Side Theorem
- S.S.S Side-Side-Side Theorem
Angle-Angle Similarity Theorem
The AA or Angle Angle similarity theorem states that if any two angles of a given triangle are similar to two angles of another triangle, those triangles are similar. Let us compare two triangles, ABC and DEF. ABC has three angles $\angle A$, $\angle B$ and $\angle C$. Similarly, the triangle DEF has three angles $\angle D$, $\angle E$ and $\angle F$. So, according to A. A theorem is if any of the two angles of ABC are equal to any two angles of DEF, then these triangles are similar.
We will use this theorem when we are not provided with the length of the sides of the triangles and we only have angles of the triangles. Suppose, $\angle A$ is equal to $\angle D$, i.e., $\angle A = \angle D$ and $\angle B = \angle E$, then by A.A similarity postulates both these triangles are the same.
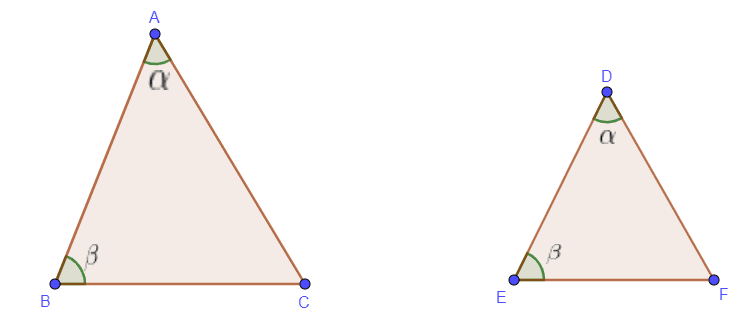
Hence $\triangle$ ABC $\sim \triangle$ DEF, and as both these triangles are similar; we can state that the corresponding sides of both triangles are also proportional to each other, i.e.,
$\dfrac{AB}{DE} = \dfrac{AC}{DF} = \dfrac{BC}{EF}$
Side-Angle-Side Similarity Theorem
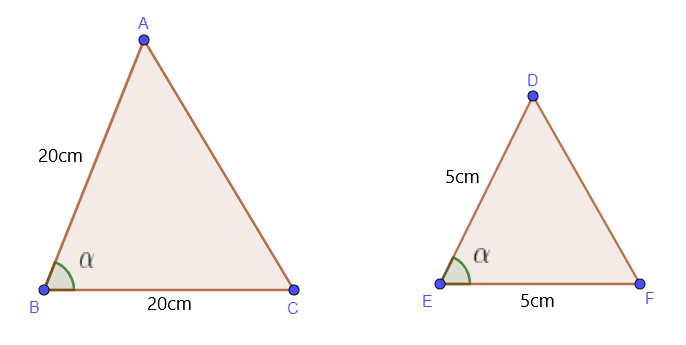
The SAS or side angle side theorem states that if two sides of a given triangle are similar to two sides of another triangle and simultaneously if one angle of both the triangles is equal, then we will say that both these triangles are similar to each other.
We use this theorem when we are given the lengths of two sides and one angle of the triangles. Suppose we are given the length of two sides AB and BC of $\triangle$ ABC along with the value of $\angle B$. The $\triangle$ ABC will be similar to $\triangle$ DEF under the following conditions:
$\dfrac{AB}{DE} = \dfrac{BC}{EF}$, and $\angle B = \angle E$
Or
$\dfrac{AB}{DE} = \dfrac{AC}{DF}$, and $\angle A = \angle D$
Or
$\dfrac{AC}{DF} = \dfrac{BC}{EF}$, and $\angle C = \angle F$
Side-Side-Side Similarity Theorem
The SSS or Side-Side-Side theorem states that if the proportion or ratio of corresponding sides of two triangles is similar, then such triangles are always similar. We will use this theorem when the length of all the sides of both triangles is provided. If we are given the measurement of sides of $\triangle$ ABC and $\triangle$ DEF, then they will both be similar to each other if:
$\dfrac{AB}{DE} = \dfrac{BC}{EF}= \dfrac{AC}{DF}$
Example 1
From the given data, determine whether $\triangle$ ABC is similar to $\triangle$ DEF or not?
$\angle A =70^{o}$, $\angle C = 35^{o}$ and $\angle D = 75^{o}$ , $\angle F = 70^{o}$
Solution:
We are given the values of two angles for both triangles, and this data is insufficient for us to tell whether or not these triangles are similar. We need to determine the third angle to determine if these two triangles are similar.
We can see that the $\triangle$ ABC has one angle similar to that of the $\triangle$ DEF. $\angle A = \angle F$. If one more angle is found similar, then by A. A similarity, these two triangles will be called similar triangles.
We know that the total angle of the triangle is $180^{o}$. So, $\angle A + \angle B + \angle C =180^{o}$.
$70^{o}+ \angle B + 35^{o} = 180^{o}$
$105^{o}+ \angle B = 180^{o}$
$\angle B = 180^{o}- 105^{o}$
$\angle B = 75^{o}$.
So we can see that $\angle A = \angle F$ and $\angle B = \angle D$. Hence, by A.A theorem we can write $\triangle$ ABC $\sim \triangle$ DEF.
Example 2
From the given data, determine whether $\triangle$ ABC is similar to $\triangle$ DEF or not ?
$AB = 5cm$, $BC = 10 cm$ and $AC = 12 cm$
$DE = 2.5 cm$, $EF = 5 cm$ and $DF = 6cm$
Solution:
We are given the length of all the sides of the both triangles and now if the corresponding ratios of the sides of triangles are similar then $\triangle$ ABC will be similar to $\triangle$ DEF.
$\dfrac{AB}{DE} = \dfrac{5}{2.5} = 2$
$\dfrac{BC}{EF} = \dfrac{10}{5} = 2$
$\dfrac{AC}{DF} = \dfrac{12}{6} = 2$
As $\dfrac{AB}{DE} = \dfrac{BC}{EF} = \dfrac{AC}{DF}$
So the triangle ABC is similar to triangle DEF the lengths of the sides of triangles were given and the ratio of corresponding sides is equal, hence $\triangle$ ABC $\sim \ \triangle$ DEF.
Example 3
If $\triangle$ ABC is similar to $\triangle$ DEF find the value of x?
$BC = 6cm$, $AC = 5 cm$ and $\angle C = 50^{o}$
$DE = 6cm$, $DF = 5cm$ and $\angle x =$ ?
Solution:
We are given that both triangles are similar, so by the SAS theorem, two sides and one angle should be similar. As both sides of both triangles are similar, the value of x would equal $50^{o}$.
Frequently Asked Question
If $\triangle$ ABC Is Similar to DEF, the Sides of ABC Must Be Congruent to the Corresponding Sides of DEF?
No, it is not necessary that all the sides of $\triangle$ ABC must be congruent to all the sides of $\triangle$ DEF for both the triangles to be called similar triangles. Similar triangles are the same in shape but can vary in size. Two triangles can be called similar even if two corresponding angles of both triangles are similar or if two sides along with one angle are equal.
Here is a quick table to explain this further:
Similar Triangles | Congruent Triangles |
| They have the same shape, but the size of the triangles may be different. Whenever similar triangles are magnified or de-magnified, they will superimpose each other. | Congruent triangles are always similar in shape and size, which means all three sides of the first triangle will be equal to the corresponding sides of the second triangle. Congruent triangles do not magnify or de-magnify when superimposed; they keep the original shape. |
| Similar triangles are represented by the symbol “$\sim$.” For example, if the triangle ABC is similar to the triangle PQR then we will write it as $\triangle$ ABC $\sim \triangle$ PQR | Congruent triangles are represented by the symbol “$\cong$.” For example, if $\triangle$ ABC is congruent to $\triangle$ DEF then we will write it as $\triangle$ ABC $\cong \triangle$ DEF |
| In similar triangles, the ratio of all the corresponding sides of both triangles will be equal to each other. The value of the ratio will depend upon the length measurements of the sides. | If triangles are congruent, the ratio of all the corresponding sides of triangles will always be equal to 1. |
Conclusion
Let us now recap the conditions which are necessary for $\triangle$ ABC to be similar to $\triangle$ DEF.
• If $\triangle$ ABC is similar to $\triangle$ DEF, then they will have the same shape, but the size of both triangles may be different.
• $\triangle$ ABC will be similar to $\triangle$ DEF if any two angles of $\triangle$ ABC are similar to $\triangle$ DEF.
• $\triangle$ ABC will be similar to $\triangle$ DEF if two sides along with their corresponding angle of $\triangle$ ABC is equal to two sides and their corresponding angle of $\triangle$ DEF.
• $\triangle$ ABC will be similar to $\triangle$ DEF if the corresponding ratios of all sides of both triangles are equal to each other.
After reading this guide, you have now hopefully grasped the concept of when $\triangle$ ABC is similar to $\triangle$ DEF. You are now able to solve questions related to similar triangles.
