JUMP TO TOPIC
 The zero slope of a line means that it is horizontal and rises or inclines like a slope.
The zero slope of a line means that it is horizontal and rises or inclines like a slope.
If a line is perfectly horizontal across the Cartesian plane, then the slope of that line will be zero.
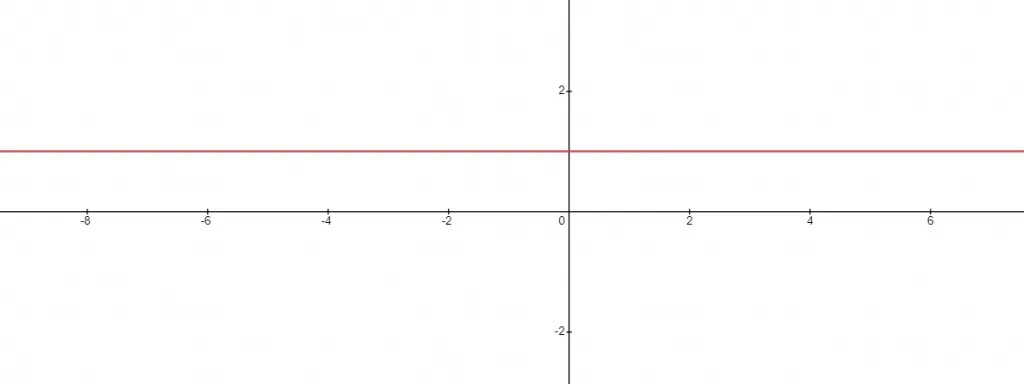
Consider a person riding a bicycle on a plane horizontal road. Then, the slope at any point of the road is always zero.
This guide will help you understand the concept of the slope and its types. We will also discuss how to calculate the slope and in which scenario the slope of a function is considered zero.
What Is Zero Slope?
The zero-slope of a function states that the function is a straight flat line, in short, no matter what the value of the x-coordinate is, the value of the y-coordinate will always be constant. To understand the concept of zero-slope, let us first discuss what is meant by slope itself.
Types of Slope
The slope of the line is the difference between the coordinates of two points, or in simple terms, it is a change in the position of the line between two points on a Cartesian plane. The slope of a line is the rate of change of rising of the line or the steepness of the line. The slope of the line is denoted by “m.”
We can determine the slope by taking the difference between the position of two points on the line. It is the ratio of change in the value of the y-coordinate to change in the value of the x-coordinate. The equation for a line is given as:
$y = mx + c$
Here “m” is the slope of the line. If the equation of the line is given as:
$y = 4x + 6$
The slope of the given line is $4$. As we discussed earlier, a slope is a ratio; for the given equation, we can write it as $\dfrac{4}{1}$. We can see from the equation’s graph also that the line is not horizontal, so this function will have a non-zero slope.
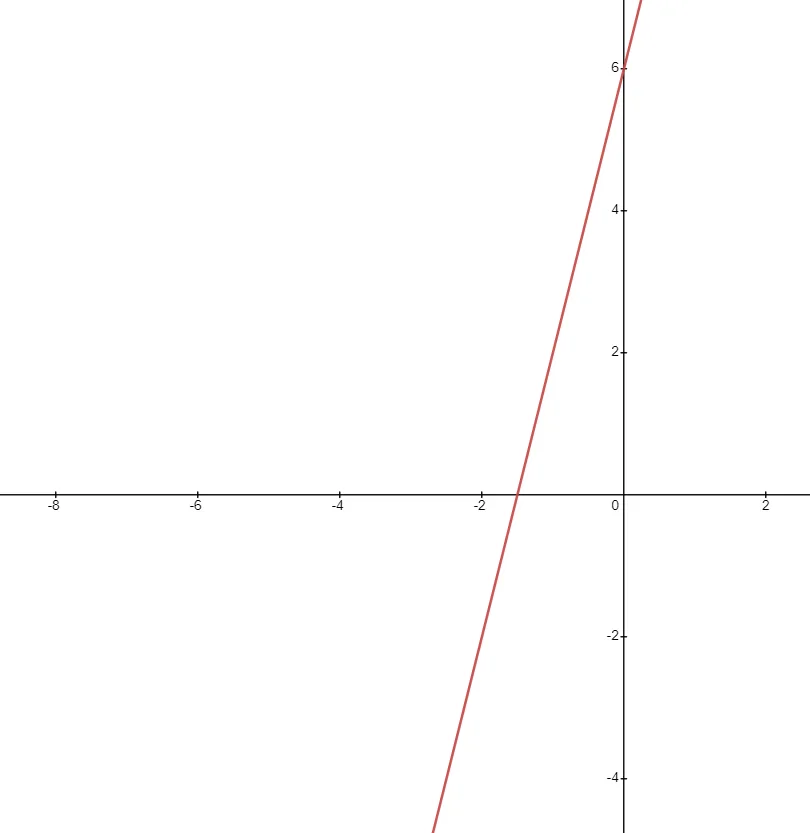
Depending on the slope’s value and direction, we can divide the slope of a line into three different types. A) Positive Slope B) Negative Slope C) Zero Slope
Positive Slope: The slope of the line is said to be positive if an increase along the x-axis accompanies a rise along the y-axis.
Negative Slope: The slope of the line is said to be negative if a rise along the y-axis is accompanied by a decrease along the x-axis and vice versa.
Zero Slope: The slope of a function or a line is zero if no change along the y-axis accompanies a change along the x-axis.
As in mathematics, if we divide a number by zero, the answer will always be zero. Similarly, even if we divide a straight line into smaller parts, the slope of the horizontal line will always be zero since there is no rise in the line at any instance, so it will always appear to be a straight line from left to right. The slope of the said line will always be zero.
Zero Slope and Value of “m”
As discussed earlier, the zero-slope means that the line is horizontal and is parallel to the x-axis in a cartesian plane. The value of “m” for a horizontal line is equal to zero, so for the line having a zero-slope the value of “m” is equal to zero while the angle of the line will be either \theta = $0^{o}$ or $180 ^{o}$.
The rise or change in value of “y” is represented as $\Delta y = y_2 \hspace{1mm} – \hspace{1mm}y_1$ while the rise of change in value of “x” is represented as $\Delta x = x_2\hspace{1mm} – \hspace{1mm}x_1$. For the line having zero slope there is no change in the value of y-coordiantes, which means that $y_2 = y_1$. So, the value of “m”
$m = \dfrac{y_2\hspace{1mm} -\hspace{1mm} y_1}{x_2\hspace{1mm} –\hspace{1mm} x_1}$
$m = \dfrac{0}{ x_2\hspace{1mm} – \hspace{1mm}x_1}$
If we divide zero by any number the answer will always be zero. So , we can say that
$m = \dfrac{rise}{run} = \dfrac{\Delta y}{\Delta x} = 0$
The value of the slope is the rise or fall of the line in the two-dimensional Cartesian plane. The line having zero-slope means the value of the y-coordinates along the y-axis remains unchanged, while the value of x coordinate changes.
The slope of a line is also known as the tangent of the line, so it means calculating the slope of the line using an angle. We put the value of the angle in the tangent to calculate the slope of the line. When the slope of a line is equal to zero, then the value of “m” can be written as:
$m = Tan (0^{o}) \,\, or\,\, Tan (180^{o}) = 0$
The line having a zero-slope is a perfectly horizontal line, as it is a horizontal line. Hence, it intersects the y-axis only at one point since it is cutting the y-axis at one point only, so there is no change in the value of “y” and we can write the point of intersection as (0, b). The point is at a distance of “b” units form x-axis, so the slope of one, two, or the slope of three different points on the horizontal line will be zero as the value of y does not change.
Zero Slope Graph
The graph of the zero-slope can be represented by showing the change in the value of x and y coordinates along the two-dimensional cartesian plane. We know that to plot the graph of a zero slope, the value of y will remain constant while the value of x will change across the x-axis.
Suppose we want to plot the graph between two points represented across the x and y-axis. As we plot a line with zero slope, we will keep the value of y as constant. So the value of the quantity/variable will change across the x-axis, but the value of “y” or secondary quantity will remain the same across the y-axis. This change can be shown in graphical form as:
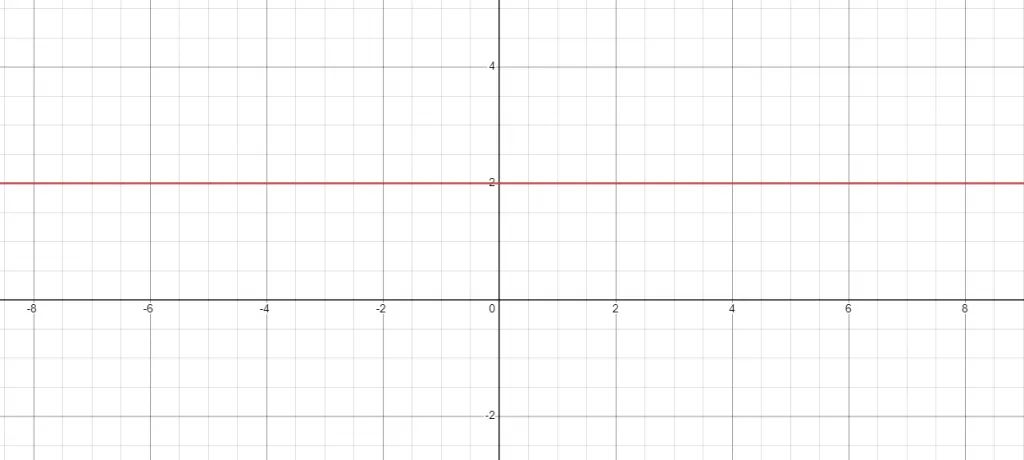
As we can see from the figure above, the line is perfectly horizontal and it is parallel to the x-axis, hence the slope of the line is zero. As it is a horizontal line so the total angle of the line is $0^{o}$ and the value of $tan(0^{o}) = 0$.
How To Calculate the Zero Slope of a Line/Function
The slope of a horizontal line can be calculated by using three different methods, so we can prove that the slope of a horizontal line is zero by using any of these three methods.
1. Distance between two points or rate of change of x and y coordinates
2. Angle of the line along the x-axis
3. Calculating the derivative of the line or curve.
Distance between two points: The distance between the two points on a line is basically the change in the value of x and y coordinates. Let’s assume the two points on the line can be written as $(x_1,y_1)$ and $(x_2, y_2)$ then the slope of the line can be calculated as:
$Slope = \dfrac{y_2\hspace{1mm} –\hspace{1mm} y_1}{x_2\hspace{1mm} – \hspace{1mm}x_1}$
We know that if the slope of the line is zero, then the line will be a horizontal line and we can see from the picture below that no matter which two points we take to calculate the distance between them, the value of the y coordinate will remain the same. Hence, the value of the slope will be zero.
$Slope = \dfrac{y \hspace{1mm}–\hspace{1mm} y}{x_2\hspace{1mm} – \hspace{1mm}x_1}$
$Slope = \dfrac{0}{x_2\hspace{1mm} –\hspace{1mm} x_1} = 0$
The angle of the line: The second method that can be used to determine the slope is by using the angle of the line along the x-axis. As we know, in the case of a horizontal line the angle will either be $0^{o}$ or $180^{o}$. When the angle is taken in a clock-wise direction, it will be taken as $0^{o}$. If the angle is taken in an anti-clockwise direction it will be taken as $180^{o}$. In both cases, the value of the angle is put in the tangent to calculate the value of the slope.
So the slope of a horizontal line can be calculate by using the tangent formula $m = tan(\theta)$, where $\theta$ is either $0^{o}$ or $180^{o}$. $Tan (0^{o}) = Tan (180^{o}) = 0$.
Derivative of the line/curve: The third and final method that can be used to show that the slope of the horizontal line is always zero is by calculating the slope by taking the derivative of the line or linear equations. For a given function f(x) the slope of the curve will be equal to the slope of the tangent at a given point and that can be written as $m = \dfrac{dy}{dx}$. Since we know that there is no change in the value of “y,” hence dy = 0 so the value of m will be equal to zero.
Zero Slope vs Undefined Slope
We know that the line that intercepts the y-axis at only one point will be referred to as a horizontal line and the slope of such a line will always be zero. On the contrary, the line that passes through the x-axis only at one point will be vertical and the slope of such a line is defined as an undefined slope and can be shown as:
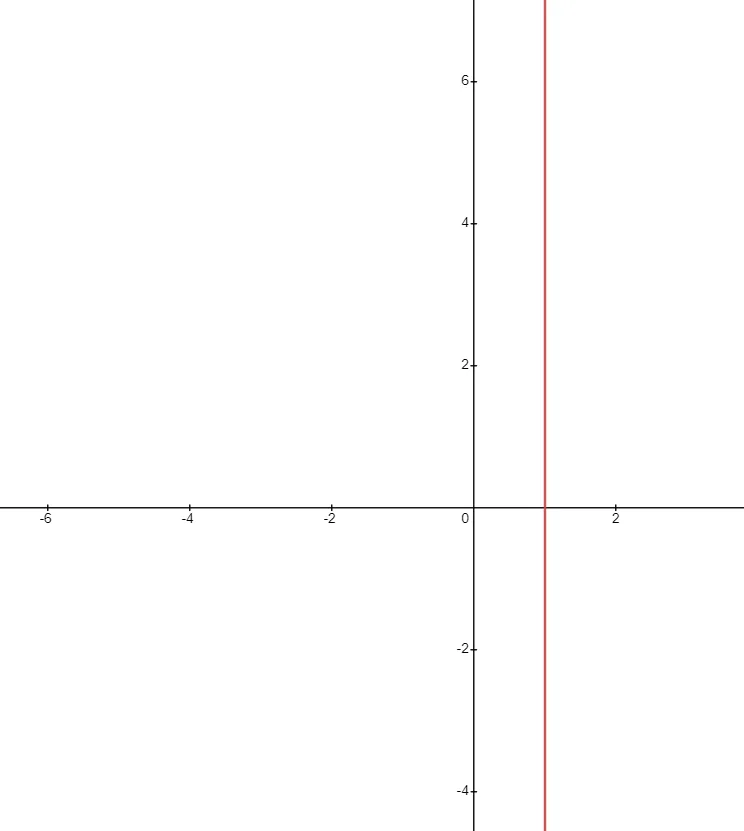
So if we want to explain it in simple terms, we can simply say if the change in the value of y coordinates is zero or if the value of y remains constant for any line, then the line will have zero slope. And if the value of x remains constant at different points on the line while the value of y changes, then such a line will have an infinite or undefined slope.
Example 1: Suppose you are given a line having a slope = 0. You are required to determine the point on the same line that is 6 units away from the point $(4,6)$.
Solution:
The slope of the given line is zero, hence the value of “y” will remain constant. So, any other point on the line will be of the form $(x, 6)$.
We are required to determine the point that is 6 units away from (4,6) as the direction has not mentioned that point can either be $(4 – 6,6)$ or $ 4+6, 6)$.
So, the point can either be $(-2,6)$ or $(10,6)$ for the given line.
Example 2: Determine the point on a horizontal line, the point should be 5 units away from the point $(2,5)$.
Solution:
We are given a horizontal line and we know that the slope of the horizontal line is zero, hence the value of “y” will remain constant. So, any other point on the line will be of the form $(x, 5)$.
We are required to determine the point that is 5 units away from $(2,5)$ as the direction has not mentioned that point can either be $(2 – 5,5)$ or $(2+5, 5)$.
So, the point can either be $(-3, 5)$ or $(7,6)$ for the given line.
Practice Questions:
1. Determine the point on a horizontal line that is 3 units away from the point $(1,7)$.
2. Determine the point on a horizontal line that is 1 unit away from the point $(3,3)$.
Answer Keys:
1).
The point can either be $(4,7)$ or $(-2,7)$.
2).
The point can either be $(2,3)$ or $(4,3)$.
