Equation of a Semicircle – Definition, Properties, and Examples

A semicircle, as the name suggests, is one-half of a circle. While circles have been central to human civilization for millennia, from the wheels of carts to the intricate designs in cathedrals, semicircles too have their unique charm and utility.

Understanding the equation of a semicircle offers a glimpse into a world where mathematics marries art, architecture, and more.

Defining the Equation of a Semicircle

The equation of a semicircle is defined as:

• Upper Semicircle: y = $\sqrt{r^2  –  x^2}$​
• Lower Semicircle: y = – $\sqrt{p^2  –  x^2}$

Depending on its orientation (upper or lower half), a semicircle has an equation governed by the above two equations.

Defining a Semicircle

A semicircle can be defined as the shape that results when you cut a full circle along its diameter. The cut divides the circle into two congruent shapes, each being a semicircle. The defining feature of a semicircle is its diameter, which doubles as its straight edge, unlike a circle, which is defined by its center and radius.

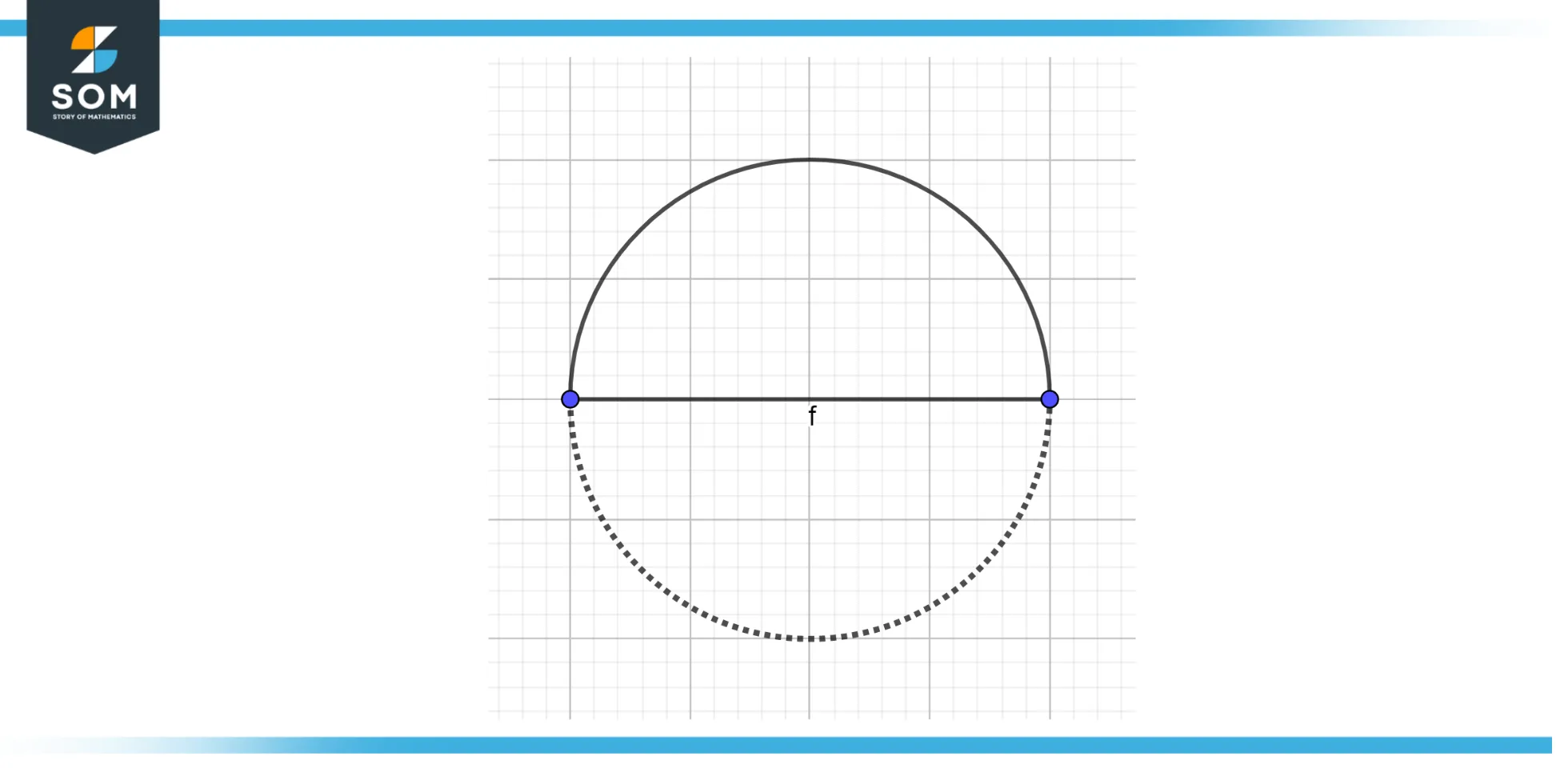
Figure-1.

Mathematical Representation 

The equation of a full circle with a center at the origin (0, 0) of a coordinate plane and a radius $r$ is $x^2$ $+\; \$y^2\$=\; \$r^2\$$. However, a semicircle, depending on its orientation (upper or lower half), has an equation governed by the following:

• Upper Semicircle: y = $\sqrt{r^2  –  x^2}$​
• Lower Semicircle: y = – $\sqrt{p^2  –  x^2}$

If the semicircle’s center is not at the origin and is instead $(h,k)$, then the equation modifies accordingly.

Adjusting the Center

While the standard equation of a semicircle assumes the center is at the origin, in many cases, it’s not. Let’s say the center of our semicircle is at $(h,k)$. The equation for the upper half becomes:

y − k = $x^2$ − $\sqrt{x-h}$

For the lower half, it is:

y − k = – $r^2$ − $\sqrt{x-h}$​

Exercise 

Example 1

Find the equation of the upper semicircle with radius 4 units and centered at the origin.

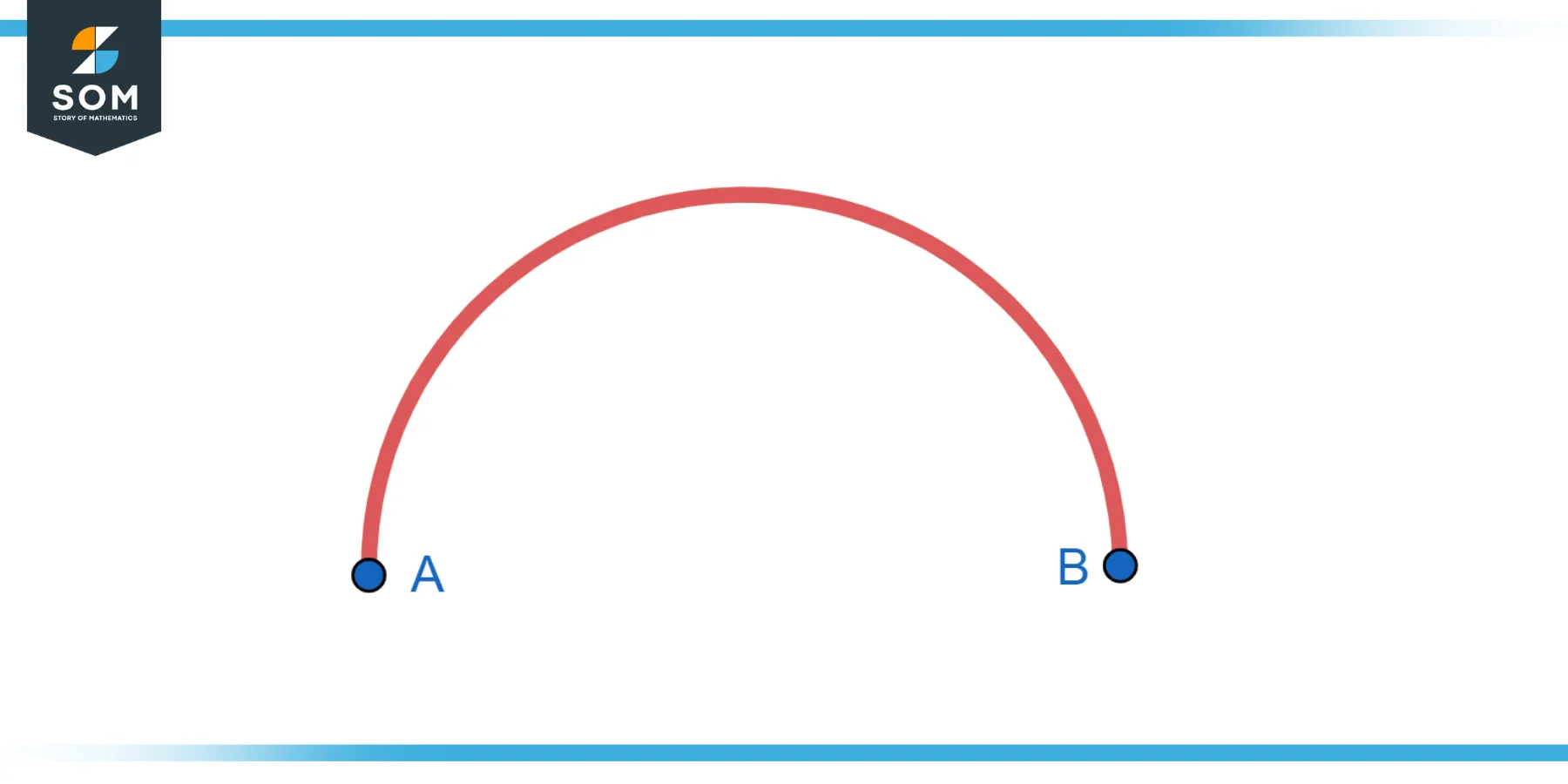
Figure-2.

Solution

Equation of the circle:

$x^2$ $+\; \$y^2\$=16$

For the upper semicircle:

y = $\sqrt{16  –  x^2}$​

Example 2

Find the equation of the lower semicircle with a radius of 3 units centered at the origin.

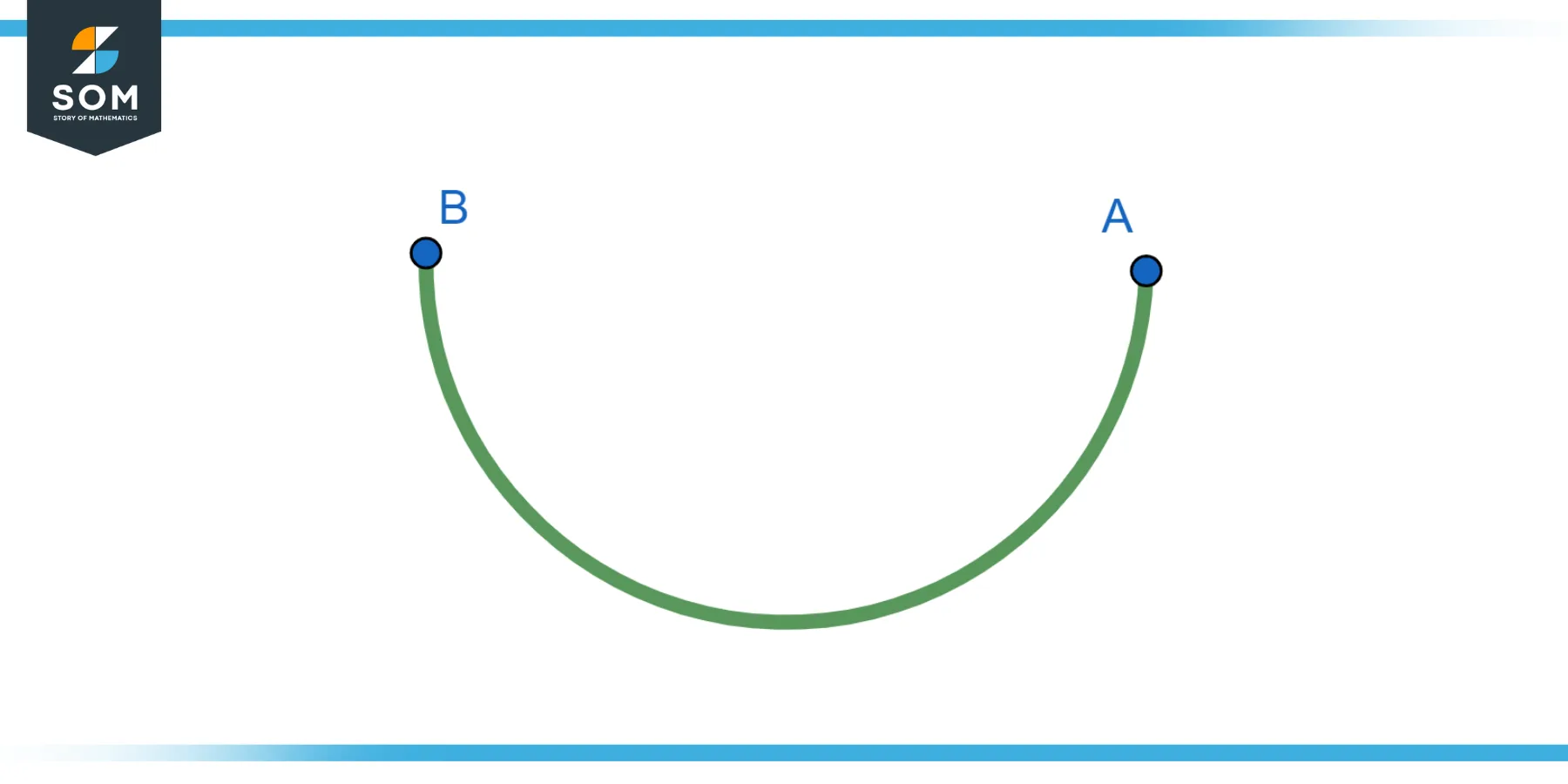
Figure-3.

Solution

Equation of the circle:

$x^2$ $+\; \$y^2\$=\; 9$

For the lower semicircle:

y = – $\sqrt{9  –  x^2}$​

Example 3

Determine the equation of the upper semicircle with radius 5 and centered at (2, 3).

Solution

Equation of the circle:

${(x-2)^2  –  (y – 3)^2}$ = 25

For the upper semicircle:

y = 3 + $\sqrt{25  –  (x-2)^2}$

Applications of the Equation of a Semicircle in Different Fields

• Architecture & Construction

  • Arches: One of the most iconic applications of semicircles in architecture is the semicircular arch, prevalent in Roman and Gothic architectural designs. These arches are not only aesthetically pleasing but also distribute weight efficiently, making structures more stable.
  • Domes: Semi-domes, which are essentially 3D adaptations of semicircles, are often found in religious and monumental architecture. Their shape provides both structural stability and acoustic benefits.
  • Design Elements: Semicircular patios, terraces, and balconies are popular in modern designs, offering unique vistas and efficient use of space.

• Art & Design

  • Patterns and Motifs: Semicircular patterns are popular in various art forms, from mosaics to fabric designs, offering symmetrical aesthetics.
  • Sculptures: Many sculptures, especially fountains and monuments, utilize semicircular designs for visual balance and focus.

• Engineering

  • Bridges: Some bridges employ semicircular designs for their arches, distributing the forces of tension and compression efficiently.
  • Tunnels: The cross-sectional design of many tunnels is semicircular, which helps in optimizing structural integrity against the forces of the earth.

• Mathematics & Physics

  • Trigonometry: The unit circle’s representation in trigonometry often involves using semicircles to explain sine, cosine, and their relationships.
  • Optics: The principle of reflection in concave mirrors (which are semicircular in shape) is based on the equation of the semicircle.

• Nature & Environment

  • Landscaping: Gardens and parks sometimes employ semicircular designs for aesthetic appeal, especially in water features or seating arrangements.
  • Environmental Studies: The study of phenomena like rainbows and horizons, which can often appear semicircular, involves understanding the properties of this shape.

• Sports

  • Tracks: Many athletic tracks have semicircular ends, and understanding the curvature helps in designing the lanes.
  • Fields: Certain sports, like basketball, involve semicircular regions (e.g., the three-point arc).

• Technology & Electronics

  • Communication: Satellite dishes, which are often semicircular, utilize the shape’s properties to capture signals effectively.
  • Device Design: Many gadgets and electronics, from headphones to certain screen designs, employ semicircular aesthetics and functionality.

• Medicine

  • Medical Imaging: Devices like MRIs have a semicircular design, allowing the patient to be at the center of the imaging device for optimal results.
  • Prosthetics: Some prosthetic designs, especially for joints, may use semicircular components to mimic the natural curvature of the body.

Challenges & Complexities

While the semicircle’s equation might appear straightforward, many complexities arise when:

Intersecting with Other Shapes

The point of intersection of a semicircle with other geometric figures can result in complicated equations.

Transformation

Translating, rotating, or performing other transformations on a semicircle can introduce complexities in the mathematical representation.

Real-World Imperfections

When transitioning from paper to reality, imperfections, and challenges, like material constraints or environmental factors, can influence the ideal semicircular shape.

All images were created with GeoGebra.