JUMP TO TOPIC

We explore the geometric series test, a cornerstone concept in mathematical sequences and series. This article will delve into the theory, proofs, and applications of this influential test.
The geometric series test offers a gateway to understanding whether an infinite geometric series converges or diverges, providing a solid foundation for subsequent mathematical theories.
Whether you’re a seasoned mathematician, a budding student, or a curious reader, this exploration will illuminate new facets of mathematics, emphasizing its elegance, rigor, and practical relevance. Join us as we navigate the nuances of this fascinating topic, shedding light on its intriguing implications and potential applications.
Definition of Geometric Series Test
The geometric series test is a mathematical method to determine whether a given geometric series converges or diverges. A geometric series is a sequence of terms in which each subsequent term after the first is found by multiplying the previous term by a fixed, non-zero number called the common ratio.
The test states that a geometric series ∑$r^n$ (where n runs from 0, 1, 2, up to ∞) will converge if the absolute value of r is less than 1 (|r| < 1) and will diverge otherwise. When it converges, the sum of the geometric series can be found using the formula S = a / (1 – r), where ‘a’ is the first term and ‘r’ is the common ratio.
Below we present a generic representation of the geometric series in continuous and discrete form in figure-1.
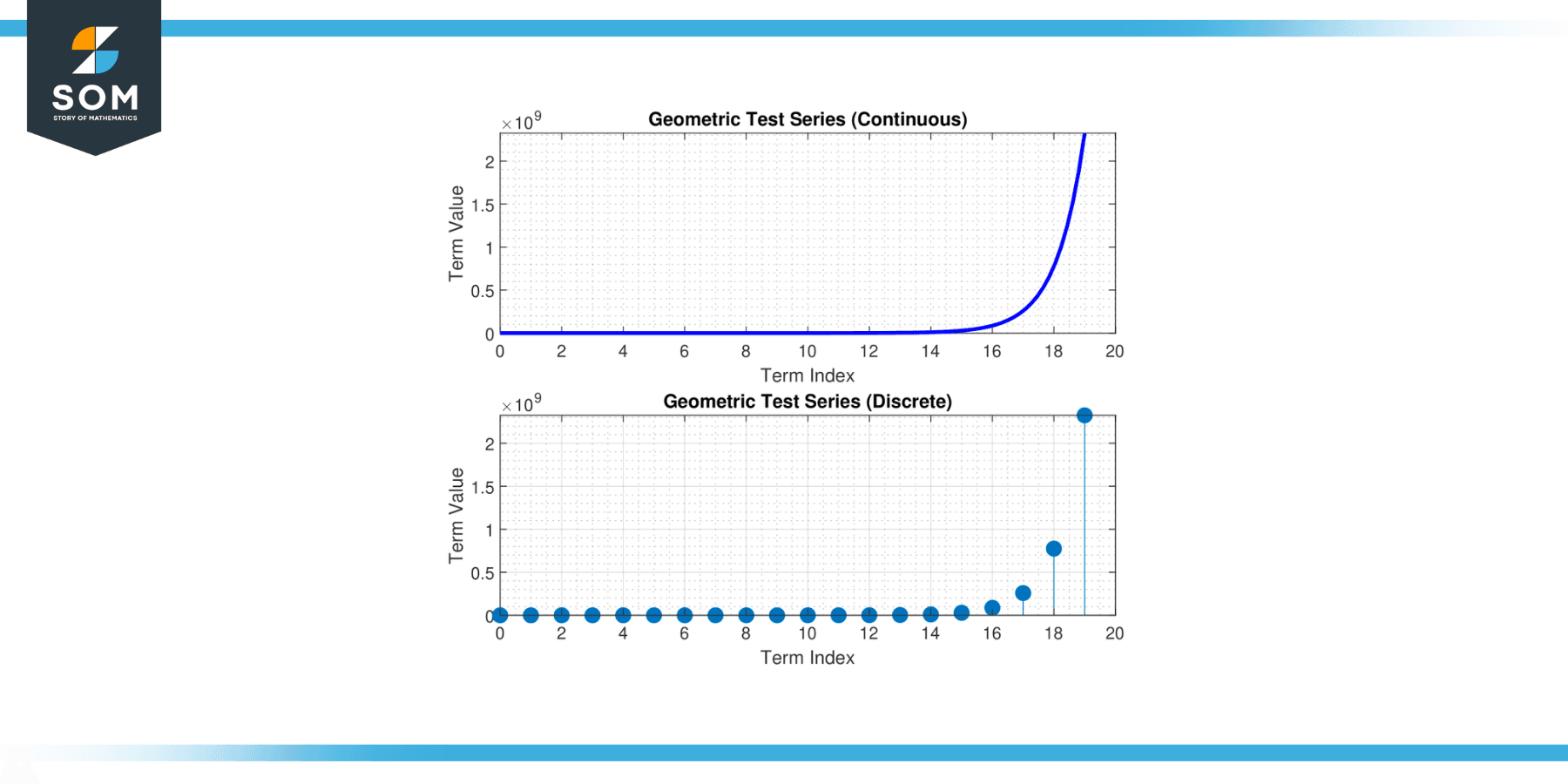
Figure-1.
Historical Significance
The concept of geometric series has been known since ancient times, with early evidence of its use found in both Greek and Indian mathematics.
The ancient Greeks were among the first to explore geometric series. The philosopher Zeno of Elea, famous for his paradoxes, devised a series of thought experiments that implicitly relied on geometric series, particularly his “dichotomy paradox,” which essentially describes a geometric series where the common ratio is 1/2.
Indian mathematicians, notably in the classical age around 5th to 12th century AD, made substantial contributions to the understanding of geometric progressions and series. A key figure in this development was Aryabhata, an Indian mathematician and astronomer from the late 5th and early 6th century, which used geometric series to give a formula for the sum of finite geometric series and applied it to compute interest.
The understanding of the geometric series evolved significantly in the late Middle Ages, particularly with the work of medieval Islamic mathematicians. They used geometric series to solve algebraic problems and offered explicit formulas for the sum of finite geometric series.
However, it wasn’t until the 17th century and the advent of calculus that mathematicians studied the convergence and divergence of infinite series more systematically. The understanding of geometric series, including the convergence criterion (|r| < 1 for convergence), was deepened with the work of mathematicians like Isaac Newton and Gottfried Wilhelm Leibniz, the co-founders of calculus.
The geometric series test, as it is understood today, is essentially the culmination of centuries of accumulated knowledge, stretching back to the ancient Greeks and Indians, through the Islamic mathematicians of the Middle Ages, up to the mathematical pioneers of the Age of Enlightenment. Today, it remains a fundamental concept in mathematics, underpinning many areas of study and application.
Properties
Convergence Criterion
The geometric series test states that the geometric series, ∑a*$r^n$ converges if and only if the absolute value of the common ratio is less than 1 (|r| < 1). If |r| >= 1, the series does not converge (i.e., it diverges).
Sum of Converging Geometric Series
If the geometric series converges, its sum can be calculated using the formula S = a / (1 – r), where ‘S’ represents the sum of the series, ‘a’ is the first term, and ‘r’ is the common ratio.
The behavior of the Series
For |r| < 1, as n approaches infinity, the terms in the series approach zero, meaning the series “settles” to a finite number. If |r| >= 1, the terms in the series do not approach zero, and the series diverges, meaning it doesn’t settle for a finite value.
Negative Common Ratio
If the common ratio ‘r’ is negative and its absolute value is less than 1 (i.e., -1 < r < 0), the series still converges. However, the terms of the series will oscillate between positive and negative values.
Independent of First Term
The convergence or divergence of a geometric series does not depend on the value of the first term ‘a’. Regardless of the value of ‘a’, if |r| < 1, the series will converge, and if |r| >= 1, it will diverge.
Partial Sums: The partial sums of a geometric series form a geometric sequence themselves. The n-th partial sum of the series is given by the formula $S_n$ = a * (1 – $r^n$) / (1 – r) for r ≠ 1.
Applications
The geometric series test and the principles of geometric series find applications across a broad range of fields, from pure mathematics to physics, economics, computer science, and even in biological modeling.
Mathematics
The concept of geometric series is instrumental in calculus and is frequently used in conjunction with power series or Taylor series. They can also be used to solve difference equations, which have applications in dynamic systems, like population modeling, where the change in population from year to year follows a geometric pattern.
Physics
In electrical engineering, the principles of geometric series can be used to calculate the equivalent resistance of an infinite number of resistors arranged in parallel or in series. In optics, geometric series can be used to analyze the behavior of light as it repeatedly reflects between two parallel mirrors.
Computer Science
Concepts from geometric series are often found in the design and analysis of algorithms, especially those with recursive elements. For example, binary search algorithms, divide and conquer algorithms, and algorithms dealing with data structures like binary trees often involve geometric series in their time complexity analysis.
Economics and Finance
Geometric series find extensive use in calculating the present and future values of annuities (fixed sum paid every year). They’re also used in models of economic growth and the study of functions of compounded interest. Furthermore, they’re utilized to evaluate perpetuities (an infinite sequence of cash flows).
Biology
Geometric series can be used in biological modeling. In population modeling, for instance, the size of each generation might be modeled as a geometric series, assuming each generation is a fixed multiple of the size of the previous one.
Engineering
In control theory, geometric series can be used to analyze systems’ responses to certain inputs. If a system’s output at any given time is a proportion of its input at the previous time, the total response over time forms a geometric series.
Probability Theory and Statistics
In a geometric distribution, the number of trials needed to get the first success in a series of Bernoulli trials is modeled. Here, the expected value and variance of a geometric distribution are derived using geometric series.
Exercise
Example 1
Determine if the series ∑$(2/3)^n$ from n=0 to ∞ converges or diverges.
Solution
In the series ∑$(2/3)^n$, the common ratio r = 2/3. Since the absolute value of r, |r| = |2/3| = 2/3, which is less than 1, the geometric series converges according to the geometric series test.
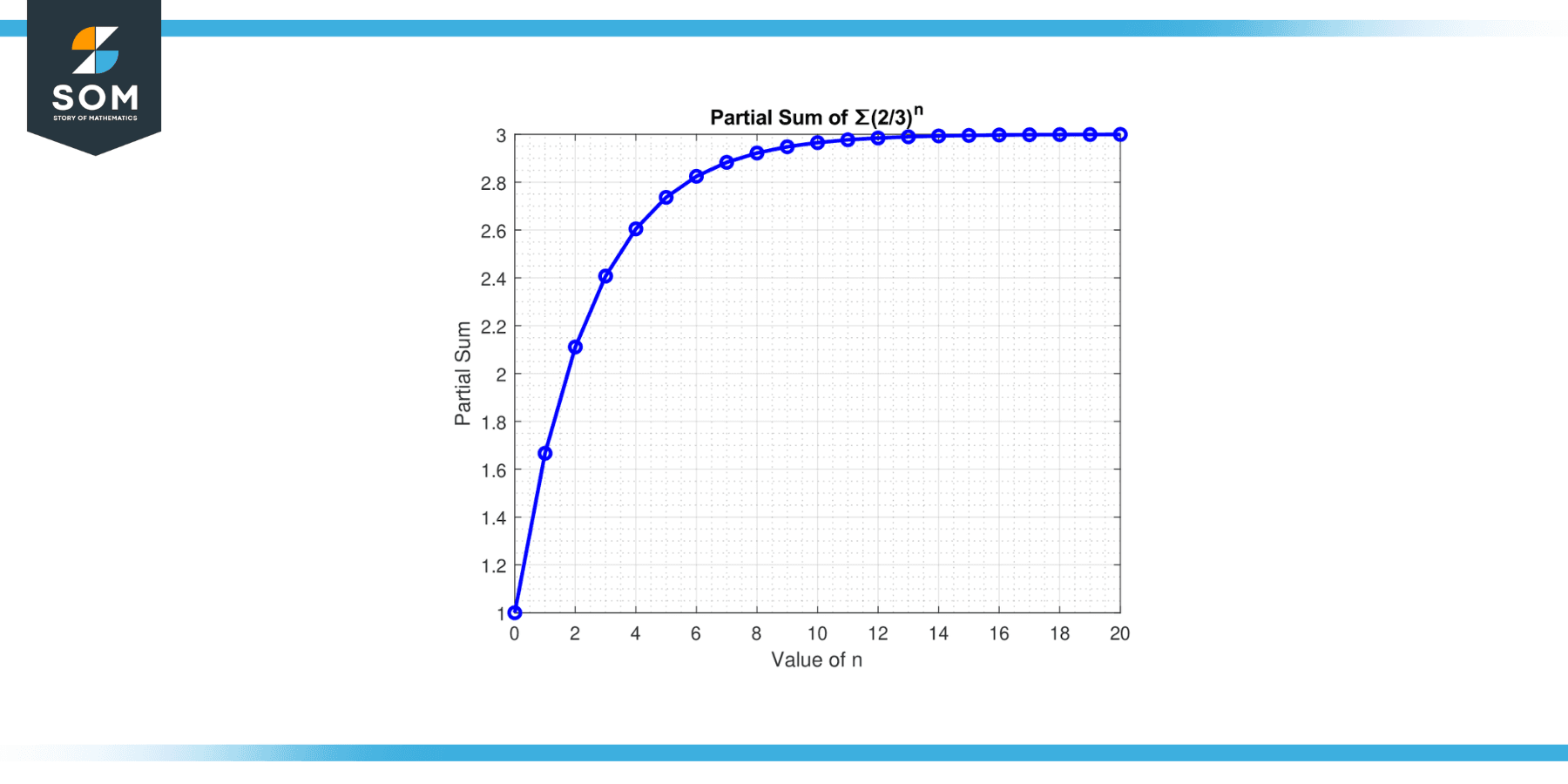
Figure-2.
Example 2
Determine the sum of the series ∑$(2/3)^n$ from n=0 to ∞.
Solution
Since the series ∑$(2/3)^n$ converges, we can find the sum of the series using the formula a / (1 – r), where ‘a’ is the first term and ‘r’ is the common ratio. Here, a = $(2/3)^0$ = 1, and r = 2/3. So, the sum is:
S = 1 / (1 – 2/3)
S = 1 / (1/3)
S = 3
Example 3
Determine if the series ∑$2^n$ from n=0 to ∞ converges or diverges.
Solution
In the series ∑$2^n$, the common ratio r = 2. Since the absolute value of r:
|r| = |2| = 2
which is greater than 1, the geometric series diverges according to the geometric series test.
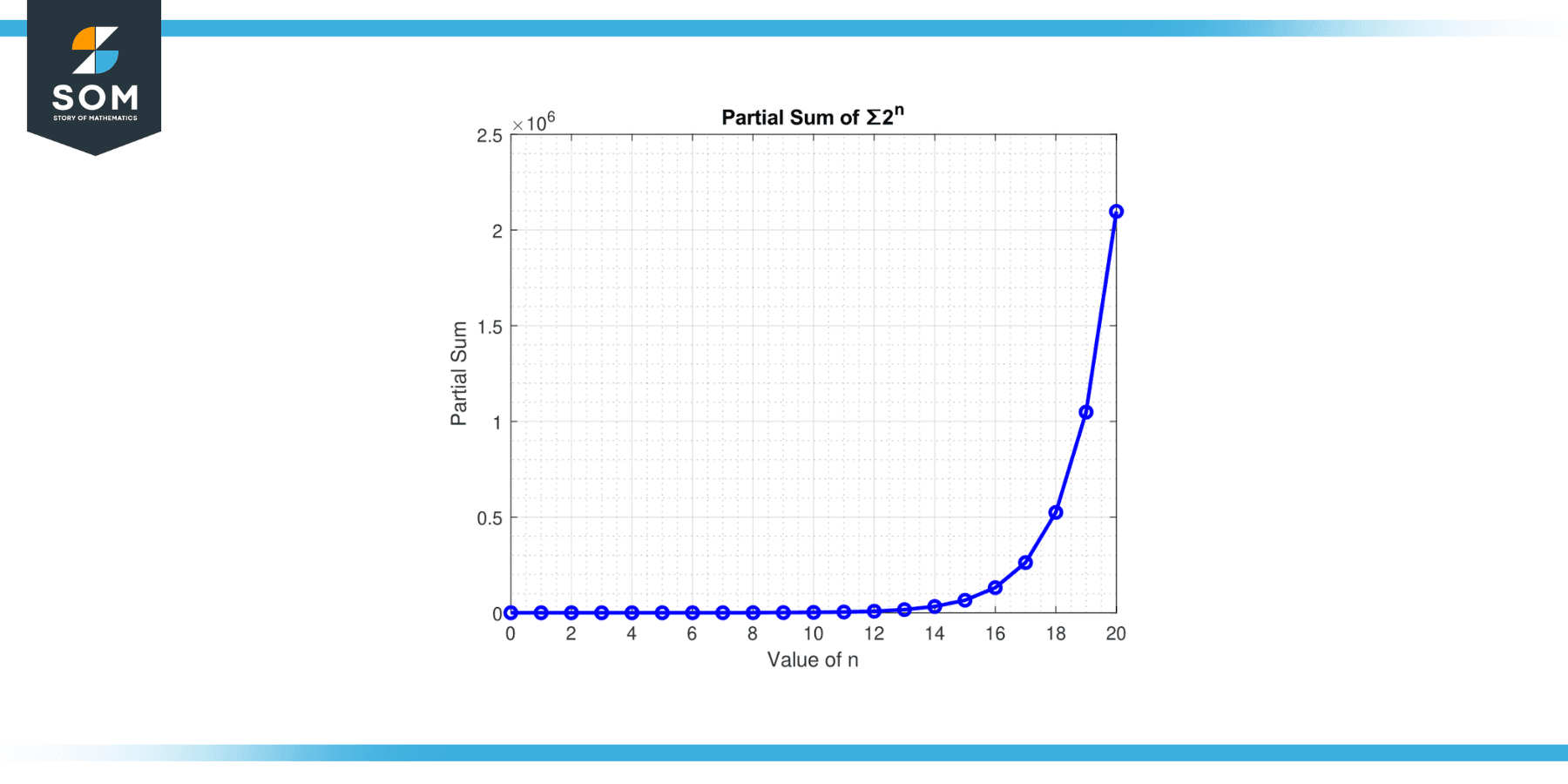
Figure-3.
Example 4
Determine the sum of the series ∑$(-1/2)^n$ from n=0 to ∞.
Solution
In the series ∑$(-1/2)^n$, the common ratio r = -1/2. Since the absolute value of r, |r| = |-1/2| = 1/2, which is less than 1, the geometric series converges according to the geometric series test.
Here:
a = $(-1/2)^0$
a = 1
and
r = -1/2
So, the sum is:
S = 1 / (1 – (-1/2))
S = 1 / (1.5)
S = 2/3
Example 5
Determine if the series ∑$(-2)^n$ from n=0 to ∞ converges or diverges.
Solution
In the series ∑$(-2)^n$, the common ratio r = -2. Since the absolute value of r, |r| = |-2| = 2, which is greater than 1, the geometric series diverges according to the geometric series test.
Example 6
Determine the sum of the series ∑$0.5^n$ from n=1 to ∞.
Solution
In the series ∑$0.5^n$, the common ratio r = 0.5. Since the absolute value of r, |r| = |0.5| = 0.5, which is less than 1, the geometric series converges according to the geometric series test. Here:
a = $0.5^1$
a = 0.5
and
r = 0.5
So, the sum is:
S = 0.5 / (1 – 0.5)
S = 0.5 / 0.5
S = 1
Example 7
Determine if the series ∑$(5/4)^n$ from n=1 to ∞ converges or diverges.
Solution
To determine if the series ∑$(5/4)^n$ from n=1 to ∞ converges or diverges, we need to examine the behavior of the common ratio.
The series can be written as:
∑$(5/4)^n$ = $(5/4)^1$ + $(5/4)^2$ + $(5/4)^3$ + …
The common ratio, denoted by r, is the ratio of consecutive terms. In this case, r = 5/4.
If the absolute value of the common ratio |r| is less than 1, the series converges. If |r| is greater than or equal to 1, the series diverges.
In this example, |5/4| = 5/4 = 1.25, which is greater than 1. Therefore, the series diverges.
The series ∑$(5/4)^n$ from n=1 to ∞ diverges.
Example 8
Determine the sum of the series ∑$(-1/3)^n$ from n=0 to ∞.
Solution
To determine the sum of the series ∑$(-1/3)^n$ from n=0 to ∞, we can use the formula for the sum of a convergent geometric series.
The series can be written as:
∑$(-1/3)^n$ = $(-1/3)^0$ + $(-1/3)^1$ + $(-1/3)^2$ + …
The common ratio, denoted by r, is the ratio of consecutive terms. In this case, r = -1/3.
If the absolute value of the common ratio |r| is less than 1, the series converges. If |r| is greater than or equal to 1, the series diverges.
In this example, |(-1/3)| = 1/3, which is less than 1, therefore, the series converges.
The sum of the series can be calculated using the formula:
a / (1 – r)
where a is the first term and r is the common ratio.
In this case:
a = $(-1/3)^0$
a = 1
and
r = -1/3
The sum is given by:
S = a / (1 – r)
S = 1 / (1 – (-1/3))
S = 1 / (1 + 1/3)
S = 1 / (4/3)
S = 3/4
S ≈ 0.75
Therefore, the sum of the series ∑$(-1/3)^n$ from n=0 to ∞ is approximately 0.75.
All images were created with MATLAB.
