The main objective of this question is to find the three angles of a triangle given three vertices. The angles can be found using the dot product of the vectors representing the sides of the triangle.A triangle is a polygon with three-sides that is also referred to as a trigon. Every triangle possesses $3$ sides and $3$ angles, which may or may not be the same. Triangles are classified as acute, equilateral, isosceles, obtuse, isosceles right, and right triangle.A triangle is formed geometrically by the intersection of three line segments. In each triangle, every side has $2$ endpoints, and the endpoints of all three sides may intersect at three different points in a plane to form a triangle. The three intersecting points are referred to as triangle vertices. The angles inside a triangle are referred to as the interior angles and the sum of three angles of the triangle is always equal to $180^\circ$. Any triangle that is not a right triangle is defined as an oblique triangle.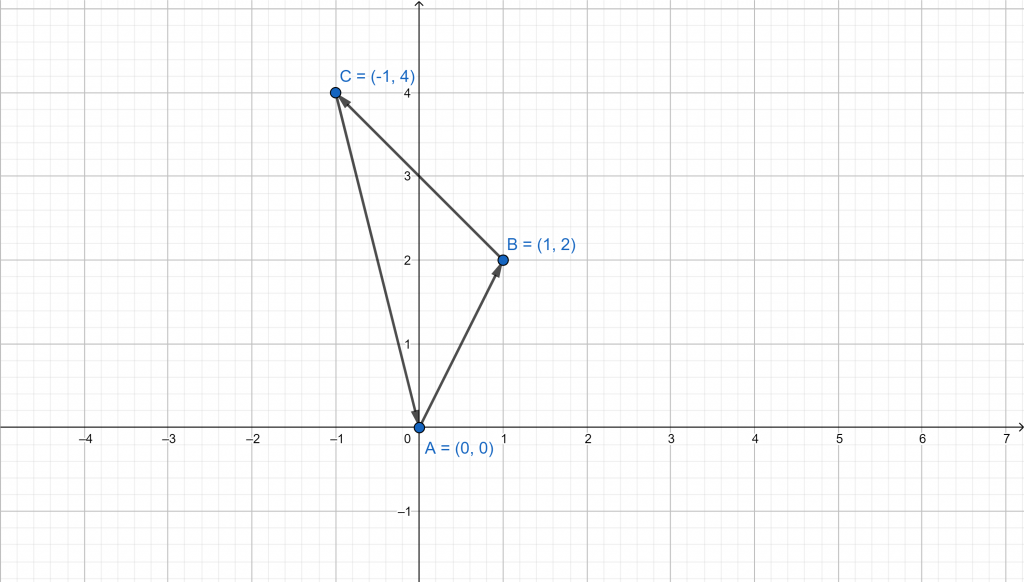
First, find the vectors representing the sides of the triangle.$\overrightarrow{ab}=\langle 1-0,2-0\rangle$ $=\langle 1,2\rangle$$\overrightarrow{ca}=\langle -1-0, 4-0\rangle$ $=\langle -1,4\rangle$$\overrightarrow{bc}=\langle -1-1, 4-2\rangle$ $=\langle -2,2\rangle$The magnitudes of the sides of triangle are:$|\overrightarrow{ab}|=\sqrt{(1)^2+(2)^2}$ $=\sqrt{5}$$|\overrightarrow{ca}|=\sqrt{(-1)^2+(4)^2}$ $=\sqrt{17}$$|\overrightarrow{bc}|=\sqrt{(-2)^2+(2)^2}$ $=2\sqrt{2}$Let $\alpha$ be the angle between $\overrightarrow{ab}$ and $\overrightarrow{ca}$, then by using the dot product:$\cos \alpha=\dfrac{\overrightarrow{ab}\cdot\overrightarrow{ca}}{|\overrightarrow{ab}||\overrightarrow{ca}|}$$\cos \alpha=\dfrac{(1)(-1)+(4)(2)}{(\sqrt{5})(\sqrt{17})}$$\cos \alpha=\dfrac{-1-8}{\sqrt{85}}=$ $-\dfrac{9}{\sqrt{85}}$$\alpha=\cos^{-1}\left(-\dfrac{9}{\sqrt{85}}\right)$$\alpha=12.53^\circ$Let $\beta$ be the angle between $\overrightarrow{ab}$ and $\overrightarrow{bc}$, then by using the dot product:$\cos \beta=\dfrac{\overrightarrow{ab}\cdot\overrightarrow{bc}}{|\overrightarrow{ab}||\overrightarrow{bc}|}$$\cos \beta=\dfrac{(1)(-2)+(2)(2)}{(\sqrt{5})(\sqrt{2})}$$\cos \beta=\dfrac{-2+4}{\sqrt{10}}=$ $\dfrac{2}{\sqrt{10}}$$\beta=\cos^{-1}\left(\dfrac{2}{\sqrt{10}}\right)$$\beta=50.77^\circ$Let $\gamma$ be the angle between $\overrightarrow{ca}$ and $\overrightarrow{bc}$. Since the sum of the angles of a triangle is $180^\circ$, so:$\alpha+\beta+\gamma=180^\circ$$12.53^\circ+50.77^\circ+\gamma=180^\circ$$63.3^\circ+\gamma=180^\circ$$\gamma=180^\circ-63.3^\circ$$\gamma=116.7^\circ$ Images/mathematical drawings are created with GeoGebra.
Expert Answer
Given vertices are:$A(1, 0, -1), B(3, -2, 0), C(1, 3, 3)$First, find the vectors representing the sides of the triangle.$\overrightarrow{AB}=\langle 3-1,-2-0,0+1\rangle$ $=\langle 2,-2,1\rangle$$\overrightarrow{AC}=\langle 1-1, 3-0,3+1\rangle$ $=\langle 0,3,4\rangle$$\overrightarrow{BC}=\langle 1-3, 3+2,3-0\rangle$ $=\langle -2,5,3\rangle$The magnitudes of the sides of triangle are:$|\overrightarrow{AB}|=\sqrt{(2)^2+(-2)^2+(1)^2}$ $=3$$|\overrightarrow{AC}|=\sqrt{(0)^2+(3)^2+(4)^2}$ $=5$$|\overrightarrow{BC}|=\sqrt{(-2)^2+(5)^2+(3)^2}$ $=\sqrt{38}$Let $\alpha$ be the angle between $\overrightarrow{AB}$ and $\overrightarrow{AC}$, then by using the dot product:$\cos \alpha=\dfrac{\overrightarrow{AB}\cdot\overrightarrow{AC}}{|\overrightarrow{AB}||\overrightarrow{AC}|}$$\cos \alpha=\dfrac{(2)(0)+(-2)(2)+(1)(4)}{(3)(5)}$$\cos \alpha=\dfrac{0-4+4}{15}=$ $-\dfrac{2}{15}$$\alpha=\cos^{-1}\left(-\dfrac{2}{15}\right)$$\alpha=97.67^\circ$Let $\beta$ be the angle between $\overrightarrow{AB}$ and $\overrightarrow{BC}$, then by using the dot product:$\cos \beta=\dfrac{\overrightarrow{AB}\cdot\overrightarrow{BC}}{|\overrightarrow{AB}||\overrightarrow{BC}|}$$\cos \beta=\dfrac{(2)(-2)+(-2)(5)+(1)(3)}{(3)(\sqrt{38})}$$\cos \beta=\dfrac{-4-10+3}{3\sqrt{38}}=$ $-\dfrac{11}{3\sqrt{38}}$$\beta=\cos^{-1}\left(-\dfrac{11}{3\sqrt{38}}\right)$$\beta=126.5^\circ$This is the angle outside the triangle because the direction $\overrightarrow{BC}$ is pointing relative to $\overrightarrow{AB}$, and so, we should find the supplementary angle that is:$\beta=180^\circ-126.5^\circ$ $=53.5^\circ$Let $\gamma$ be the angle between $\overrightarrow{AC}$ and $\overrightarrow{BC}$. Since the sum of the angles of a triangle is $180^\circ$, so:$\alpha+\beta+\gamma=180^\circ$$97.67^\circ+53.5^\circ+\gamma=180^\circ$$151.17^\circ+\gamma=180^\circ$$\gamma=180^\circ-151.17^\circ$$\gamma=28.83^\circ$Example
Given the vertices $a(0,0),b(1,2),c(-1,4)$, solve for the three angles of a triangle.Solution
Given vertices are:$a(0,0),b(1,2),c(-1,4)$First, find the vectors representing the sides of the triangle.$\overrightarrow{ab}=\langle 1-0,2-0\rangle$ $=\langle 1,2\rangle$$\overrightarrow{ca}=\langle -1-0, 4-0\rangle$ $=\langle -1,4\rangle$$\overrightarrow{bc}=\langle -1-1, 4-2\rangle$ $=\langle -2,2\rangle$The magnitudes of the sides of triangle are:$|\overrightarrow{ab}|=\sqrt{(1)^2+(2)^2}$ $=\sqrt{5}$$|\overrightarrow{ca}|=\sqrt{(-1)^2+(4)^2}$ $=\sqrt{17}$$|\overrightarrow{bc}|=\sqrt{(-2)^2+(2)^2}$ $=2\sqrt{2}$Let $\alpha$ be the angle between $\overrightarrow{ab}$ and $\overrightarrow{ca}$, then by using the dot product:$\cos \alpha=\dfrac{\overrightarrow{ab}\cdot\overrightarrow{ca}}{|\overrightarrow{ab}||\overrightarrow{ca}|}$$\cos \alpha=\dfrac{(1)(-1)+(4)(2)}{(\sqrt{5})(\sqrt{17})}$$\cos \alpha=\dfrac{-1-8}{\sqrt{85}}=$ $-\dfrac{9}{\sqrt{85}}$$\alpha=\cos^{-1}\left(-\dfrac{9}{\sqrt{85}}\right)$$\alpha=12.53^\circ$Let $\beta$ be the angle between $\overrightarrow{ab}$ and $\overrightarrow{bc}$, then by using the dot product:$\cos \beta=\dfrac{\overrightarrow{ab}\cdot\overrightarrow{bc}}{|\overrightarrow{ab}||\overrightarrow{bc}|}$$\cos \beta=\dfrac{(1)(-2)+(2)(2)}{(\sqrt{5})(\sqrt{2})}$$\cos \beta=\dfrac{-2+4}{\sqrt{10}}=$ $\dfrac{2}{\sqrt{10}}$$\beta=\cos^{-1}\left(\dfrac{2}{\sqrt{10}}\right)$$\beta=50.77^\circ$Let $\gamma$ be the angle between $\overrightarrow{ca}$ and $\overrightarrow{bc}$. Since the sum of the angles of a triangle is $180^\circ$, so:$\alpha+\beta+\gamma=180^\circ$$12.53^\circ+50.77^\circ+\gamma=180^\circ$$63.3^\circ+\gamma=180^\circ$$\gamma=180^\circ-63.3^\circ$$\gamma=116.7^\circ$ Images/mathematical drawings are created with GeoGebra.