
This article aims to find the volume of the solid formed by rotating the shaded region about the y-axis. The article uses the concept of volume of the solid. The volume of the solid generated by a region under $f(x)$ bounded by the y-axis and vertical lines $ y=a $ and $ y=b $, which is revolved about the y-axis, is:
\[V = \int A dx\]
Where:
\[A = \pi r ^ { 2 } \: and \: r = f(x) \]
\[V = \pi \int_{ a } ^ { b } x ^ { 2 } dy \]
Volume
Area of surface

Shade of solid
Expert Answer
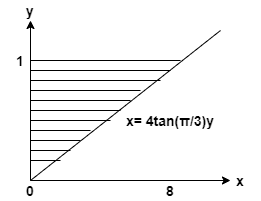
The given curve is:
\[ y = 1, x= 0 , x = 4 \tan(\dfrac { \pi } { 3 } ) y \]
Find the volume of solid formed by rotating the shaded region about the y-axis.
\[ V = \int_{ 0 } ^ { 1 } \pi (4 \tan(\dfrac{\pi}{3})y) ^ { 2 } dy \]
\[= 16 \int_{0}^{1} \tan ^ { 2 } (\dfrac{ \pi } { 3 } y) dy \]
Let:
\[\dfrac{\pi}{3}y = z , \dfrac{\pi}{3}dy \Rightarrow = dz \]
\[y=0 \Rightarrow z= 0\: and \: y =1 \Rightarrow z = \dfrac{\pi}{3} \]
\[V = 16\pi \int_{0} ^ { \dfrac { \pi } { 3 } } \tan ^ { 2 } z ( \dfrac { 3 }{ \pi } ) dz = 48 \int_{ 0 } ^ { \ dfrac { \pi } { 3 } } \tan ^ { 2 } z \: dz \]
Since:
\[\sec ^ { 2 } x – \tan ^ { 2 } x = 1\]
\[=48 \int_{0} ^ { \dfrac { \pi}{3}} \sec^{2} z \: dz \:- 48\: \int_{0}^{\dfrac{\pi}{3}} 1 \:dz\]
\[ = 48 \tan z | _{ 0 } ^{ \dfrac { \pi } { 3 } } – \: 48 z |_{0} ^ { \dfrac { \pi }{3}}\]
\[= 48 ( \tan (\dfrac{ \pi } { 3 }) – \tan 0) – \:48(\dfrac{ \pi }{ 3 } – 0) \]
\[ = 48 (\sqrt { 3 } -0) – 48 \dfrac{ \pi } { 3 } \]
\[= 48(\sqrt { 3 } – \dfrac{ \pi } { 3 })\]
The volume of solid generated by revolving the shaded region is $ 48(\sqrt {3} – \dfrac{\pi}{3})$.
Numerical Result
The volume of solid generated by revolving the shaded region is $ 48(\sqrt {3} – \dfrac{\pi}{3})$.
Example
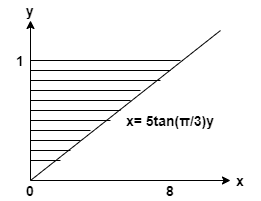
Find the volume of solid generated by revolving the shaded region about the y-axis.
Solution
The given curve is:
\[ y = 1, x= 0 , x = 5 \tan(\dfrac{\pi}{3})y \]
Find the volume of solid formed by rotating the shaded region about the y-axis.
\[ V = \int_{0}^{1} \pi (5 \tan(\dfrac{\pi}{3})y)^{2} dy \]
\[= 25 \int_{0}^{1} \tan^{2} (\dfrac{\pi}{3} y) dy \]
Let:
\[\dfrac{\pi}{3}y = z , \dfrac{\pi}{3}dy \Rightarrow = dz \]
\[y=0 \Rightarrow z= 0\: and \: y =1 \Rightarrow z = \dfrac{\pi}{3} \]
\[V = 25\pi \int_{0}^{\dfrac{\pi}{3}} \tan ^{2} z (\dfrac{3}{\pi})dz = 75 \int_{0}^{\dfrac{\pi}{3}} \tan^{2} z \: dz \]
Since:
\[\sec ^{2} x – \tan ^{2} x = 1\]
\[=75 \int_{0}^{\dfrac{\pi}{3}} \sec^{2} z \: dz \:- 75\: \int_{0}^{\dfrac{\pi}{3}} 1 \:dz\]
\[ = 75 \tan z | _{0}^{\dfrac{\pi}{3}} – \: 75 z |_{0}^{\dfrac{\pi}{3}}\]
\[= 75 (\tan (\dfrac{\pi}{3}) – \tan 0) – \:75 (\dfrac{\pi}{3} – 0) \]
\[ = 75 (\sqrt {3} -0) – 75 \dfrac{\pi}{3} \]
\[= 75(\sqrt {3} – \dfrac{\pi}{3})\]
The volume of solid generated by revolving the shaded region is $ 75(\sqrt {3} – \dfrac{\pi}{3})$.
