
The aim of this question is to understand the solution of word problems related to simple algebraic expressions and the solution of a simple system of linear equations, and also the concept of maximizing or minimizing a given equation.

Positive number
To solve such word problems one has to simply convert the given constraints and conditions into one or more algebraic equations in one or more variables. to find a unique solution, the number of unknowns must be equal to the no. of consistent or independent, or unique algebraic equations.
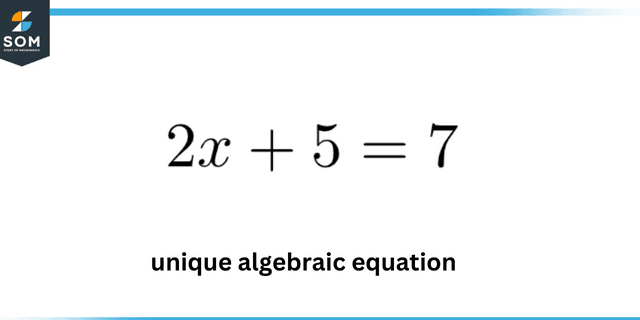
Unique algebraic equation
Once we have these equations, any method of solving linear equations or a system of linear equations may be deployed to find the unknown variables. Some well-known techniques include the substitution, echelon form of matrices, Crammer’s rule, etc.
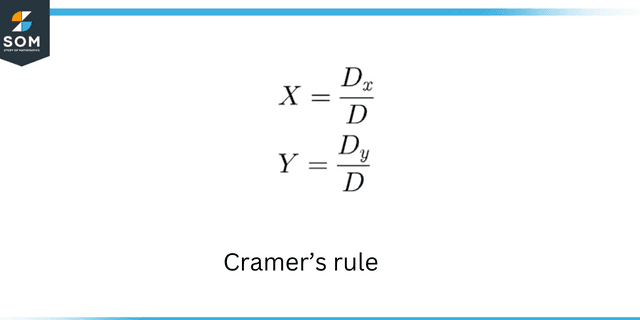
Cramers rule
To maximize the functions, we can deploy the differentiation method where we find the roots of the equation $ f^{ ‘ } ( x ) \ = \ 0 $.
Expert Answer
Let $ x $ and $ y $ be the two required positive real numbers. Under the given conditions and constraints:
\[ x \ + \ y \ = \ 110 \]
\[ y \ = \ 110 \ – \ x \ … \ …. \ … \ ( 1 ) \]
Now the product of $ x $ and $ y $ is given by the following formula:
\[ x y \ = \ x ( 110 \ – \ x ) \]
\[ x y \ = \ 110 x \ – \ x^{ 2 } \]
Since we need to maximize the product, let’s call it $ f( x ) $:
\[ f ( x ) \ = \ 110 x \ – \ x^{ 2 } \]
Differentiating both sides:
\[ f^{ ‘ } ( x ) \ = \ 110 \ – \ 2 x \]
Differentiating both sides:
\[ f^{ ” } ( x ) \ = \ – 2 \]
Since $ f^{ ” } ( x ) < 2 $, so the maxima exists at $ f^{ ‘ } ( x ) \ = \ 0 $:
\[ 110 \ – \ 2 x \ = \ 0 \]
\[ 110 \ = \ 2 x \]
\[ x \ = \ \dfrac{ 110 }{ 2 } \]
\[ x \ = \ 55 \]
Substituting this value in equation (1):
\[ y \ = \ 110 \ – \ ( 55 ) \]
\[ y \ = \ 55 \]
So the two numbers are $ 55 $ and $ 55 $.
Numerical Result
\[ x \ = \ 55 \]
\[ y \ = \ 55 \]
Example
If two numbers’ sum is equal to 600, maximize their product.
Let $ x $ and $ y $ be the two required positive real numbers. Under the given conditions and constraints:
\[ x \ + \ y \ = \ 600 \]
\[ y \ = \ 600 \ – \ x \ … \ …. \ … \ ( 2 ) \]
Now the product of $ x $ and $ y $ is given by the following formula:
\[ x y \ = \ x ( 600 \ – \ x ) \]
\[ x y \ = \ 600 x \ – \ x^{ 2 } \]
Since we need to maximize the product, let’s call it $ f( x ) $:
\[ f ( x ) \ = \ 600 x \ – \ x^{ 2 } \]
Differentiating both sides:
\[ f^{ ‘ } ( x ) \ = \ 600 \ – \ 2 x \]
Differentiating both sides:
\[ f^{ ” } ( x ) \ = \ – 2 \]
Since $ f^{ ” } ( x ) < 2 $, so the maxima exists at $ f^{ ‘ } ( x ) \ = \ 0 $:
\[ 600 \ – \ 2 x \ = \ 0 \]
\[ 600 \ = \ 2 x \]
\[ x \ = \ \dfrac{ 600 }{ 2 } \]
\[ x \ = \ 300 \]
Substituting this value in equation (1):
\[ y \ = \ 600 \ – \ ( 300 ) \]
\[ y \ = \ 300 \]
So the two numbers are $ 300 $ and $ 300 $.
