Greater Than or Equal to on a Number Line – A Beginner’s Guide

In the vast landscape of mathematical symbols, the “greater than or equal to” sign (≥) stands as a powerful tool to denote inclusivity and range.  When transposed onto a number line, this seemingly simple concept takes on a visual dimension, making abstract comparisons tangible and easy to comprehend.

In this article, we will embark on a journey through the realm of ≥, exploring its nuances and significance as it manifests on the number line. 

Defining Greater Than or Equal to on a Number Line

On a number line, the symbol “greater than or equal to” (denoted as ≥) signifies that a number, located at a particular point, is either greater than another specific number or exactly equal to it.

In visual terms, when a value $a$ is “greater than or equal to” a value $b$, the point representing $a$ lies to the right of or coincides with the point for $b$. Often, this relationship is indicated with a closed circle at the point representing $b$ and a line or arrow extending to the right, showing that all numbers in that direction, including $b$, satisfy the condition $a\ge b$. This visual representation aids in quickly grasping the relative positions and values of numbers in relation to one another.

Example

Solve the compound inequality: $2\le x+1\le 5$

Solution

Subtract 1 from all parts: $1\le x\le 4$

On a number line, this is represented by a closed dot at 1, a closed dot at 4, and a solid line connecting them, indicating all numbers in the inclusive range [1, 4].

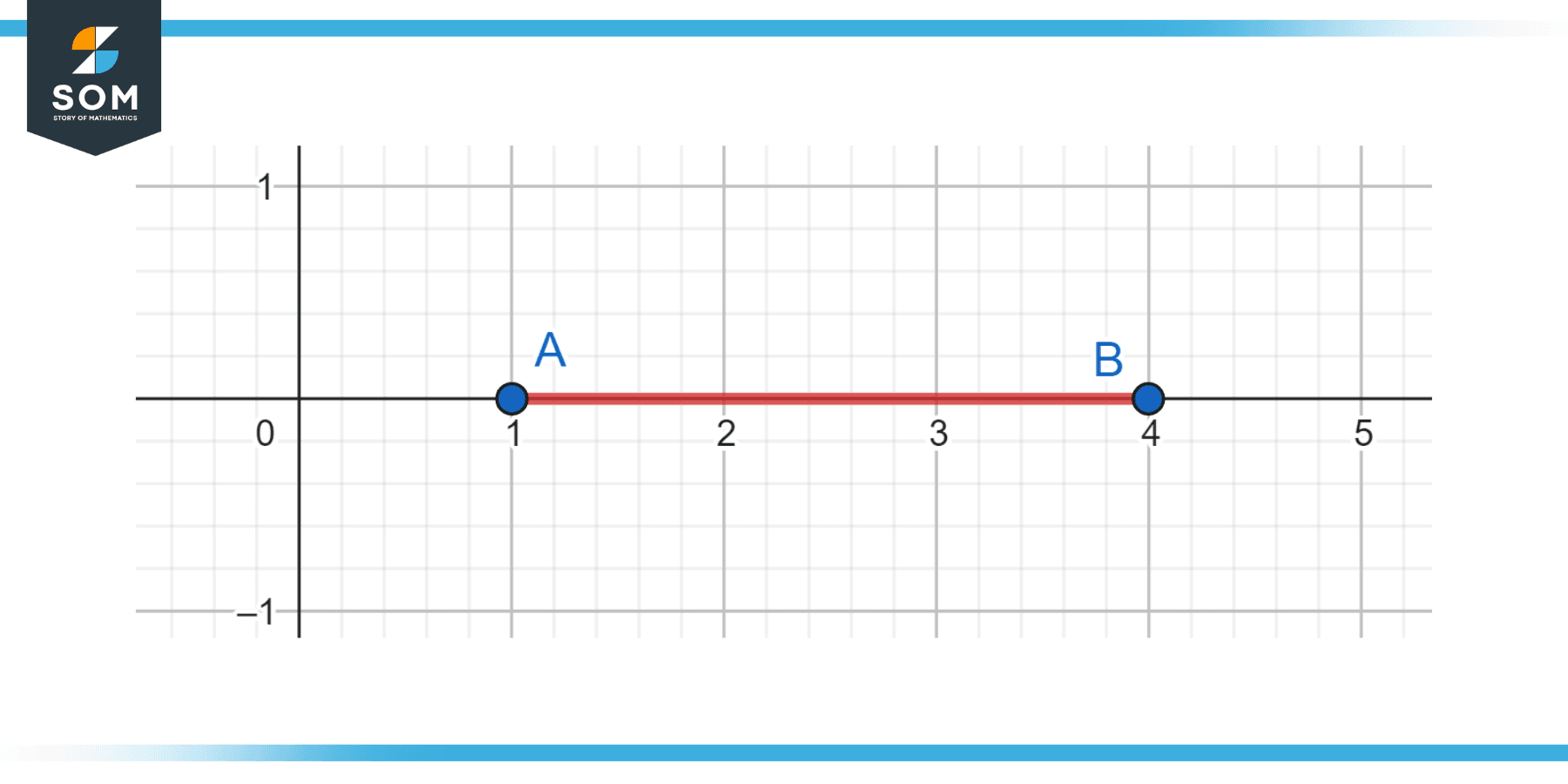
Figure-1.

Properties

The “greater than or equal to” symbol, represented as ≥, is a partial order relation on the real numbers. When visualized on a number line, this relation and its properties become evident. Let’s delve into these properties in the context of the number line:

1. Reflexivity:

   • Every number is greater than or equal to itself. Mathematically, for any number $a$, $a\ge a$. On a number line, this can be visualized as a point lying on itself.

2. Antisymmetry:

   • If $a$ is greater than or equal to $b$ and $b$ is greater than or equal to $a$, then $a$ must be equal to $b$. Mathematically, if $a\ge b$ and $b\ge a$, then $a=b$. This means that on a number line, the points representing $a$ and $b$ coincide.

3. Transitivity:

   • If $a$ is greater than or equal to $b$, and $b$ is greater than or equal to $c$, then $a$ is also greater than or equal to $c$. Mathematically, if $a\ge b$ and $b\ge c$, then $a\ge c$. On a number line, if $a$ lies to the right of $b$ and $b$ lies to the right of $c$, then $a$ will also lie to the right of $c$.

4. Addition and Subtraction Property:

   • If $a\ge b$, then $a+c\ge b+c$ and $a-c\ge b-c$ for any real number $c$. When you add or subtract a constant value to both numbers, their relative positions on the number line with respect to “greater than or equal to” don’t change.

5. Multiplication Property:

   • If $a\ge b$ and $c>0$, then $ac\ge bc$. If you multiply both sides of an inequality by a positive number, the inequality direction remains unchanged.
   • However, if $a\ge b$ and $c<0$, then $ac\le bc$. If you multiply both sides of an inequality by a negative number, the direction of the inequality flips. On a number line, this means the order of $a$ and $b$ will switch with respect to the origin when multiplied by a negative value.

6. Density Property:

   • For any two distinct real numbers $a$ and $b$ where $a<b$, there exists another real number $c$ such that $a<c<b$. This means that between any two points on the number line, there are infinitely many other points.

Exercise

Example 1

Solve the inequality: x + 3 ≥ 7

Solution

Subtract 3 from both sides: x ≥ 4

On a number line, this would be represented with a closed dot at 4 and a line or arrow extending to the right (indicating all numbers greater than or equal to 4).

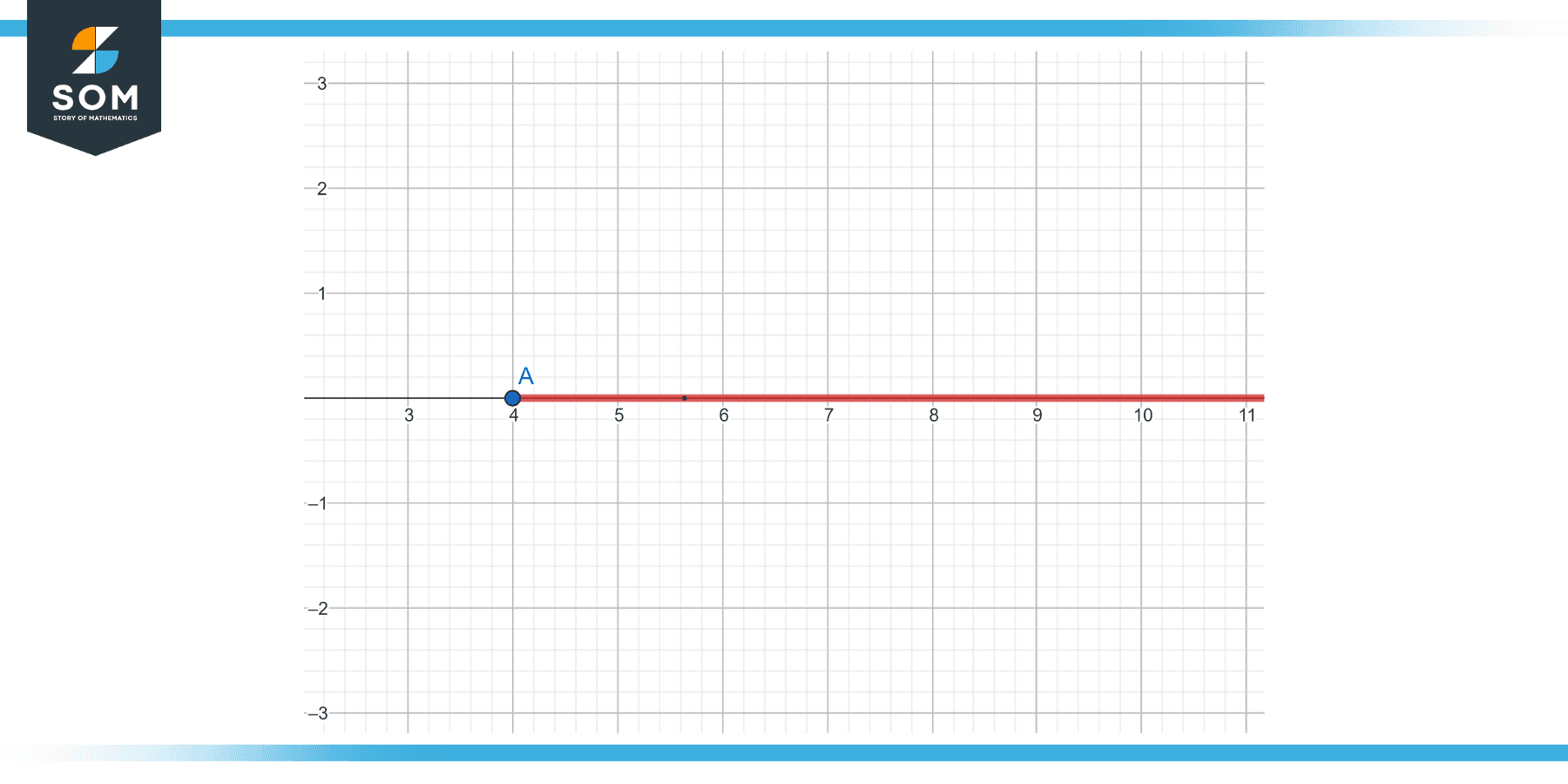
Figure-2.

Example 2

Solve the inequality: 2x – 5 ≥ 9

Solution

Add 5 to both sides: 2x ≥ 14

Divide by 2: x ≥ 7

On a number line, a closed dot at 7 with a line or arrow extending to the right.

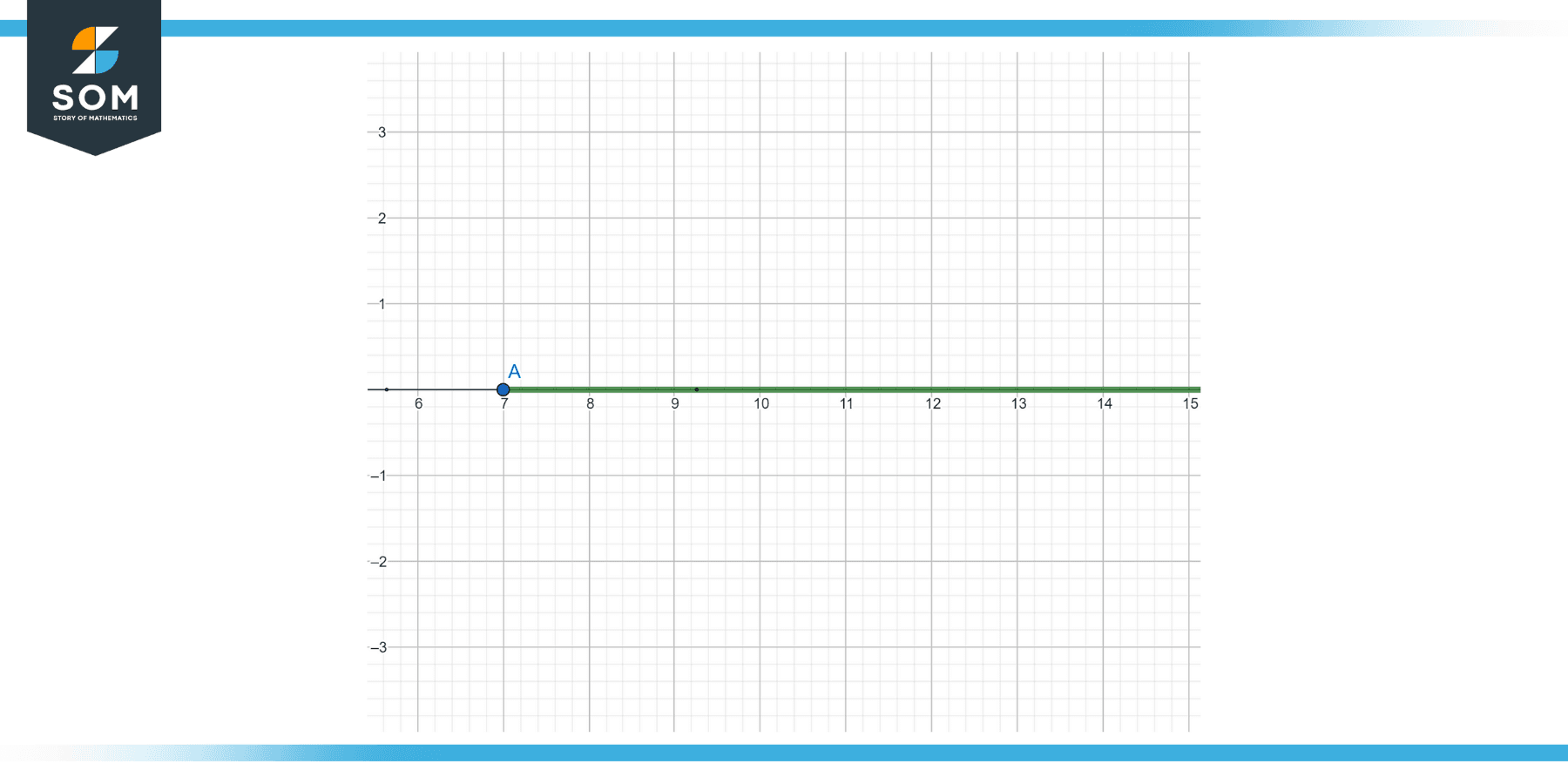
Figure-3.

Example 3

Solve the inequality: -3x + 2 ≥ 11

Solution

Subtract 2 from both sides: -3x ≥ 9

Divide by -3 (Remember to reverse the inequality when dividing by a negative number): x ≤ -3

On a number line, a closed dot at -3 with a line or arrow extending to the left.

Applications 

The “greater than or equal to” (≥) relation, especially when visualized on a number line, serves various functions across multiple fields. Here’s how this relation is applied across different disciplines:

1. Mathematics

   • Algebra: Inequalities are commonly used to solve problems involving limits, such as determining the range of possible values of a variable.
   • Calculus: In optimization problems, inequalities help determine the maximum or minimum values of functions within a given domain.

2. Economics and Finance

   • Budgeting: If a company’s earnings are greater than or equal to its expenditures, it is profitable or breaking even.
   • Stock Analysis: Investors might use inequalities to set benchmark performances. For example, they might look for stocks with returns ≥ 8%.
   • Linear Programming: This mathematical modeling technique uses inequalities to determine the best outcome (such as maximum profit or minimum cost) in a given mathematical model.

3. Computer Science

   • Algorithms: Many algorithms, especially sorting and searching ones, use the ≥ relation for making decisions.
   • Database Queries: When filtering or searching through large datasets, queries often involve ≥ conditions to retrieve relevant records.

4. Physical Sciences

   • Physics: Inequalities might be used to set bounds on measurements, like ensuring a particle’s speed is less than or equal to the speed of light.
   • Chemistry: In equilibrium reactions, chemists might look for conditions where the concentration of one substance is greater than or equal to another.

5. Engineering

   • Safety Standards: Structures are often designed to withstand loads greater than or equal to the maximum expected load to ensure safety.
   • Signal Processing: Filters might be designed to allow frequencies greater than or equal to a certain threshold to pass through.

6. Medicine and Biology

   • Epidemiology: Researchers might track if the number of cases of a disease is greater than or equal to a threshold that requires intervention.
   • Pharmacology: Dosages might be recommended if a patient’s weight is greater than or equal to a certain number.

All images were created with GeoGebra.