How to Name a Plane in Geometry?

To name a plane, three non-collinear points should be present on a two-dimensional flat surface.

In geometry, a plane is considered a two-dimensional surface with no boundaries. If points A, B and C are present in two-dimensional flat surfaces, then we can call the plane ABC or the whole surface” P”. Hence, a plane is named either by combining three non-collinear points or represented by a capital letter.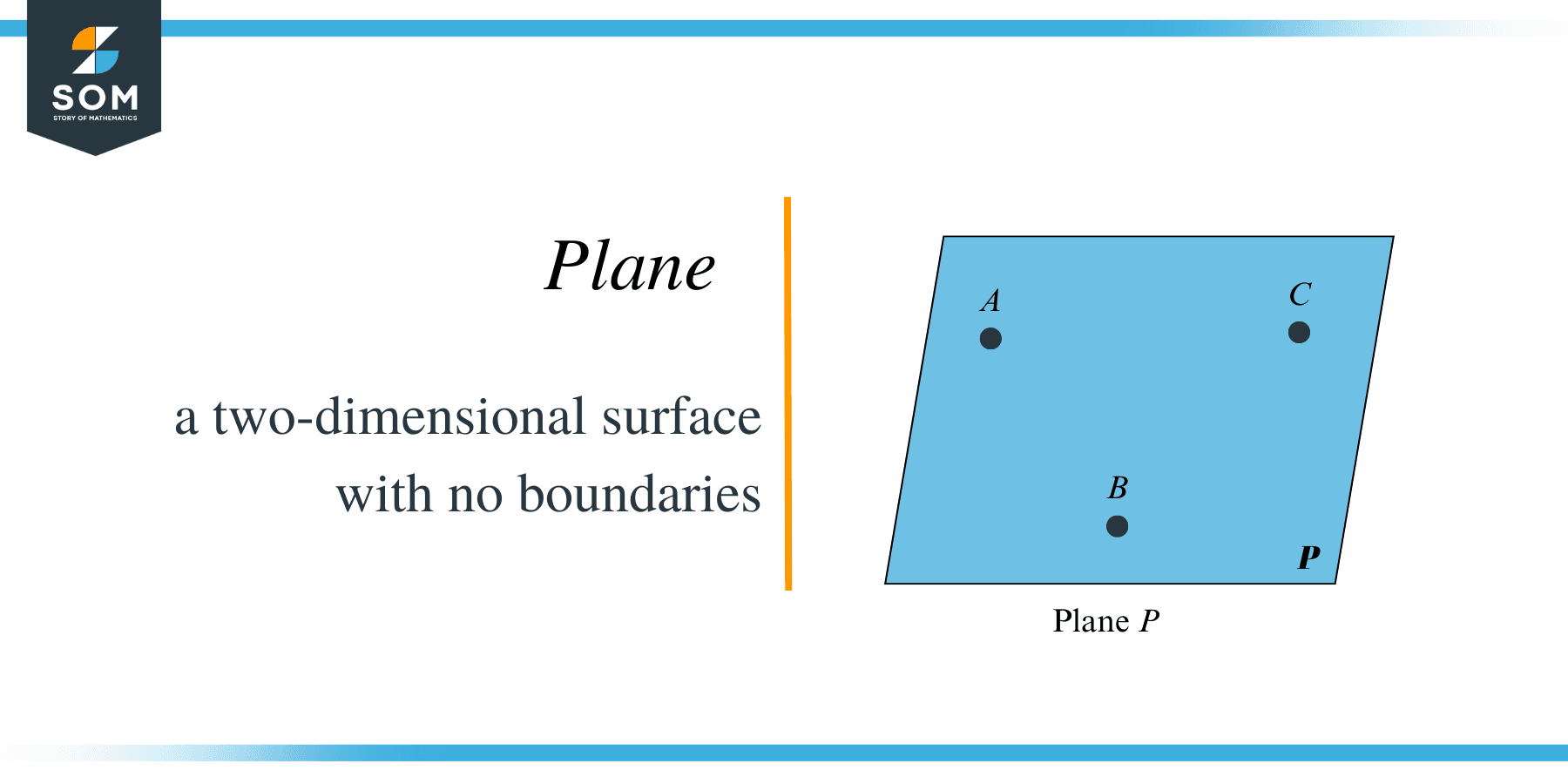

In this article, we will discuss what a plane means, its types and how to name the plane.

How to Name a Plane in Geometry?

A plane is named by combining three non-collinear points or by labelling it with a capital letter such as “S”, “P”, or “T”.

Naming Planes

A commonly asked question is how to name a plane in 2 different ways. A plane can be named by labelling the plane with a capital letter. Any flat surface with infinite boundaries is called a plane, and it can be named “S”, “P”, or “T”. We should capitalize the letter, or we can name the plane with a combination of three non-collinear points which are present in the plane.

For example, consider the picture below. There are six points in total, but we can name the plane only as ABC, ABD and ACD. The question arises why is that so? Why can we not name the plane BCD or HGD? To answer these questions, we need to know what a plane actually is and what are the properties and types of the plane.

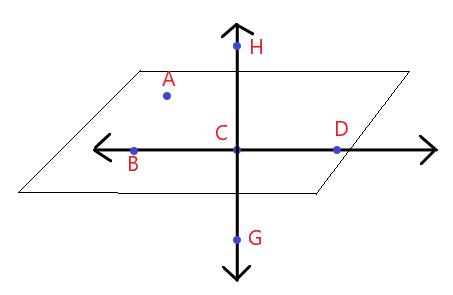
What Is a Plane?

In geometry, a plane is an infinite two-dimensional flat surface. The plane’s surface is considered non-thick with zero curvature, and the boundaries are undefined or unlimited.

A commonly asked question can we see a plane in real life? Well, it is impossible to see a plane as we already said, it does not have any boundaries, but we can imagine some surfaces to be considered a plane if they are not limited by boundaries. For example, the flat surfaces of a square, cube or piece of paper are considered real-life examples of a plane if the boundaries are considered infinite.

Let us now model a concept of a plane in the shape of a geometrical figure. As there are no real-life examples, we will take a flat piece of paper and draw a parallelogram on it along with many lines, which shows the infinite nature of the surface because lines are infinite and have no depth or curvature, just like a plane.

Suppose we have drawn the parallelogram on a two-dimensional surface. Remember that we can also draw a plane on a three-dimensional surface, but we will keep our discussion related to the two-dimensional systems in this topic. As discussed earlier, a plane consists of three non-collinear points, so if we plot three points in the parallelogram so that those points do not lie on the same line, then we will say that this parallelogram represents a plane.

Identifying a Plane in Geometry

Identifying a plane is easy as we need to identify a flat surface with multiple points in it. So how many points are required to name a plane? As already discussed, a flat surface having three non-collinear points is a plane. Can a flat surface with 2 or 4 points be called a plane, or how to name a plane with 4 points?

Let us answer these questions one by one; why can a plane not have two non-collinear points? Because the 2 points are always collinear and you can draw a straight line by connecting two points no matter where they are present in a plane, as shown in the picture below.

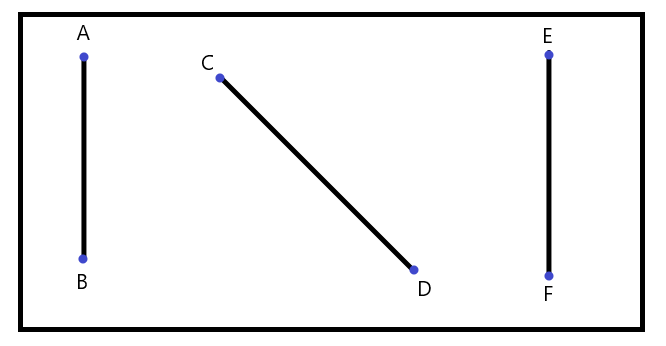
Now to the second question, why can’t a plane consist of four non-collinear points? If we take two points, then it gives a 1-dimensional line which we can rotate in a plane, and if we add a third point which is collinear to the previous two points, then infinite planes can pass through these points. But if the three points are non-collinear, then one and only one plane can pass through it. So what happens when we add the fourth point in the plane is that either the point will be coplanar with other given points or it will not lie in the plane, simple as that.

When we add the fourth point, then it can either be coplanar or non-coplanar; if it is not coplanar, then it is not even on the plane. But suppose it is coplanar and the plane passes through it along with the first two points, then the plane will not pass through the previous third point. Hence, we only take three non-collinear but coplanar points for a plane.

Just for fun’s sake, let’s take an example of a tripod. We know it has three legs, and even if they are not equal in length, the tripod works just fine. It does not wobble much, but the moment we add the fourth leg, it starts to wobble; the same is true with the plane. A single plane can pass through only three non-collinear but coplanar points.

Types of Planes

There are two types of planes in geometry: a) Parallel Plane and b) Planes that intersect.

Parallel Planes: The planes that do not intersect are known as parallel planes. For example, the floor and ceiling of a room with indefinite boundaries can be considered parallel planes. Similarly, walls on both sides of the room can also be considered parallel planes. We can show parallel planes as:

Intersecting Planes: These are the planes which intersect with each other. These planes are perpendicular to each other, meaning one plane passes through the second plane at $90^{o}$. The planes cannot intersect with each other for more than one line. This means that only a single line will be common between the two planes. For example, Planes S and A intersect, and the common line between them is line XY, as shown in the picture below.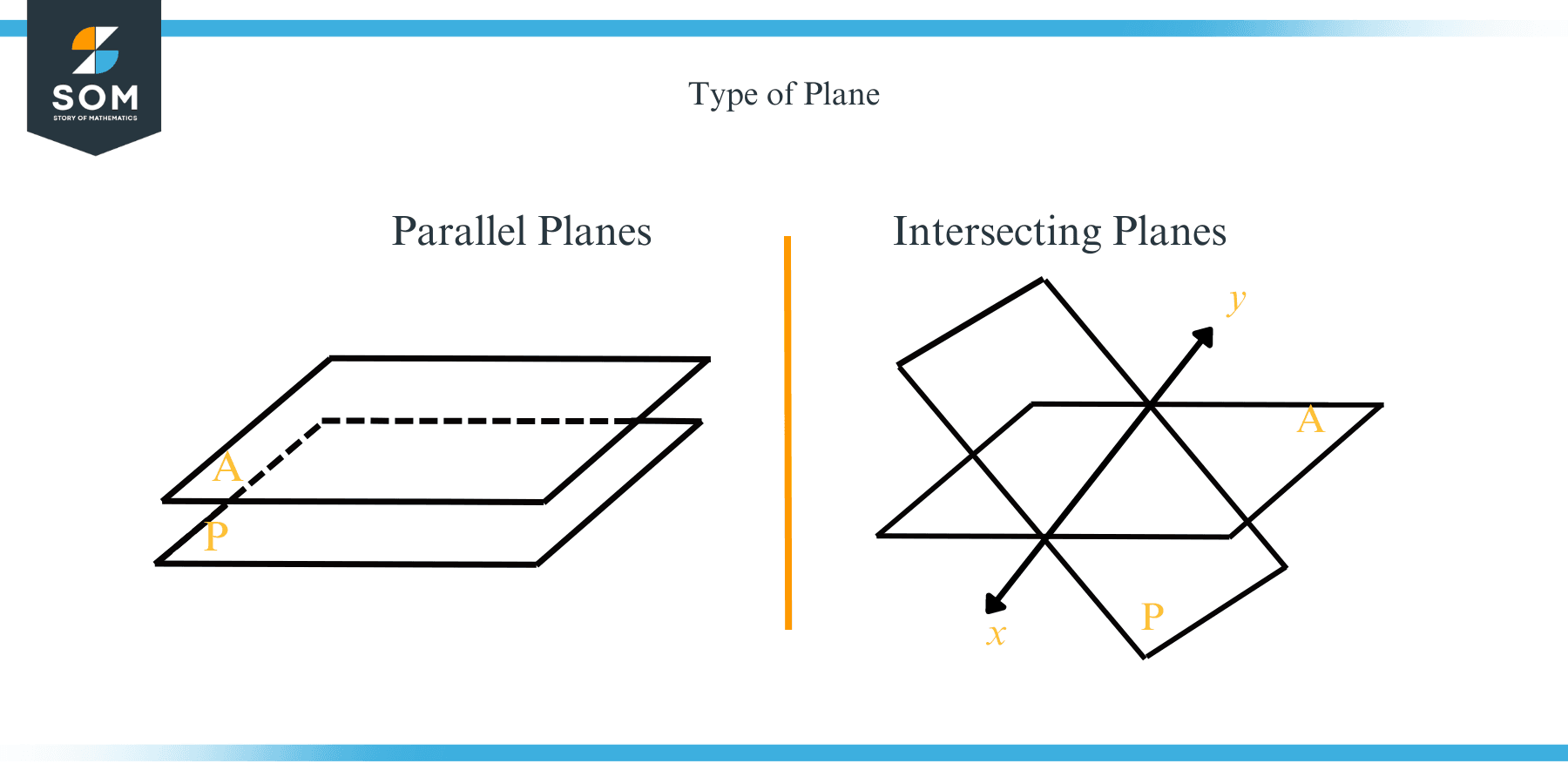

Properties of a Plane

The properties of a plane are given below.

1. A plane consists of three coplanar points which do not lie on the same line. Hence, the points of a plane are non-collinear.
2. The line can either be perpendicular, parallel or lie in the plane.
3. If there are two planes, they can either be parallel or perpendicular to each other.
4. If two lines are perpendicular against the same plane, then these two lines will be parallel to each other.
5. If two distinct planes are perpendicular against a common line, then these two planes must be parallel to each other.

Example 1: A teacher has drawn a plane on the whiteboard and has asked Mason to name the plane while also mentioning the coplanar and collinear points. Help Mason answer the question.

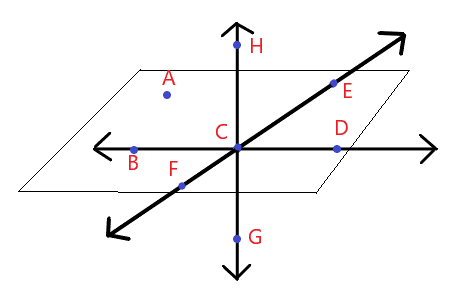
Solution:

The name of the plane can be ACF, ACE, ABC, ACD, ECD, ECB. 

Example 2: Name the plane for the image given below.

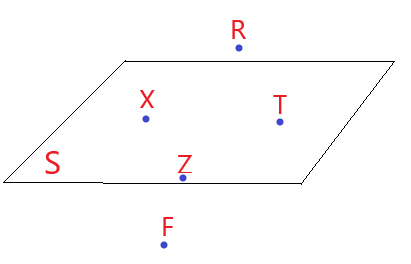
Solution:

The name of the plane is XZT as the rest of the points are not coplanar.

Important Definitions

Point

A point is used in geometry to get a coordinate plane’s location. The point has no direction, width or dimension. It is denoted as a dot on a plane.

Coplanar Points

In plane geometry, the points which lie on the same plane are called coplanar points. For example, we know that three points lie on the plane; hence these points are called coplanar points.

Collinear Points

The points which lie on the same line are called collinear points. For a plane to exist, three points cannot be collinear.

Line

A line is formed by combining at least two points. The line is considered to be infinite; hence we can say that line consists of a combination of infinite points.

If we make the line finite, then it is called a line segment, not a complete line. The lines that intersect each other are known as intersecting lines or perpendicular lines, and lines that do not intersect are known as parallel lines.

Frequently Asked Questions

What Is Used to Name a Point in Geometry?

Any dot or point on a plane which shows a location can be named by a letter. Hence, a dot can be named “A”, “B”, or “C”. When three non-collinear points are present on a flat surface, then we say it is a plane, and it can be named by those three non-collinear points or by any capital letter.

A line is named after the combination of two endpoints. If one endpoint is A and the other is B, then the line is named AB.

Conclusion

After reading this article, you now know how a plane is formed, its characteristics, and how to name a plane. Let us discuss the summary of the article and what we have learned so far in the points given below.

• The plane consists of three coplanar points that are non-collinear. These points never lie on the same line.

• The name of the plane is given by either combining the three points in the plane or by labelling it with a capital letter.

• Parallel planes and intersecting ones are labelled separately. Parallel planes do not cross each other, while the intersection planes cross each other through a common line.

Now you now know all about plane types and, more importantly, how to name a given plane.