JUMP TO TOPIC

Embarking on a journey through space and dimensions, vector translation is a fundamental tool for manipulating and transforming geometric objects with precision and accuracy.
This transformative technology enables us to displace and relocate vectors while preserving their direction and magnitude. It is key to unlocking many practical applications in various fields, from computer graphics and robotics to physics and engineering.
In this article, we delve into the enchanting realm of vector translation, unraveling its underlying concepts, exploring its versatile applications, and uncovering the secrets behind its remarkable ability to reshape our perception of space.
Definition of Vector Translation
Vector translation, also known as vector displacement, refers to a geometric transformation that involves shifting or moving a vector from its initial position to a new position while maintaining its original direction and magnitude.
It involves adding a displacement vector to the original vector, resulting in a new vector representing the translated position. By applying vector translation, objects or points in space can be repositioned without altering their orientation or size, allowing for precise and controlled movements within a coordinate system.
This fundamental concept is a building block for various mathematical operations and has wide-ranging applications in fields such as computer graphics, physics, engineering, and robotics. below in the figure-1, we present a generic representation of the vector translation.
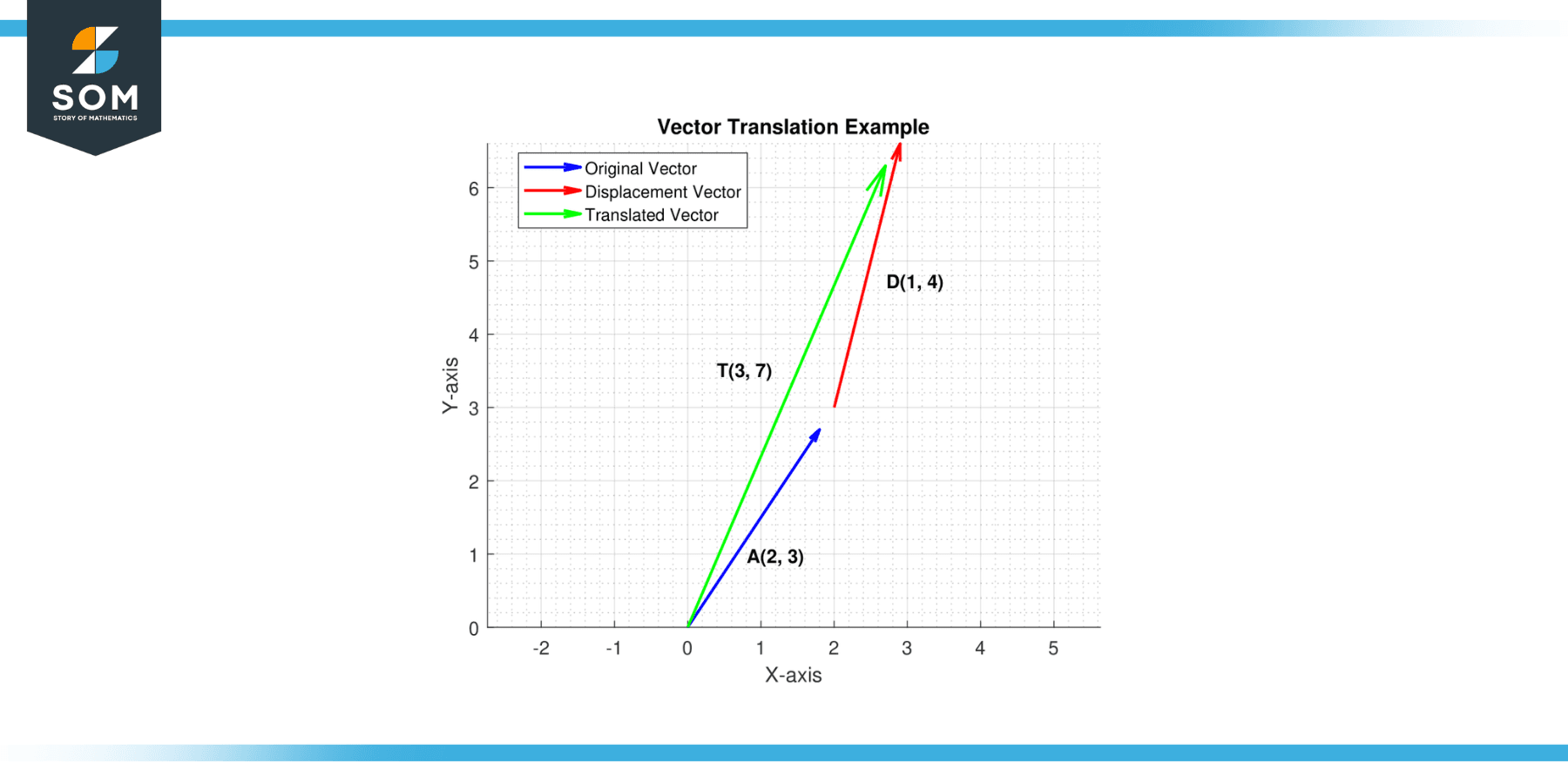
Figure-1.
Process of Vector Translation
The process of vector translation involves several steps to accurately move a vector from its original position to a new position while preserving its direction and magnitude. Here are the steps involved:
Define the Original Vector
Begin by identifying the original vector that needs to be translated. The vector is typically represented as an ordered set of components or coordinates, such as (x, y) in two dimensions or (x, y, z) in three dimensions.
Determine the Displacement Vector
Determine the displacement vector representing the desired movement or shift from the original position. The displacement vector specifies the direction and magnitude of the translation. It is often represented as a separate vector, denoted as (dx, dy) or (dx, dy, dz), where dx, dy, and dz represent the respective displacements along each coordinate axis.
Add the Vectors
Perform vector addition by adding the corresponding components of the original vector and the displacement vector. If the original vector is represented as A = (a1, a2, a3) and the displacement vector is represented as D = (dx, dy, dz), the translated vector T is obtained by adding the corresponding components: T = A + D = (a1 + dx, a2 + dy, a3 + dz).
Simplify the Result
Simplify the resulting translated vector by combining like terms and representing it in its simplest form. This involves evaluating the addition operation and simplifying any numerical expressions.
Interpret the Translated Vector
Analyze the translated vector to understand its meaning in the given context. Consider the direction and magnitude of the translated vector and interpret it within the coordinate system or the problem domain. The translated vector represents the new position or displacement of the original vector.
It’s important to note that the process of vector translation can be extended to higher dimensions by considering additional components for each vector and displacement. The steps remain the same, with the addition operation involving the corresponding components of the vectors.
Properties
Vector translation possesses several important properties that define its nature and behavior. Let’s explore these properties in detail:
Direction Preservation
Vector translation preserves the direction of the vector being translated. Regardless of the magnitude or position of the vector, the direction remains unchanged throughout the translation process. This property ensures that the orientation of objects or points in space is maintained during the transformation.
Magnitude Preservation
Similar to direction, the magnitude of the vector remains unchanged during translation. The length or size of the vector remains constant throughout the process, ensuring that the object being translated retains its original scale or size.
Commutativity
Vector translation exhibits the property of commutativity, which means that the order of vector translations does not affect the final result. In other words, if vectors A and B are translated in sequence, the result will be the same regardless of whether A is translated first and then B or vice versa. Mathematically, this can be represented as A + B = B + A.
Associativity
Vector translation also follows the property of associativity, meaning that the grouping of translations does not affect the final result. If vectors A, B, and C are translated in sequence, the order in which these translations are grouped (i.e., (A + B) + C or A + (B + C)) will not alter the final translated vector. Mathematically, this can be represented as (A + B) + C = A + (B + C).
Zero Vector
The translation of the zero vector results in the zero vector itself. This property implies that translating an object by a zero vector has no effect, as it does not cause displacement or movement.
Inverse Translation
Every vector translation has an inverse translation that “undoes” the original translation. The inverse translation is obtained by negating the displacement vector. When the inverse translation translates the original vector, it returns to its original position. Mathematically, if vector A is translated by vector B, then translating the resulting vector by -B will return it to its original position.
Linearity
Vector translation exhibits the property of linearity. This means that when two or more translations are combined, the resulting translation is equivalent to the sum of the individual translations. Mathematically, if vector A is translated by vector B and then translated by vector C, the resulting translation is equivalent to translating vector A directly by the sum of vectors B and C.
Applications
Vector translation, also known as vector displacement, finds applications in various fields. Here are some notable examples:
Computer Graphics
Vector translation is fundamental for rendering and manipulating 2D and 3D objects. In a virtual environment, objects can be moved, rotated, and scaled by vector translation. This enables the creation of animations, simulations, and interactive graphics used in video games, virtual reality, computer-aided design (CAD), and computer-generated imagery (CGI) for movies.
Robotics and Automation
In robotics, vector translation is essential for motion planning and control. By translating vectors representing the positions and orientations of robotic limbs or end effectors, precise movements can be achieved. This enables robots to perform pick-and-place operations, assembly line operations, and autonomous navigation in various industries, including manufacturing, healthcare, and logistics.
Physics and Engineering
In physics and engineering, vector translation is employed to describe and analyze the motion of objects. It is used to calculate particles’ displacement, velocity, acceleration, and the movement of forces and momentum. This aids in understanding and predicting the behavior of physical systems, ranging from simple mechanical systems to complex fluid dynamics and electromagnetic fields.
Computer Vision
In computer vision, vector translation is used for image registration, alignment, and tracking. By translating image features or points of interest, images or video frames can be aligned to facilitate tasks such as image stitching, object tracking, and motion estimation. This has applications in surveillance, object recognition, augmented reality, and medical imaging.
Geographical Information Systems (GIS)
GIS relies on vector translation to represent and manipulate geographic data accurately. The positions of objects or geographic entities can be updated or adjusted by translating vectors representing spatial features, such as points, lines, and polygons. This aids in tasks like map projections, spatial analysis, and route planning for applications in urban planning, environmental monitoring, and navigation systems.
Structural Analysis and Finite Element Analysis (FEA)
In structural engineering, vector translation is utilized to model and analyze the behavior of structures subjected to loads and deformations. By translating vectors representing forces or displacements, engineers can analyze the response of structures, evaluate stresses and strains, and optimize designs for safety and efficiency. FEA software relies on vector translation algorithms to solve complex structural problems.
Satellite Communication and Global Positioning System (GPS)
In satellite communication systems, vector translation is used for accurate position determination and navigation. GPS receivers can calculate precise user positions on Earth’s surface by translating vectors representing satellite positions and velocities. This has applications in navigation, surveying, mapping, and tracking moving objects.
Machine Learning and Data Analysis
In machine learning and data analysis, vector translation is utilized for data preprocessing and feature engineering. By translating vectors representing data points or variables, the distribution and relationships between data can be adjusted or aligned, enhancing the performance of machine learning algorithms and facilitating data analysis tasks such as clustering, dimensionality reduction, and pattern recognition.
Exercise
Example 1
Consider a vector v = (3, -2) in a two-dimensional coordinate system. Translate this vector by a displacement vector u = (1, 4).
Solution
To translate the vector v by the displacement vector u, we add the two vectors together:
v + u = (3, -2) + (1, 4)
v + u = (4, 2)
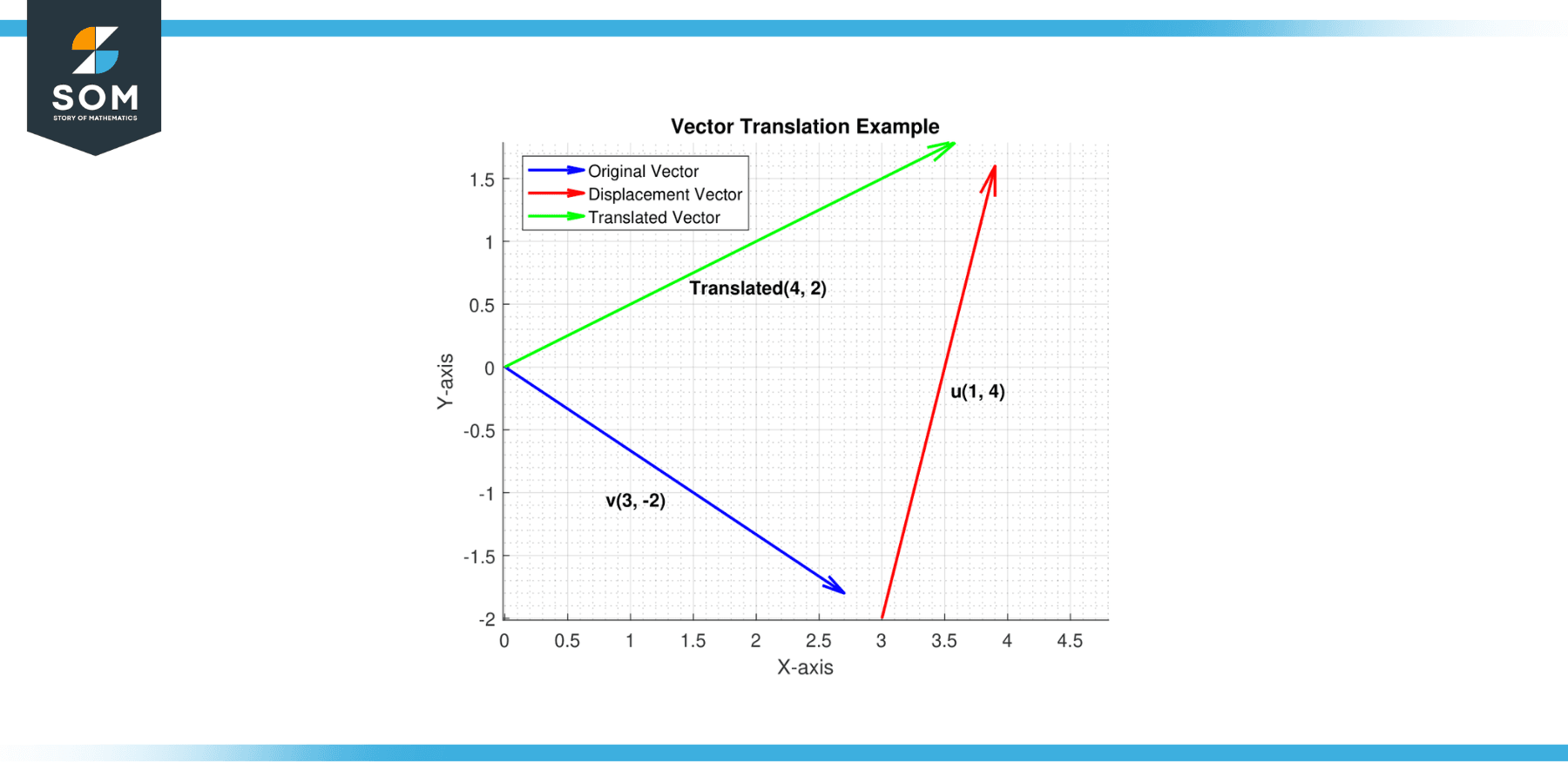
Figure-2.
Example 2
Let vector A = (5, 7) be translated by vector B = (-2, 3). Find the resulting translated vector.
Solution
The translated vector is obtained by adding the two vectors together:
A + B = (5, 7) + (-2, 3)
A + B = (5 + (-2), 7 + 3)
A + B = (3, 10)
Example 3
Suppose vector P = (2, -4) is translated by vector Q = (3, 1). Determine the translated vector.
Solution
The addition of the two vectors gives the translated vector:
P + Q = (2, -4) + (3, 1)
P + Q = (2 + 3, -4 + 1)
P + Q = (5, -3)
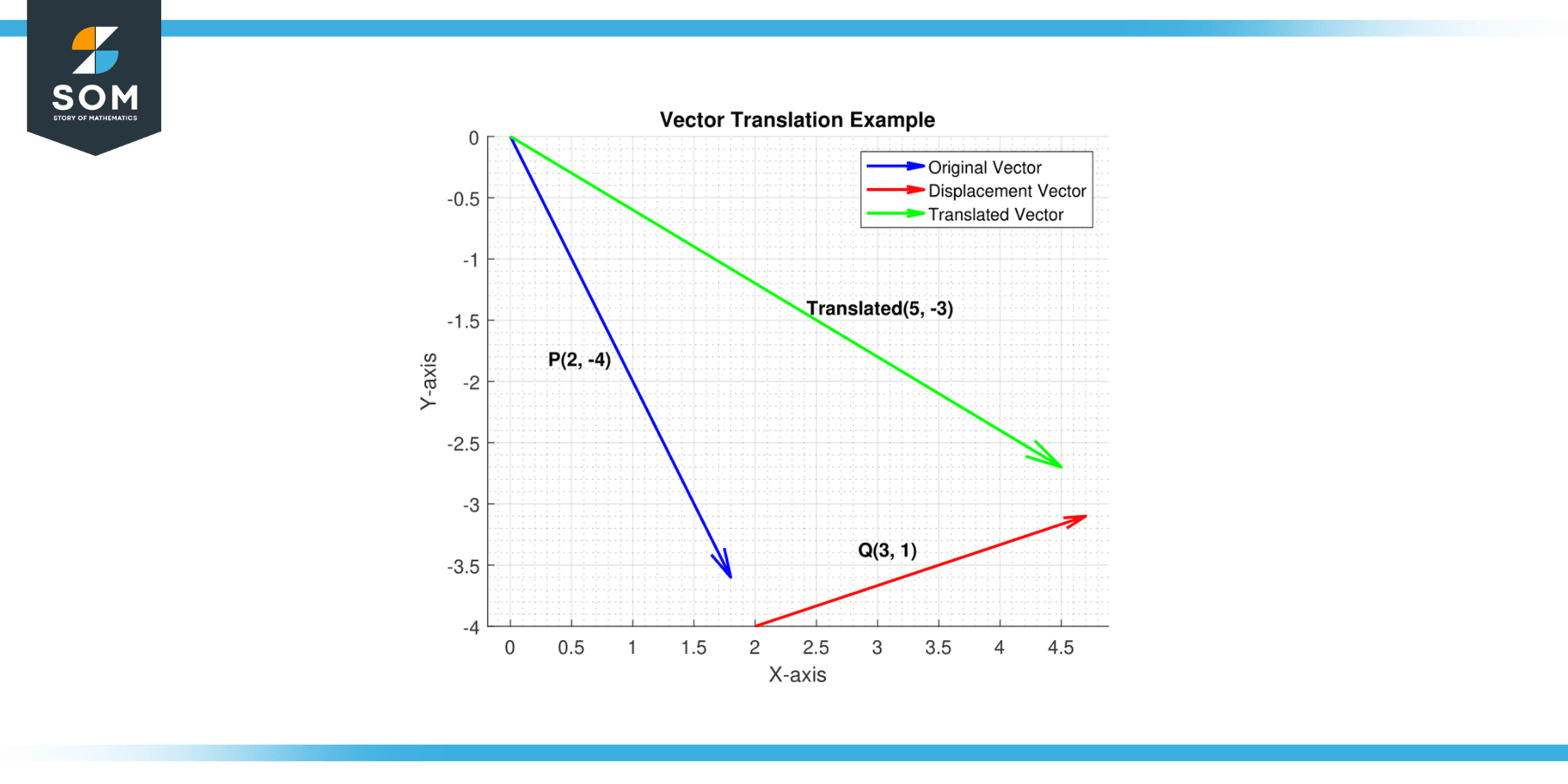
Figure-3.
Example 4
Given vector X = (8, -6) and its translation vector Y = (-4, 2), calculate the resulting translated vector.
Solution
To find the translated vector, we add the two vectors together:
X + Y = (8, -6) + (-4, 2)
X + Y = (8 – 4, -6 + 2)
X + Y = (4, -4)
Example 5
Let vector M = (1, 2, -3) be translated by vector N = (-2, 0, 4). Determine the translated vector.
Solution
The translated vector is obtained by adding the two vectors together:
M + N = (1, 2, -3) + (-2, 0, 4)
M + N = (1 – 2, 2 + 0, -3 + 4)
M + N = (-1, 2, 1)
All images were created with GeoGebra and MATLAB.
