How to Find Hypotenuse With Angle and Side – A Complete Guide

Geometry, with its intricate shapes and precise calculations, has always been at the heart of architectural marvels, spacecraft trajectories, and even simple everyday tools. What if you’re armed with the knowledge of just one side and an angle? How to find hypotenuse with angle and side? This article guides you through the process of finding the hypotenuse using just an angle and one side.

How to Find Hypotenuse With Angle and Side

To find a hypotenuse with an angle and a side we can use the sin and cosine ratios, depending upon which side has been given to for finding the hypotenuse.  The ratios are given as:

$\text{sin}(\theta )$hypotenuse

cos(θ) = hypotenuse / adjacent

Delving deeper in how to find a hypotenuse with angle and side we first need to understand the right triangle, let’s first dive into understanding the right triangle.

Understanding Right Triangles

Before diving in, let’s quickly recap the essentials of right triangles. A right triangle comprises three sides: the hypotenuse (the longest side opposite the right angle), and the two other sides often referred to as the adjacent and opposite sides, relative to a specific angle in the triangle. The angles, besides the right angle, are acute and sum up to 90 degrees.

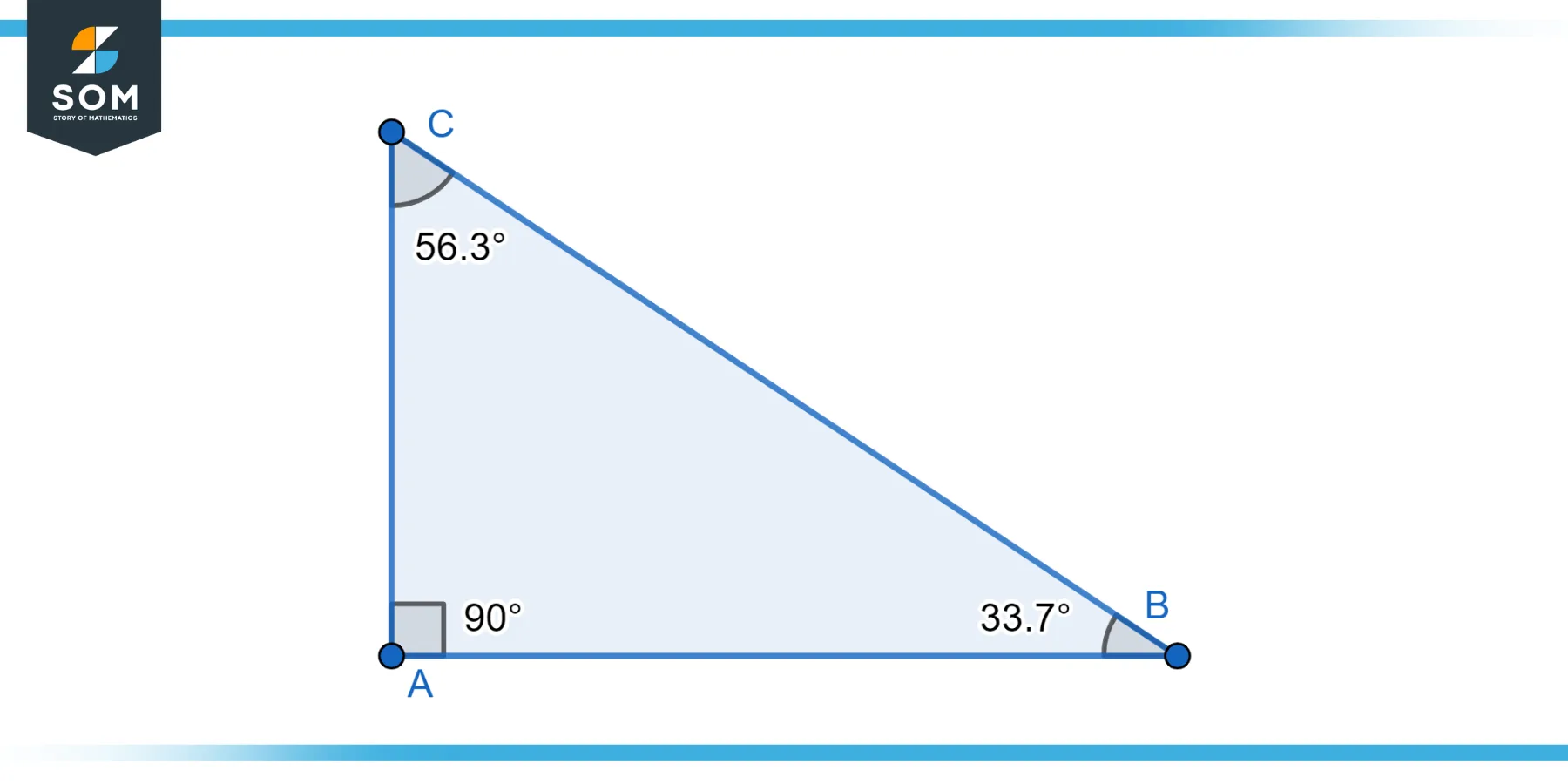
Figure-1.

Trigonometry to the Rescue

Trigonometry, a branch of mathematics, deals with the relationships between the sides and angles of triangles. It introduces us to three primary ratios:

• Sine (abbreviated as sin)
• Cosine (cos)
• Tangent (tan)

For a given angle θ in a right triangle

$\text{sin}(\theta )$hypotenuse

cos(θ) = hypotenuse / adjacent​

tan(θ) =adjacent / opposite​

With these tools in our arsenal, let’s find the hypotenuse!

Case Study

Finding the Hypotenuse With Given Angle and Side

Scenario 1

Given the opposite side and an angle. Suppose you’re given that the opposite side (let’s call it a) is 5 units and θ is 30 degrees. To find the hypotenuse (H):

Use the sin ratio:

sin(30∘) = 5 / H​

Given that sin(30∘) = 0.5 (from trigonometric tables or calculators): 0.5 = 5 / H​ Thus:

$H=10$ units.

Scenario 2

Given the adjacent side and an angle. If you know the adjacent side (let’s name it b) is 6 units and θ is 45 degrees, employ the cosine ratio:

cos(45∘) = 6 / H​

Given that cos(45∘) = 0.7071:

0.7071 = 6 / H​

Resulting in $H\approx 8.49$ units.

These scenarios illuminate how just an angle and a side can empower us to determine the length of the hypotenuse with relative ease.

Exercise 

Example 1

Given: Side $a$ (opposite side) = 5 units, Angle $\theta$ = 30 degrees. Find the hypotenuse ($H$).

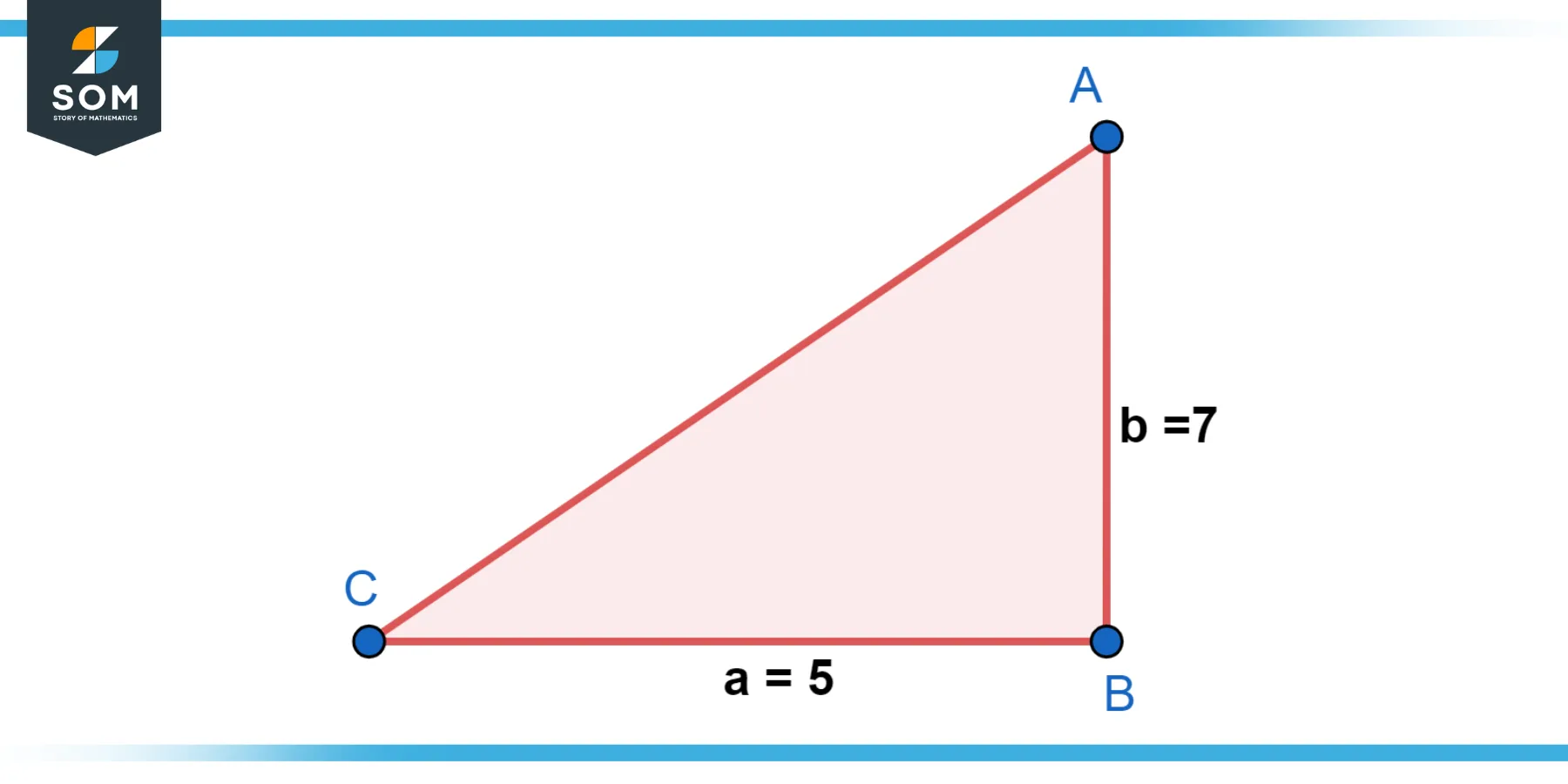
Figure-2.

Solution

Using the sine function:
sin(30∘) = a / H​
1 / 2​ = 5 / H​

$H=10$ units

Example 2

Given: Side $b$ (adjacent side) = 8 units, Angle $\theta$ = 45 degrees.

Solution

Using the cosine function:
cos(45∘) = b / H​
1 / $\sqrt{2}$​ = 8 / H​
$H\approx 11.31$ units

Example 3

Given: Side $a$ (opposite side) = 12 units, Angle $\theta$ = 60 degrees.

Solution

Using the sine function:
in(60∘) = a / H​
$\sqrt{2}$ / 2 ​​= 12 / H​
$H\approx 13.86$ units

Example 4

Given: Side $b$ (adjacent side) = 15 units, Angle $\theta$ = 30 degrees.

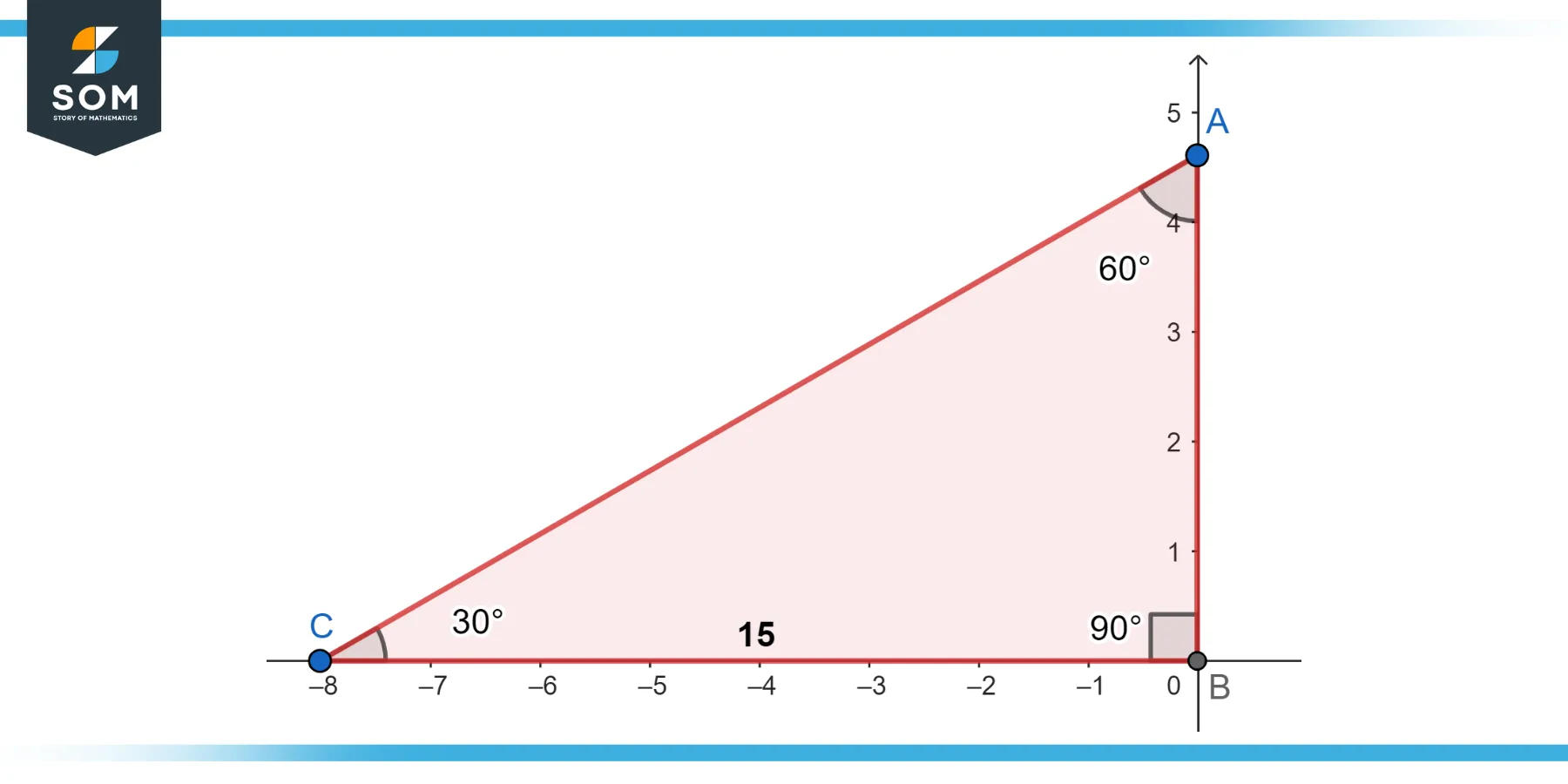
Figure-3.

Solution

Using the cosine function:
cos(30∘) = b / H​
$\sqrt{2}$ / 2​​ = 15 / H​
$H\approx 17.32$ units

Example 5

Given: Side $a$ (opposite side) = 20 units, Angle $\theta$ = 45 degrees.

Solution

Using the sine function:
sin(45∘) = a / H​
1 / $\sqrt{2}$​= 20 / H​
$H\approx 28.28$ units.

Applications 

Discovering the hypotenuse of a right triangle using only an angle and a side might seem like a mathematical exercise reserved for the classroom. However, this fundamental principle of trigonometry has broad implications across multiple industries and daily life. Let’s delve into how this geometric concept is intertwined with our world.

Architecture and Construction

When architects design buildings or structures, they often deal with non-orthogonal shapes and angles. For example, in constructing a sloped roof, knowing one side of the roof and the desired angle of inclination can help determine the length of the roof’s slope (the hypotenuse). This understanding aids in material estimation, structural integrity calculations, and aesthetic considerations.

Aviation

Pilots and air traffic controllers need to be acutely aware of distances and angles. When an aircraft ascends or descends, knowing the angle of ascent or descent and the horizontal distance covered can help determine the aircraft’s altitude change (the hypotenuse). Accurate calculations are crucial for safety and efficient flight paths.

Navigation and Cartography

Mariners and cartographers use trigonometry for plotting courses. Suppose a ship needs to avoid an obstacle. Knowing the distance they’ve traveled in a particular direction (one side) and the angle they’ve deviated can help determine the direct line distance (hypotenuse) they are from their original point.

Telecommunication

In the realm of wireless communication, the angle of a satellite dish or an antenna in relation to the ground and the height of the installation can determine the direct line of sight or the hypotenuse distance to the satellite or receiving station. This direct line ensures optimal signal reception.

Astronomy

Astronomers, when measuring the distance between celestial objects or the distance of a star from Earth, often work with angular measurements. A known side (like the radius of Earth’s orbit) and an observed angle can help estimate vast interstellar distances using the principles of trigonometry.

Sports

Think of a soccer player planning a free kick. Knowing the distance to the goal and the angle they want to give the ball can determine the arc or path (hypotenuse) the ball should follow to bypass the wall and score.

Geography and Geology

Geologists studying landforms, such as mountains or valleys, can determine the length of a slope by knowing the base distance and the angle of elevation or depression. This knowledge aids in various applications, including understanding erosion patterns or planning road constructions.

Forensic Science

Crime scene investigators sometimes rely on trigonometry to reconstruct incidents. For instance, knowing the angle at which a bullet was fired and the height difference between the shooter and the victim can determine the shooter’s distance from the victim.

Art and Design

Artists and graphic designers use the principles of perspective, where lines converge at a vanishing point, creating depth. Understanding angles and sides allows them to accurately depict three-dimensional objects on a two-dimensional surface.

Daily Life

Picture this: you’ve got a ladder, and you want to place it against a wall to reach a specific height, but there’s a garden bed in the way. How far should the ladder’s base be from the wall, and at what angle should it lean to ensure stability and reach? This everyday problem can be addressed using our knowledge of angles, sides, and the hypotenuse.

All images were created with GeoGebra.