JUMP TO TOPIC

A heptagon is a geometric figure that belongs to the broader category of polygons. Polygons are closed, two-dimensional shapes composed of straight lines. While it may seem like just another simple geometric shape, the heptagon presents fascinating complexities in its properties, historical uses, and real-world applications.
Brief Overview of the Article
This exploration into the world of heptagons will delve into its geometric characteristics, mathematical properties, appearances in nature and culture, and even its role in advanced mathematical theories. Whether you are a mathematician, an aspiring geometry enthusiast, or a curious reader, join us on this journey to uncover the fascinating world of heptagons.
Definition
The term “heptagon” comes from the Greek words “hepta,” which means seven, and “gonia,” which means angle. As such, a heptagon is a polygon that has seven sides and seven angles.
Every heptagon, regardless of its size or the length of its sides, shares this basic characteristic of having seven sides and seven angles. The sides are the straight lines that form the outline of the shape, and the angles are the corners where these sides meet. Each angle of a regular heptagon measures approximately 128.57 degrees, and the sum of all internal angles in any heptagon is 900 degrees.
There are two main types of heptagons: regular and irregular. A regular heptagon has all sides and angles equal. It is both cyclic (all corners lie on a single circle, known as the circumcircle) and equilateral (all sides have the same length). An irregular heptagon, on the other hand, does not have sides and angles that are all the same, and its corners do not necessarily lie on a single circle. Below is the geometric diagram of a heptagon.
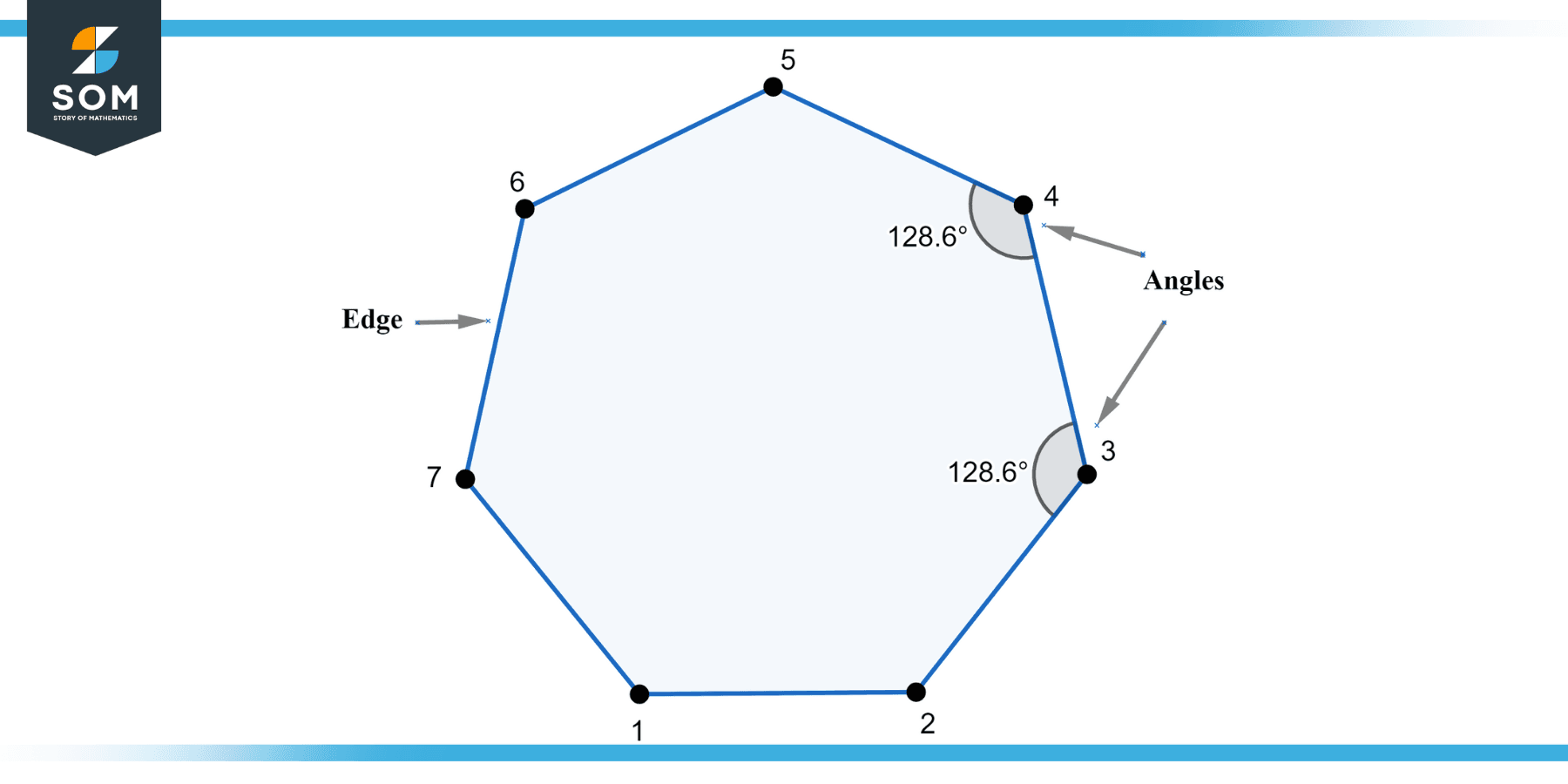
Figure-1: Heptagon.
Historical Background
Despite its relative simplicity, the heptagon has a rich historical background that illustrates the shape’s versatility and enduring fascination for mathematicians, artists, and architects alike. While the exact origins of the heptagon are difficult to trace, the study and use of heptagons can be seen throughout various cultures and periods in history.
Ancient Cultures
The ancient Greeks were among the first to study heptagons, with mathematicians like Euclid delving into the properties and construction of regular polygons. However, unlike the triangle, square, or hexagon, a regular heptagon cannot be constructed with a compass and an unmarked straightedge alone, a fact proven by Carl Friedrich Gauss in the 19th century.
Middle Ages
During the Middle Ages, the heptagon was often used in Christian symbolism. The number seven was considered sacred due to its biblical significance, and the seven-sided heptagon was used to represent the seven days of creation, the seven virtues, and the seven sacraments.
Renaissance
In the Renaissance period, artists and architects began to use heptagons in their designs. The famous Italian architect Leon Battista Alberti notably incorporated heptagonal designs into his work, recognizing the shape’s aesthetic and symbolic potential.
Modern Mathematics
In the 19th century, Carl Friedrich Gauss, a renowned German mathematician, demonstrated that a regular heptagon could be constructed using a compass, straightedge, and the ability to construct the root of a cubic equation, marking a significant development in the mathematical understanding of heptagons.
Contemporary Applications
Today, heptagons are found in various real-world applications, from the design of certain coins, such as the UK’s 50 pence and 20 pence coins, to architectural designs and even molecular structures in chemistry.
Understanding the Geometry of a Heptagon
Sides
A heptagon has seven sides. Each side is a straight line, and no two sides cross each other. In a regular heptagon, all seven sides are of equal length.
Vertices
A heptagon has seven vertices, also known as corners or points. Each vertex is the meeting point of two sides.
Angles
A heptagon has seven angles, one at each vertex. In a regular heptagon, all angles are equal, each measuring approximately 128.57 degrees. The total sum of the interior angles of any heptagon is always 900 degrees, regardless of whether it is regular or irregular.
Diagonals
A heptagon has 14 diagonals, which are line segments that connect two non-adjacent vertices.
Regular vs. Irregular Heptagons
Regular Heptagons
A regular heptagon is a polygon with seven sides of equal length and seven equal interior angles. Each angle in a regular heptagon measures approximately 128.57 degrees, and the sum of all the interior angles is 900 degrees. The regular heptagon possesses several symmetrical properties, such as rotational symmetry. It can be rotated by 51.43 degrees around its center, and it will still look the same. Additionally, a regular heptagon has reflectional symmetry along its vertical and horizontal axes, meaning it can be divided into two identical halves by these axes. Regular heptagons often appear in various contexts, including geometry, art, and architecture, due to their balanced and aesthetically pleasing shape.
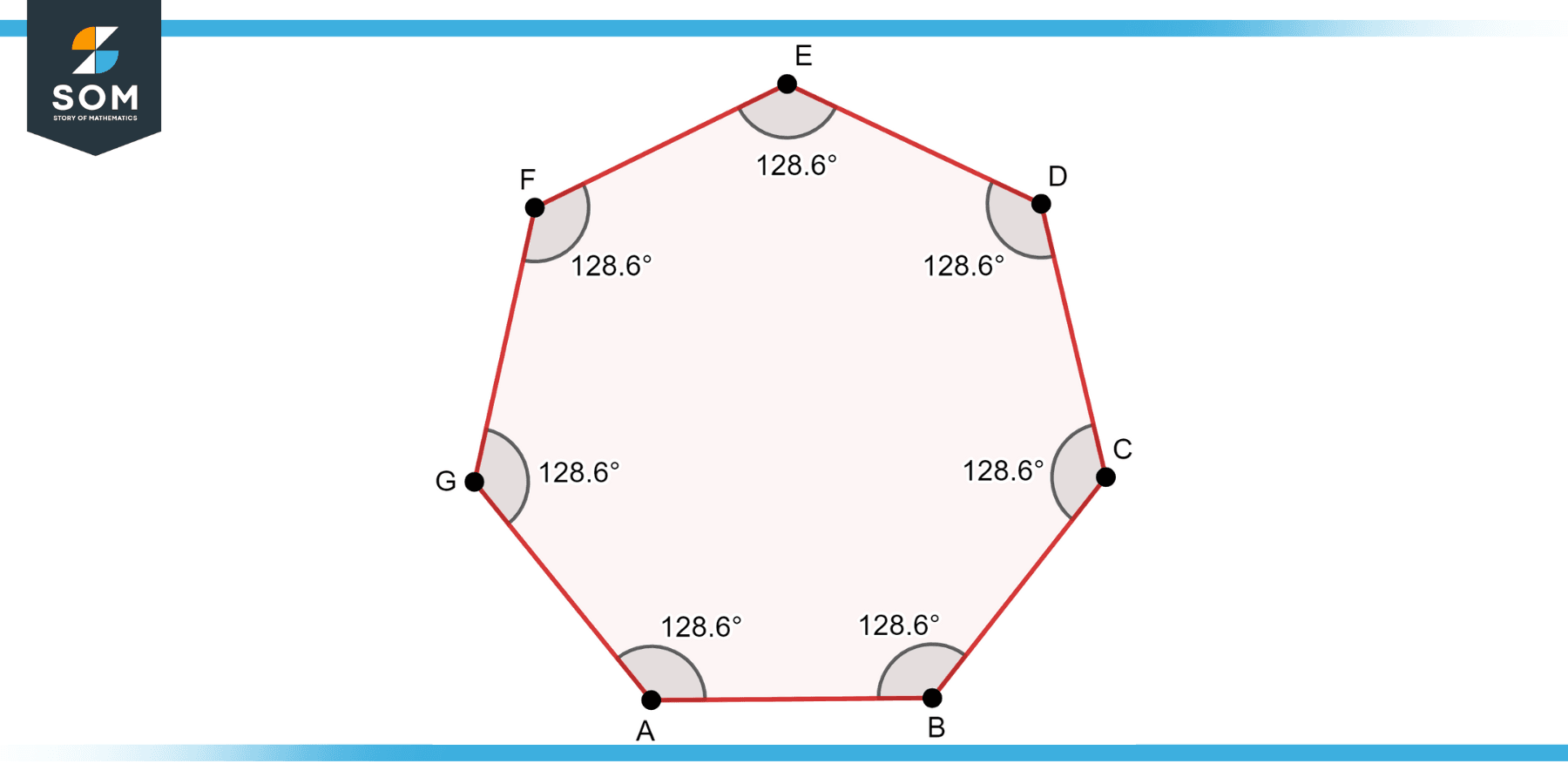
Figure-2: Regular heptagon with all interior angles of 128.6 degrees.
Irregular Heptagons
An irregular heptagon is a polygon with seven sides that are not of equal length and/or seven interior angles that are not equal. Unlike the regular heptagon, the irregular heptagon lacks symmetry and uniformity. Its angles can vary, and the lengths of its sides can differ from one another. The irregular heptagon comes in various forms, with sides and angles taking on different measurements. Its lack of symmetry gives it a more organic and unpredictable appearance compared to the regular heptagon. Irregular heptagons can be found in nature, as many organic shapes and forms exhibit irregularities, making them visually interesting and unique.
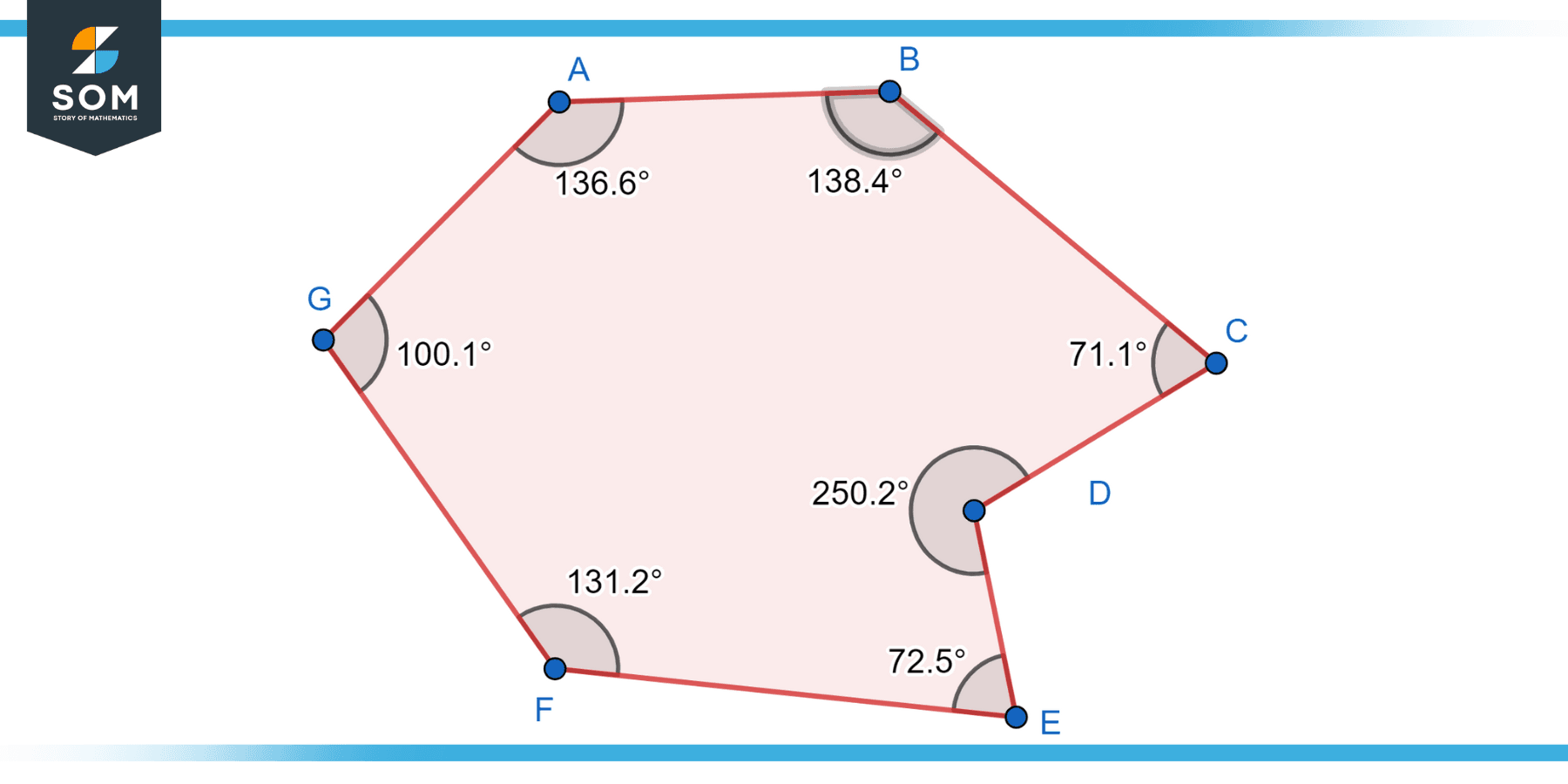
Figure-3: Irregular heptagon with different interior angles.
Circumscribed and Inscribed Circles
In a regular heptagon, a circle can be drawn that passes through all vertices (circumscribed circle), and a circle can be drawn that touches each side at its midpoint (inscribed circle). Both circles share the same center, which is also the center of the heptagon.
Symmetry
A regular heptagon has seven lines of symmetry, meaning there are seven ways you could fold the shape along a line so that both halves match exactly. Each line of symmetry runs from one vertex to the midpoint of the opposite side.
Mathematical Properties of Heptagons
A heptagon, like any polygon, has several key mathematical properties. These mathematical properties make the study of heptagons an interesting topic in the field of geometry. They are not only theoretical but also have practical applications in design, construction, and other areas of study. There are several mathematical formulas related to heptagons, particularly regular heptagons (where all sides and angles are equal). Here are some of the main ones:
The perimeter of a Regular Heptagon
The perimeter (P) is the sum of the lengths of the sides. For a regular heptagon with side length a, the perimeter is P = 7a.
Area of a Regular Heptagon
The area (A) can be calculated using the formula A = (7/4) × a² × cot(π/7), where a is the side length and cot is the cotangent function. Note that cot(π/7) is approximately 3.63391.
The sum of Interior Angles
The sum of the interior angles of a heptagon is always 900 degrees, regardless of whether it’s regular or irregular. This is calculated using the formula (n-2) × 180, where n is the number of sides.
The measure of Each Interior Angle in a Regular Heptagon
Each interior angle of a regular heptagon measures 128.57 degrees. This can be calculated using the formula [(n-2) × 180] / n, where n is the number of sides.
The measure of Each Exterior Angle in a Regular Heptagon
Each exterior angle of a regular heptagon measures 51.43 degrees. This can be calculated using the formula 360/n, where n is the number of sides.
Number of Diagonals
A heptagon has 14 diagonals. The number of diagonals in a polygon can be found using the formula n(n-3)/2, where n is the number of sides.
Radius of Circumscribed and Inscribed Circles
In a regular heptagon, the radius of the circumscribed circle (R) can be calculated as R = a / [2 × sin(π/7)], and the radius of the inscribed circle (r) can be calculated as r = a / [2 × tan(π/7)], where a is the side length, and sin and tan are the sine and tangent functions, respectively.
Heptagons in the Real World
Heptagons, while they might seem to be purely mathematical constructs, can actually be found in many places in the real world. While not as prevalent as some other geometric shapes, the heptagon nonetheless has a wide range of applications in the real world, offering a blend of practicality, aesthetics, and symbolic meaning. Below are listed some applications of heptagons:
Architecture and Design
Heptagonal shapes can be found in architectural designs and patterns, particularly in structures that use geometric shapes for aesthetic appeal. For example, heptagonal floor tiles can create unique and visually interesting patterns. The use of heptagons is not as common as simpler shapes like squares or hexagons, but they can provide a distinctive look when used in the design.
Currency
Heptagons are sometimes used in the design of coins. The UK 20-pence and 50-pence coins, for instance, are not strictly heptagonal but are equilateral curves based on the shape of a heptagon. This makes the coins easier to handle and harder to counterfeit.
Nature
Although the hexagonal pattern (such as that found in honeycombs or certain types of crystals) is more common in nature, there are instances where heptagonal patterns can occur, particularly in the plant kingdom. Some types of cacti and other succulents display a heptagonal pattern in the arrangement of their spines or leaves.
Games and Puzzles
Heptagons are used in certain board games and puzzles. For example, some strategy games use a heptagonal grid instead of the more traditional square or hexagonal grids. Heptagonal shapes can also be found in certain types of tangram puzzles.
Symbolism
In various cultures and religions, the number seven often has special significance, and this extends to the heptagon. For instance, in Christianity, the heptagon symbolizes the seven days of creation, the seven virtues, or the seven sacraments.
Mathematics and Science
Beyond the basic study of geometry, heptagons are used in more complex mathematical areas, such as graph theory and fractal geometry. In chemistry, certain molecules have a heptagonal shape, although this is less common than other shapes due to the angles involved.
Heptagons in Higher Dimensions
In higher dimensions, the concept of a heptagon extends to include polytopes, which are geometric figures with more than two dimensions. The 7-simplex, 7-cube, and 7-orthoplex (also known as a 7-cross polytope) are examples of seven-dimensional figures. However, let’s focus on two simpler examples: the heptagonal prism and the heptagonal antiprism, which are three-dimensional extensions of the heptagon.
Heptagonal Prism
This is a polyhedron with two heptagonal faces and seven rectangular faces. Imagine stretching a heptagon along a third dimension orthogonal to the plane of the heptagon to create a three-dimensional figure. This prism has 14 vertices, 21 edges, and 9 faces.
Heptagonal Antiprism
This is another polyhedron formed by two parallel heptagons connected by a ring of 14 triangles. An antiprism is similar to a prism, but the top face is rotated by an angle (usually about 180/n degrees, where n is the number of sides of the base polygon), and the lateral faces are triangles, not rectangles. The heptagonal antiprism has 14 vertices, 21 edges, and 16 faces.
In higher dimensions, such as four-dimensional space, you could also consider figures such as the heptagonal duoprism, which is the Cartesian product of two heptagons, or the heptagonal duopyramid, which is the convex hull of two heptagons in dual positions.
However, visualizing and understanding these figures requires a solid understanding of higher-dimensional geometry. In the realm of topology, a branch of mathematics that deals with properties of space that are preserved under continuous transformations, there is a seven-dimensional analog of the heptagon called a 7-hypertope. This is an example of an n-hypertope, or n-dimensional polytope.
Exercise
Example # 1
If a regular heptagon has a side length of 5 units, what is its perimeter?
Solution
The perimeter of a regular heptagon (or any polygon) is the sum of the lengths of its sides. Since a regular heptagon has sides of equal length, the perimeter can be calculated by multiplying the side length by 7 (the number of sides). So, for a side length of 5 units, the perimeter would be 5 units × 7 = 35 units.
Example # 2
If one interior angle of a regular heptagon measures 128.57 degrees, what is the sum of all the interior angles?
Solution
For a regular heptagon, all interior angles are equal. Since there are seven angles in a heptagon, the sum of all the interior angles would be 128.57 degrees × 7 = 900 degrees.
Example # 3
Calculate the measure of each exterior angle in a regular heptagon.
Solution
The sum of the exterior angles for any polygon is always 360 degrees. For a regular heptagon, all exterior angles are equal so that each exterior angle would measure 360 degrees / 7 = 51.43 degrees.
Example # 4
Calculate the area for the heptagon given in Figure-4.
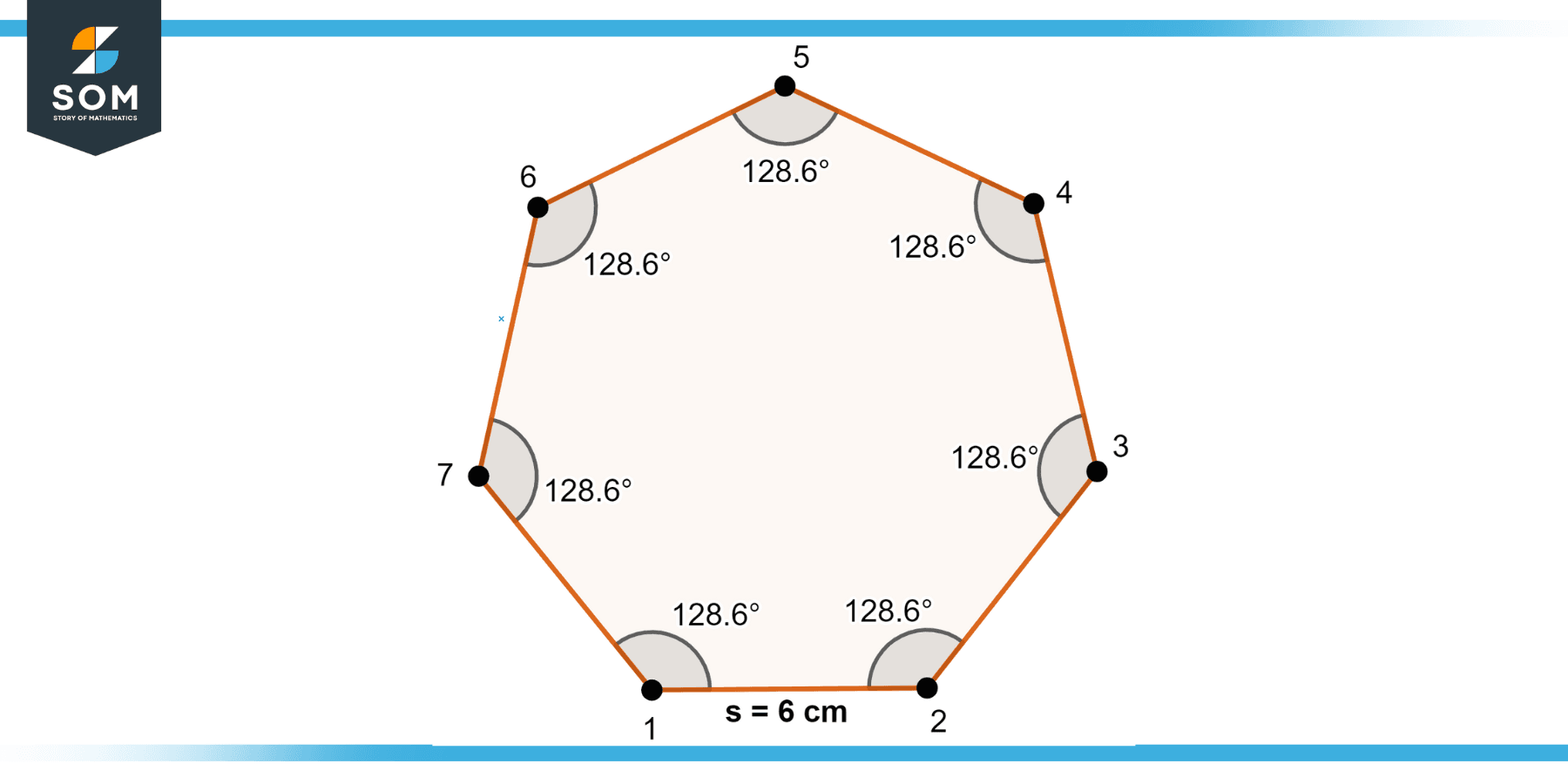
Figure-4
Solution
The area A of a regular heptagon can be calculated using the formula: A = (7/4) × a² × cot(π/7), where a is the side length and cot is the cotangent function. Using this formula with a side length of 6 cm and knowing that cot(π/7) is approximately 3.63391, the area is A = (7/4) * (6 cm)² × 3.63391 ≈ 116.26 cm².
Example # 5
Find the length of the side of a regular heptagon if its area is 200 square units.
Solution
You can use the formula for the area of a regular heptagon, which is A = (7/4) × a² × cot(π/7), where A is the area and a is the side length. Solving for a, we get $a = \sqrt{\frac{A}{[(7/4) × cot(π/7)]}}$. Given that the area is 200 square units and cot(π/7) is approximately 3.63391, we substitute these values into the equation to get $a = \sqrt{\frac{A}{[(7/4) × cot(π/7)]}}$ ≈ 7.39 units.
Example # 6
If the radius of the inscribed circle (inradius) of a regular heptagon is 5 units, what is the length of each side?
Solution
The length of the side (a) of a regular heptagon with an inradius (r) can be calculated using the formula a = 2r × tan(π/7), where tan is the tangent function. Substituting the given value of r = 5 units into the equation and knowing that tan(π/7) is approximately 0.40403, we get a = 2 × 5 units × 0.40403 ≈ 4.04 units.
Example # 7
Calculate the radius of the circumscribed circle (circumradius) of a regular heptagon with a side length of 8 units.
Solution
The circumradius (R) of a regular heptagon can be calculated using the formula R = a / [2 × sin(π/7)], where a is the side length, and sin is the sine function. Substituting the given value of a = 8 units into the equation and knowing that sin(π/7) is approximately 0.43388, we get R = 8 units / [2 × 0.43388] ≈ 9.23 units.
Example # 8
Find the area and perimeter of a regular heptagon whose side is 5 cm?
Solution
Given:
The side of a heptagon, a = 5 cm
We know that, the area of a heptagon, A = (7/4) × a² × cot(π/7) square units
Substitute a = 5 cm in the formula,
A = (7/4) × 5² × cot(π/7)
A = 3.634× 5²
A = 90.85 cm²
Therefore, the area of a heptagon is 90.85 cm2
The perimeter of a heptagon, P = 7a units
P = 7(5)
P = 35 cm
Hence, the perimeter of a heptagon is 35 cm.
All images were created with GeoGebra.
