Parametric Vector Form – Definition and Examples

In the vast expanse of mathematical vectors, the ‘parametric vector form’ stands as a beacon, illuminating complex geometric and algebraic problems with precision and clarity. This form, often an unsung hero, enables mathematicians and physicists alike to define lines and curves in space more efficiently than traditional methods.

Dive into this article as we unravel the intricacies of this mathematical concept, exploring its foundational principles and its increasing relevance in today’s digital realm.

Definition of Parametric Vector Form

The parametric vector form is a method of representing geometric entities, like lines and curves, using vectors and parameters. This form is particularly useful in three-dimensional spaces but is applicable to two-dimensional spaces as well.

For a line in space, the parametric vector form is given by:

$\mathbf{r}(t)=\mathbf{a}+t\mathbf{b}$

Where:

• $\mathbf{r}(t)$ is the position vector of a generic point on the line as a function of the parameter $t$.
• $\mathbf{a}$ is the position vector of a specific point on the line (often referred to as the ‘anchor’ point).
• $\mathbf{b}$ is a direction vector along the line (not necessarily of unit length).
• $t$ is a scalar parameter. As $t$ varies, the point $\mathbf{r}(t)$ traces the line in the direction of $\mathbf{b}$.

This representation is advantageous because it captures both the position and direction of a line using vectors. The parameter $t$ allows us to determine any point on the line, making this form particularly useful in physics and engineering where we often want to trace the path of an object or determine its position at various times.

It’s important to note that for curves (which may not be straight lines), the parametric form can be more complex, involving different functions for each component of the vector $\mathbf{r}(t)$.

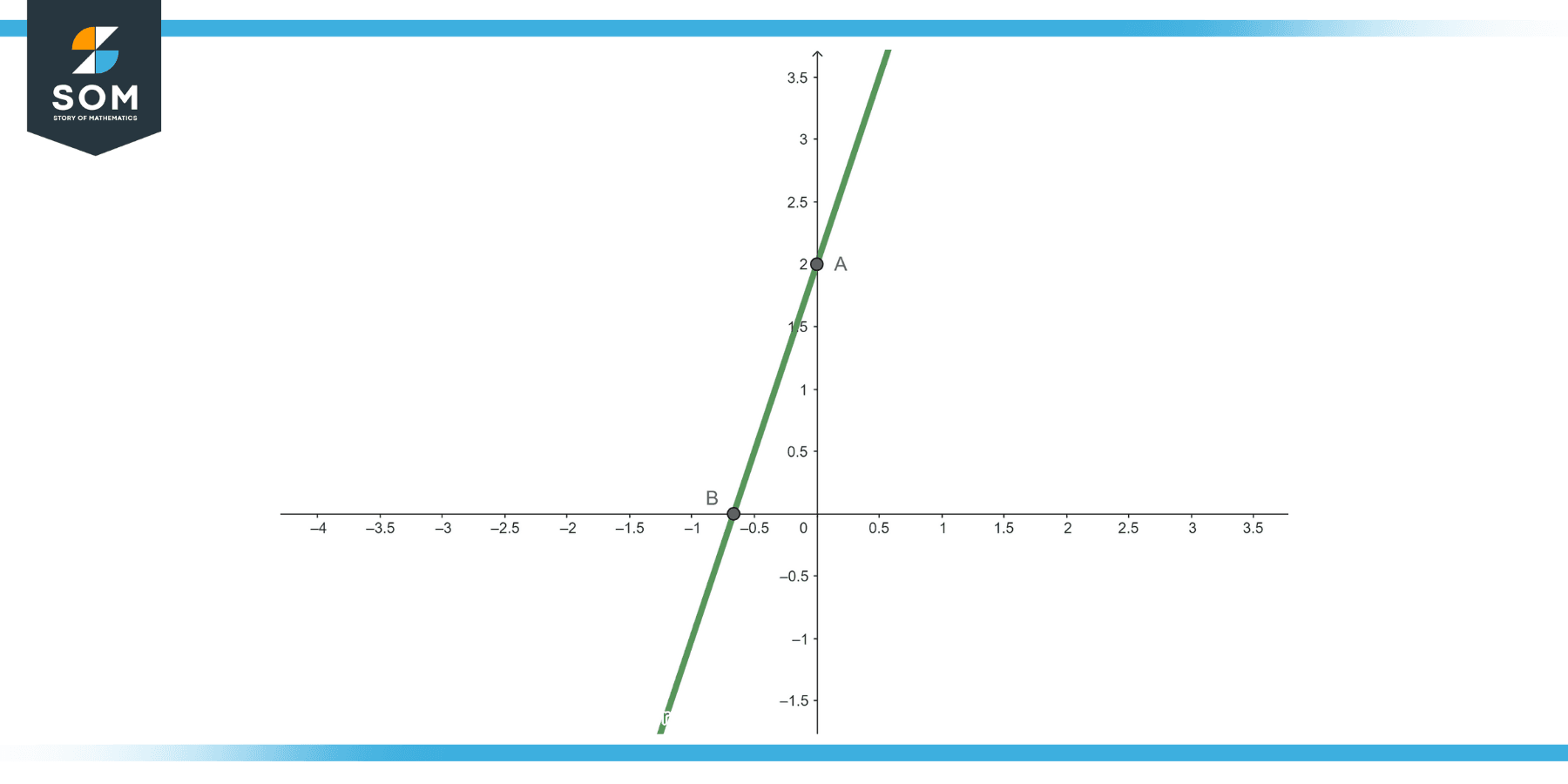
Figure-1.

Properties of Parametric Vector Form

The parametric vector form, most commonly used to represent lines in space, offers a compact and efficient means to depict linear motion or the position of points on a straight path. Let’s delve deep into its properties to fully understand its implications:

The Uniqueness of Representation (With Caveats)

For a given line in space, its parametric vector form is unique if you fix a particular point on the line (the anchor point) and a specific direction vector. However, it’s worth noting that there are infinitely many representations for the same line. This is because you can choose any point on the line as your anchor and any scalar multiple of a given direction vector to represent the same line.

The Flexibility of the Parameter $t$

The parameter $t$ can take any real value, from negative infinity to positive infinity. When $t=0$, the position vector $\mathbf{r}(t)$ coincides with the anchor vector $\mathbf{a}$. As $t$ increases or decreases, you move along the line in the direction of $\mathbf{b}$ or opposite to it, respectively.

Continuous Motion and Tracing

The parametric form describes continuous motion along a line. As $t$ varies, the end of the vector $\mathbf{r}(t)$ traces the entire line. This property makes the form particularly useful in physics for modeling objects’ paths or in computer graphics for drawing or rendering linear paths.

Directionality

The direction vector $\mathbf{b}$ is crucial. It not only determines the direction of the line but also the “speed” at which the line is traced as $t$ varies. For a unit direction vector, a unit change in $t$ represents a unit movement along the line. However, for a non-unit direction vector, the rate of movement along the line is proportional to the magnitude of $\mathbf{b}$.

Scalability of the Direction Vector

Any scalar multiple of the direction vector $\mathbf{b}$ will represent the same line in space, though the rate of traversal might differ. For instance, if you double the magnitude of $\mathbf{b}$, you’ll move twice as fast along the line for the same change in $t$.

Collinearity Test

Two points are collinear with the anchor point if their position vectors satisfy the parametric equation of the line. This is a handy property when you want to check if three or more points lie on the same straight line.

Limitations for Curves

While the parametric vector form can represent any straight line in space uniquely (with a chosen anchor and direction), it becomes more intricate for curves. Curves might need a different function for each component of the position vector, making them more challenging to work with in this form.

Intersection and Parallelism

Using the parametric vector form, one can quickly determine if two lines intersect or are parallel. If their direction vectors are scalar multiples of one another, the lines are either parallel or coincident. Otherwise, you can equate the two parametric equations to find a common point for intersection.

Exercise 

Example 1

Find the parametric vector form of a line passing through the point $A(1,2,3)$ and parallel to the vector $\mathbf{b}=⟨2,3,1⟩$.

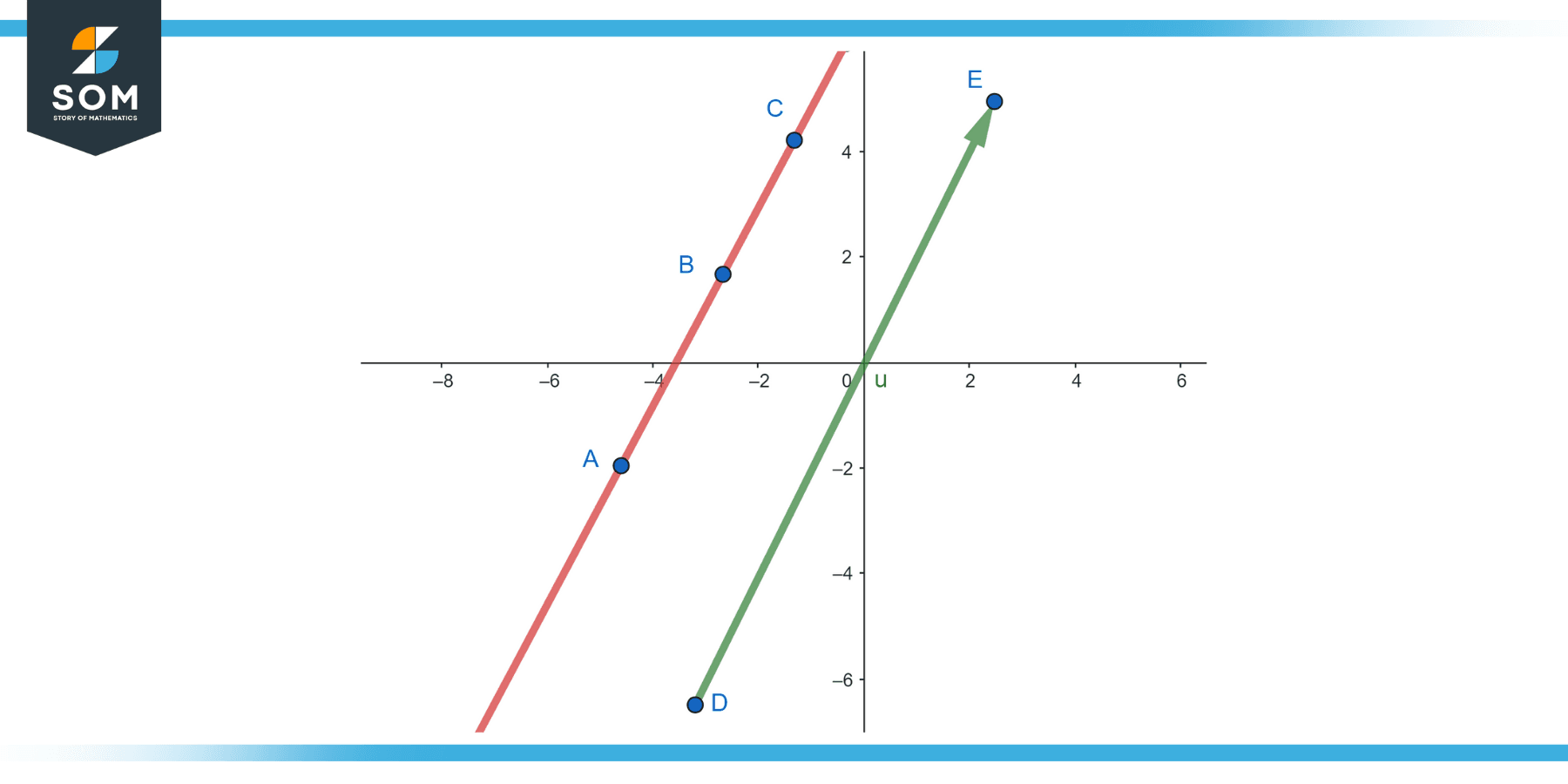
Figure-2.

Solution

Using the formula $\mathbf{r}(t)=\mathbf{a}+t\mathbf{b}$:

$\mathbf{r}(t)=⟨1,2,3⟩+t⟨2,3,1⟩$

$\mathbf{r}(t)=⟨1+2t,2+3t,3+t⟩$

Example 2

For the line $\mathbf{r}(t)=⟨1+t,4-2t,3t⟩$, find the point on the line when $t=2$.

Solution

Substitute $t=2$ into the equation:

$\mathbf{r}(2)=⟨1+2,4-4,6⟩=⟨3,0,6⟩$

Example 3

Determine if the point $P(3,0,6)$ lies on the line $\mathbf{r}(t)=⟨1+t,4-2t,3t⟩$.

Solution

From Example 2, we already found that for $t=2$, the point on the line is $P(3,0,6)$. Hence, point P lies on the line.

Example 4

For the line $\mathbf{r}(t)=⟨2+3t,1-t,4t⟩$, determine the point on the line for $t=0$.

Solution

Substitute $t=0$ into the equation:

$\mathbf{r}(0)=⟨2,1,0⟩$

Example 5

Find the parametric vector form of a line passing through $A(1,2,3)$ and perpendicular to the vector $\mathbf{c}=⟨3,2,1⟩$.

Solution

The direction vector of the line is the cross product of the position vector of point A and vector $\mathbf{c}$. But for simplicity, let’s consider the line’s direction vector to be $\mathbf{c}$ itself.

So, the line is:

$\mathbf{r}(t)=⟨1,2,3⟩+t⟨3,2,1⟩$

$\mathbf{r}(t)=⟨1+3t,2+2t,3+t⟩$

All images were created with GeoGebra.