
In mathematics, few concepts possess the real number system‘s captivating power and profound significance. From the enchanting elegance of whole numbers to the mystifying infinitude of decimals, the real number system is the bedrock upon which mathematical analysis is built.
While we may encounter real numbers daily, their true nature and remarkable properties often remain concealed beneath the surface. In this article, we embark on a journey of discovery to demystify the real number system, unravel its intricacies, and appreciate its boundless wonders.
So, fasten your intellectual seatbelts and prepare to explore the captivating universe of real numbers.
Defining Real Number System
The real number system is a fundamental mathematical construct encompassing the set of all possible numbers, rational and irrational, and serves as the foundation for mathematical analysis.
Real numbers are characterized by their ability to represent quantities on a continuous number line, where each point corresponds to a unique real number.
The real number system includes familiar entities such as whole numbers, integers, fractions, decimals, less intuitive numbers like square roots, transcendental numbers (e.g., π and e), and even non-repeating decimals.
This expansive collection of numbers exhibits crucial properties, such as closure under addition, subtraction, multiplication, and division, enabling intricate mathematical investigations and providing a framework for modeling and understanding the physical world.
Figure-1.
Properties of Real Number System
The real number system possesses several key properties that define its nature and make it a fundamental mathematical construct. Let’s delve into these properties in detail:
Closure Property
The real number system is closed under addition and multiplication. This means that when you add or multiply two real numbers, there is always another real number. For example, if a and b are real numbers, then a + b and a * b are real numbers.
Commutative Property
The operations of addition and multiplication are commutative in the real number system. This means that changing the order of the numbers added or multiplied does not affect the result.
For instance, for real numbers a and b, a + b = b + a and a * b = b * a. The commutative property allows for flexibility in rearranging terms without altering the outcome of the operation.
Associative Property
Addition and multiplication in the real number system are associative operations. This means that the grouping of added or multiplied numbers does not affect the result.
For any real numbers a, b, and c, (a + b) + c = a + (b + c) and (a * b) * c = a * (b * c). The associative property ensures that the order in which operations are performed does not change the outcome.
Distributive Property
The real number system obeys the distributive property, which relates addition and multiplication. For real numbers a, b, and c, the distributive property states that a * (b + c) = a * b + a * c.
Identity Elements
The real number system possesses two identity elements – one for addition and multiplication. The additive identity is 0, which means that for any real number a, a + 0 = 0 + a = a. The multiplicative identity is 1, so for any real number a, a * 1 = 1 * a = a.
Inverse Elements
Every non-zero real number has an additive inverse and a multiplicative inverse. The additive inverse of a real number a is denoted as -a and satisfies the property a + (-a) = (-a) + a = 0. The multiplicative inverse of a non-zero real number a is denoted as 1/a or a^(-1) and satisfies the property a * (1/a) = (1/a) * a = 1.
Ordering Property
The real number system is equipped with an ordering relation, which allows us to compare and arrange real numbers in ascending or descending order. This property is known as the trichotomy law. For any two real numbers, a and b, exactly one of the following holds: a < b (a is less than b), a > b (a is greater than b), or a = b (a is equal to b).
Density Property
The real number system exhibits the density property, which states that between any two distinct real numbers, there exists another real number. This implies that there are infinitely many real numbers between any two given real numbers, making the real number line densely populated.
Completeness Property
The real number system possesses the completeness property, the Dedekind completeness, or the least upper bound property. This property guarantees that every non-empty set of real numbers bounded above has a least upper bound (supremum) in the real number system. It ensures no “gaps” or “holes” in the real number line, allowing for precise mathematical analysis and continuity.
Applications
The real number system finds applications in various fields and disciplines as a fundamental mathematical construct. Here are some examples of how the real number system is applied in different fields:
Physics and Engineering
The real number system is essential for modeling and analyzing physical phenomena in physics and engineering. Real numbers represent distance, time, temperature, energy, and more. The principles of calculus, which heavily rely on real numbers, are employed to describe and predict the behavior of physical systems.
Economics and Finance
Real numbers are extensively used in economics and finance to represent quantities such as prices, quantities of goods and services, interest rates, investments, and monetary values. Concepts like supply and demand, market equilibrium, and financial calculations rely on real numbers for accurate analysis and decision-making.
Computer Science and Information Technology
In computer science and information technology, real numbers are employed for numerical computations, algorithms, simulations, and data analysis. Real numbers represent and process continuous data, such as sensor measurements, image and signal processing, and scientific simulations.
Statistics and Data Analysis
Real numbers play a crucial role in statistics and data analysis, where they are used to represent numerical data, measure variability, calculate averages, and perform statistical tests. Real numbers enable the interpretation and communication of quantitative information derived from data.
Architecture and Design
The real number system is utilized in architecture and design to express and work with measurements, dimensions, proportions, and spatial relationships. Architects and designers rely on real numbers to ensure accuracy and precision in creating buildings, structures, and artistic compositions.
Medicine and Biotechnology
Real numbers are applied in medicine and biotechnology for medical measurements, data analysis, drug dosage calculations, and modeling physiological processes. Real numbers enable accurate representation and interpretation of biological and medical data, facilitating diagnoses, treatment plans, and research.
Geographic Information Systems (GIS)
GIS systems extensively utilize real numbers for representing spatial coordinates, distances, elevations, and other geographic attributes. Real numbers enable precise mapping, navigation, location-based services, and spatial analysis.
Cryptography and Cybersecurity
Real numbers are involved in cryptographic algorithms, which provide secure communication and data protection. Real numbers play a role in mathematical operations used in encryption, decryption, digital signatures, and secure key generation.
Probability Theory and Risk Analysis
Real numbers are employed in probability theory and risk analysis to quantify uncertainties and assess probabilities. Real numbers enable the formulation of probability distributions, risk models, and statistical measures used in decision-making and risk management.
Exercise
Example 1
Simplify the expression: √(9 + √16)
Solution
We start by simplifying the expression inside the square root:
= √(9 + √16)
= √(9 + 4)
= √13
The simplified expression is √13.
Example 2
Solve the equation: |2x – 3| = 7
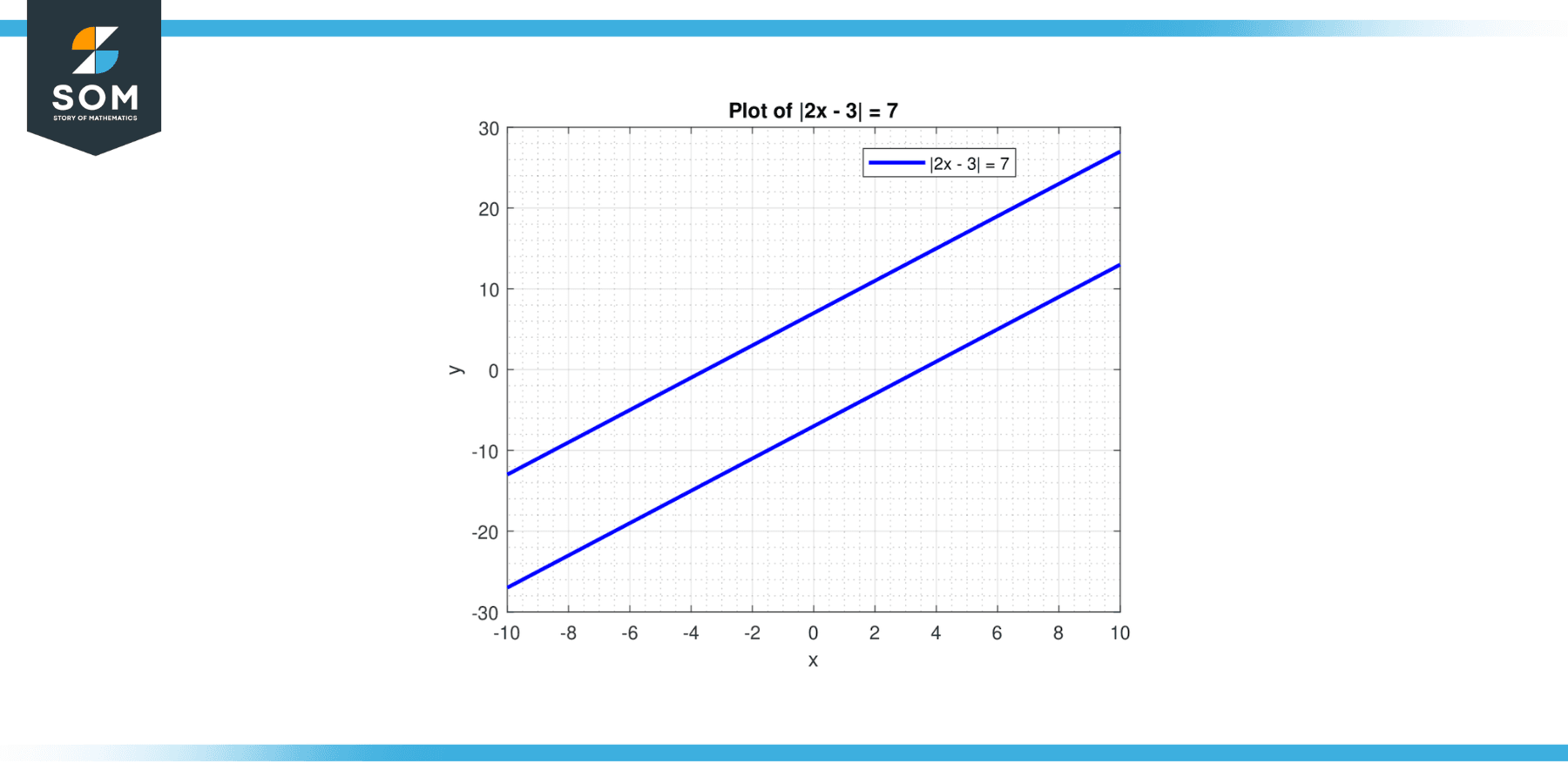
Figure-2.
Solution
We consider two cases: when 2x – 3 is positive and negative.
Case 1: 2x – 3 > 0
In this case, 2x – 3 = 7. Adding 3 to both sides, we get 2x = 10. Dividing by 2, we find x = 5.
Case 2: 2x – 3 < 0
In this case, we have -(2x – 3) = 7. Expanding the negative sign, we get -2x + 3 = 7. Subtracting 3 from both sides, we have -2x = 4. Dividing by -2, we find x = -2.
The solutions to the equation |2x – 3| = 7 are: x = 5 and x = -2.
Example 3
Find the domain of the function f(x) = √(5 – x).
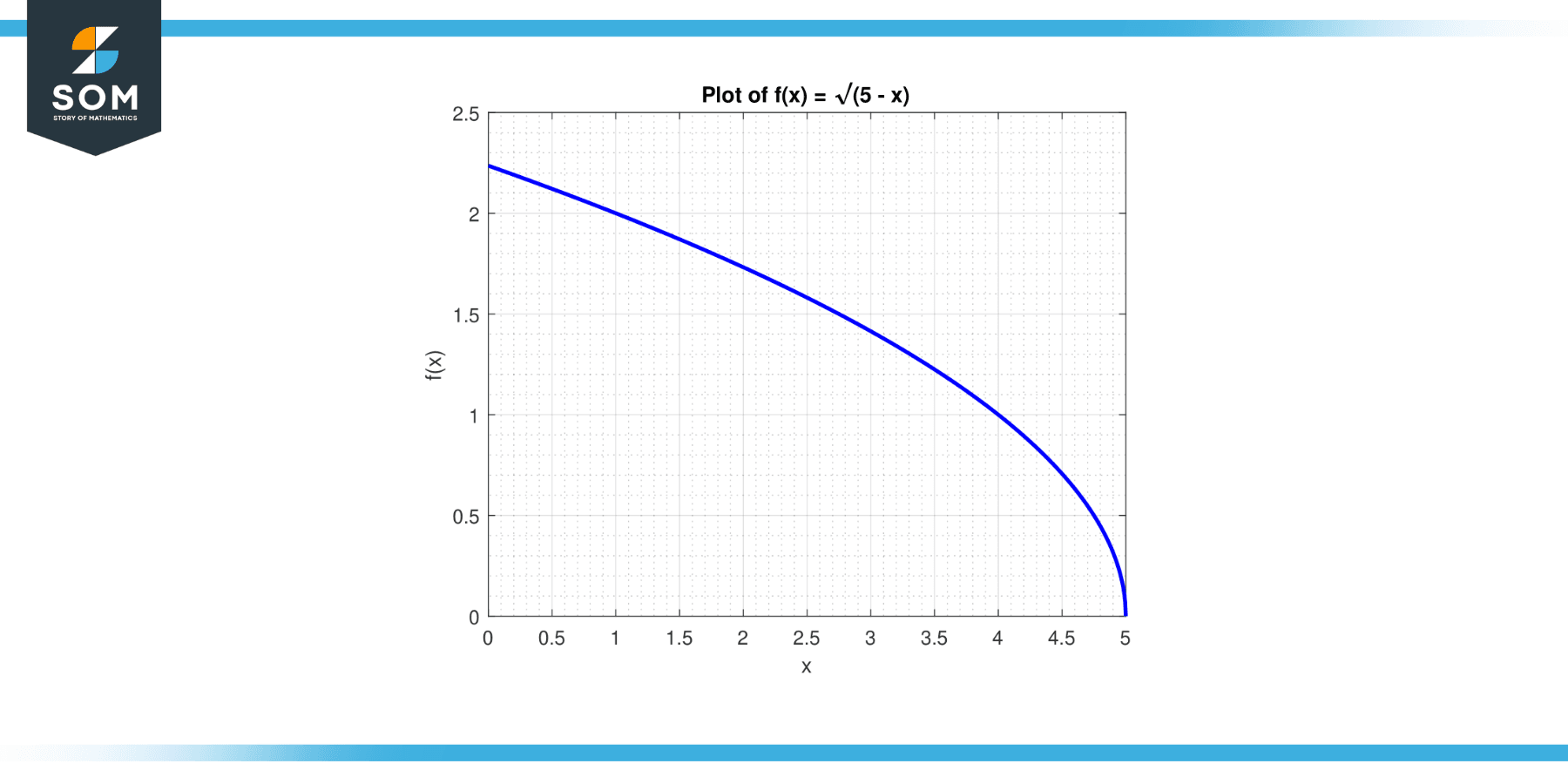
Figure-3.
Solution
The domain of a function is the set of all possible values of x for which the function is defined. In this case, the square root function is defined for non-negative real numbers.
Therefore, the expression inside the square root must be non-negative:
5 – x ≥ 0
Solving the inequality, we find:
x ≤ 5.
The domain of the function f(x) = √(5 – x) is x ≤ 5.
Example 4
Evaluate the expression: log₁₀(1000)
Solution
The logarithm functions log₁₀(x) gives the power to which 10 must be raised to obtain x. In this case, we have log₁₀(1000)= 3 since 10³ = 1000.
The value of log₁₀(1000) is 3.
Example 5
Solve the inequality: 2x – 5 > 3x + 1
Solution
To solve the inequality, we need to isolate x on one side.
2x – 5 > 3x + 1
Subtracting 2x from both sides, we get:
-5 > x + 1
Subtracting 1 from both sides, we have:
-6 > x
The solution to the inequality 2x – 5 > 3x + 1 is x < -6.
Example 6
Find the absolute value of -8.
Solution
The absolute value of a real number is its distance from zero on the number line. The absolute value of -8 is 8, as -8 is 8 units away from zero in the negative direction.
The absolute value of -8 is 8.
Example 7
Find the decimal representation of the fraction 3/5.
Solution
To find the decimal representation of the fraction 3/5, we divide 3 by 5.
3 ÷ 5 = 0.6
The decimal representation of the fraction 3/5 is 0.6.
Example 8
Solve the equation: 2x² – 5x + 2 = 0.
Solution
We can solve this quadratic equation by factoring, completing the square, or using the quadratic formula.
Using factoring: The equation factors as (2x – 1)(x – 2) = 0. Setting each factor equal to zero, we have two possibilities:
2x – 1 = 0
which gives:
x = 1/2
x – 2 = 0
which gives
x = 2
The solutions to the equation 2x² – 5x + 2 = 0 are x = 1/2 and x = 2.
