JUMP TO TOPIC

The volume of a parallelepiped serves as an intriguing point of exploration, while embarking on a journey into the realm of three-dimensional space.
As a polyhedron enveloped by six parallelograms, a parallelepiped is a geometric marvel that offers rich insights into the interplay of vectors and spatial dimensions.
This article aims to unfold the intricacies of parallelepipeds, diving into the concept, its intriguing properties, and the mathematical elegance of its volume calculation.
Strap in as we traverse the vibrant landscape of parallelepipeds, delving into a world where geometry coalesces with algebra, illuminating corners of mathematical understanding with fascinating clarity.
Defining the Volume of a Parallelepiped
The volume of a parallelepiped is the measure of the three-dimensional space it encompasses or occupies. In terms of vectors, if a parallelepiped is formed by three vectors a, b, and c, in three-dimensional space starting from the same point, the volume is calculated using the scalar triple product of these vectors.
Mathematically, this is represented as the absolute value of the dot product of vector a and the cross product of vectors b and c, denoted as V = |a . (b x c)|. This volume calculation is a reflection of the parallelepiped’s spatial properties, taking into account the lengths of its edges and the angles between them.
Below in figure-1, we present a generic diagram for a parallelepiped with its volume.
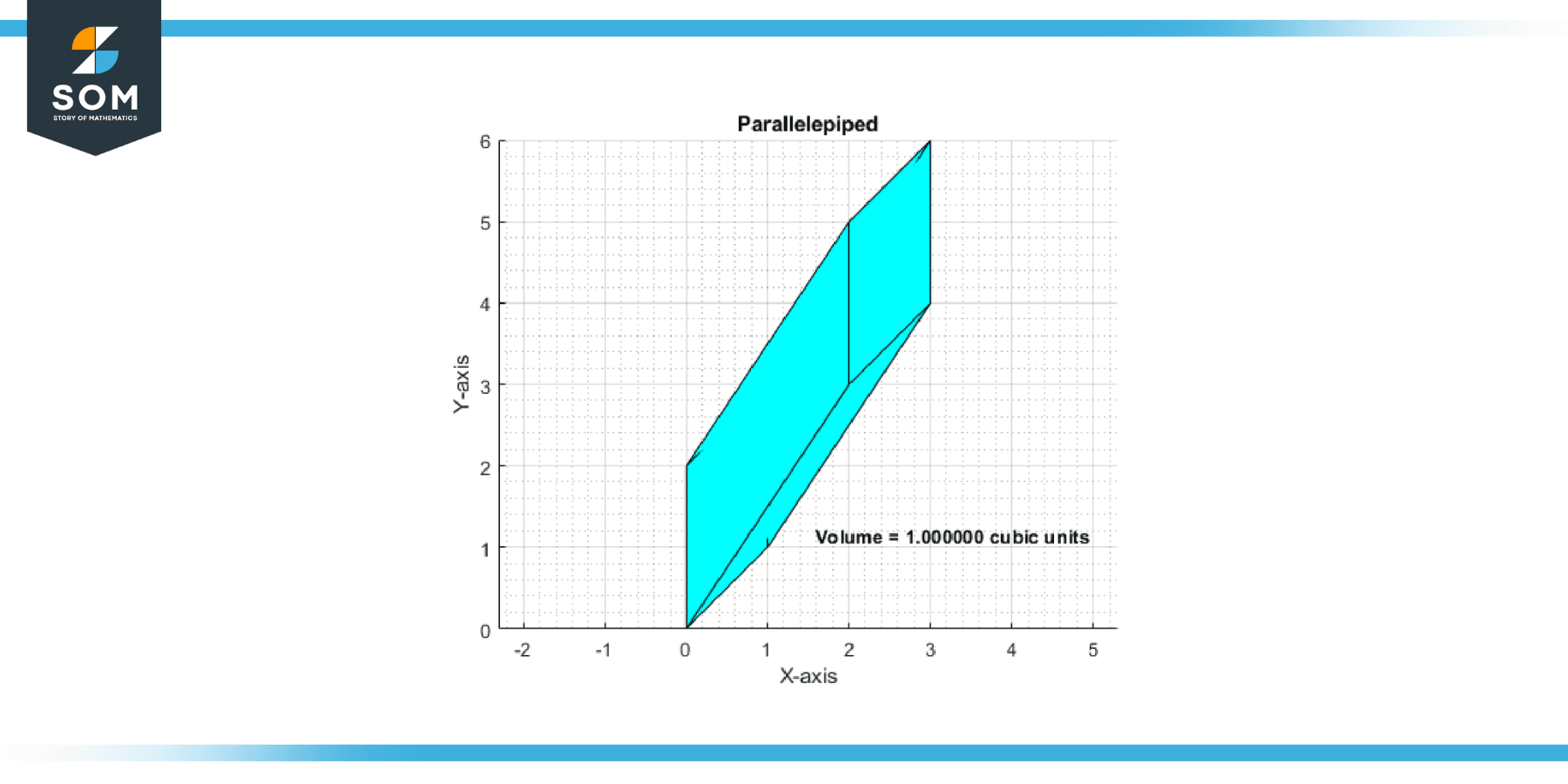
Figure-1.
Computing the Volume of a Parallelepiped
The volume (V) of a parallelepiped can be found using the scalar triple product of the three vectors defining the edges of the parallelepiped. If vectors a, b, and c form the edges of the parallelepiped, the volume is given by:
V = | a . (b x c) |
Where:
- “.” denotes the dot product of two vectors.
- “x” denotes the cross product of two vectors.
- “|” around the expression denotes the absolute value.
The scalar triple product is equivalent to the determinant of a 3×3 matrix with the components of vectors a, b, and c as its rows or columns:
V = | det([a; b; c]) |
It’s important to note that the volume of a parallelepiped is always positive, so the absolute value operation ensures this.
Properties
The volume of a parallelepiped, a three-dimensional geometric entity characterized by six parallelogram faces, has several mathematical and geometrical defining properties. Understanding these properties can provide a profound insight into three-dimensional space and its geometric manifestations.
Defined by Scalar Triple Product
One of the central properties of the volume of a parallelepiped is that it is given by the scalar triple product of three vectors a, b, and c that define the edges of the parallelepiped. The scalar triple product of a, b, and c is calculated as the absolute value of vector a’s dot product and the cross product of vectors b and c, denoted as V = |a . (b x c)|.
Non-negative Quantity
The volume of a parallelepiped is always a non-negative quantity. This is because it represents a physical quantity, the amount of space occupied by the parallelepiped, which cannot be negative. The scalar triple product’s absolute value ensures the volume’s non-negativity.
Zero Volume Implies Coplanar Vectors
If the volume of a parallelepiped is zero, it implies that the three vectors defining the edges of the parallelepiped are coplanar, i.e., they lie in the same plane. This is because the volume, computed as the scalar triple product, will be zero if the vectors are coplanar, as the height of the parallelepiped would be zero in such a case.
Invariant under Permutations of Vectors
The volume of the parallelepiped remains the same even if the order of the vectors a, b, and c in the scalar triple product is permuted cyclically, i.e., V = |b . (c x a)| = |c . (a x b)|. This is because the cyclic permutation of the vectors does not change the physical configuration of the parallelepiped.
Change of Sign Under Anti-cyclic Permutations
The volume changes sign under an anti-cyclic permutation of the vectors a, b, and c, i.e., V = – |a . (c x b)|. Although the volume itself, being an absolute value, is always non-negative, the scalar triple product can be negative, reflecting the vectors’ orientation.
Dependence on Edge Lengths and Angles
The parallelepiped volume depends on the edges’ lengths and the angles between them. More specifically, it’s the product of the areas of the base (given by the magnitude of the cross product of vectors b and c) and the height (given by the projection of a vector a onto the vector perpendicular to the base).
Connection to Determinants
The scalar triple product that gives the volume of a parallelepiped can also be viewed as the determinant of a 3×3 matrix whose rows or columns are the components of the vectors a, b, and c. This links the volume of a parallelepiped and the determinant concept in linear algebra.
Applications
Mathematics
In mathematics, the volume of a parallelepiped is an important concept in three-dimensional geometry. It is used to calculate the volume of irregularly shaped objects and is a key component in the study of solid geometry.
Physics
In physics, the volume of a parallelepiped is used to calculate the volume of three-dimensional objects, such as containers, tanks, or any other physical systems with a parallelepiped shape. It is an essential parameter in various physical calculations involving mass, density, fluid flow, and material properties.
Engineering
In engineering disciplines, the volume of a parallelepiped is crucial for determining the capacity, flow rate, and storage requirements of containers, pipes, and channels. It is also used in structural analysis to calculate solid objects’ displacement, stress, and strain.
Architecture
In architecture, the volume of a parallelepiped is used to measure the enclosed space within a building or room. It is essential for determining room dimensions, and material quantities, and estimating costs. Additionally, it plays a role in designing efficient ventilation and heating/cooling systems.
Computer Graphics and Animation
In computer graphics and animation, the volume of a parallelepiped is used to define the boundaries and physical characteristics of 3D objects. It is vital for creating realistic simulations, rendering scenes, and modeling complex shapes in virtual environments.
Manufacturing and Material Science
In manufacturing processes, the volume of a parallelepiped is used to calculate material requirements, determine material utilization rates, and estimate production costs. It is also relevant in material science for analyzing properties such as density, porosity, and elasticity.
Fluid Dynamics
In fluid dynamics, the volume of a parallelepiped is used to calculate the volume of fluid displaced by an object immersed in a fluid. This information is crucial for understanding buoyancy forces, hydrostatic pressure, and fluid flow characteristics.
Exercise
Example 1
Given vectors a = [2, 3, 4], b = [1, 1, 1], and c = [0, 2, 3], calculate the volume of the parallelepiped spanned by these vectors.
Solution
The volume V of a parallelepiped can be found using the scalar triple product of the three vectors. So:
V = |a . (b x c)|
First, we calculate the cross product of vectors b and c:
b x c = [(1)(3) – (1)(2), (1)(0) – (1)(3), (1)(2) – (1)(0)]
b x c = [1, -3, 2]
Then, calculate the dot product of vector a and the result:
a . (b x c) = (2)(1) + (3)(-3) + (4)(2)
a . (b x c) = 2 – 9 + 8
a . (b x c) = 1
Taking the absolute value gives us the volume of the parallelepiped:
V = |1| = 1
Example 2
Given vectors a = [4, 1, -1], b = [2, 0, 2], and c = [1, 1, 1], find the volume of the parallelepiped spanned by these vectors.
Solution
Calculate the volume using the scalar triple product:
V = |a . (b x c)|
First, find the cross product b x c:
b x c = [(0)(1) – (2)(1), (2)(1) – (2)(1), (2)(1) – (0)(0)]
b x c = [-2, 0, 2]
Then, calculate the dot product with vector a:
a . (b x c) = (4)(-2) + (1)(0) + (-1)(2)
a . (b x c) = -8 – 2
a . (b x c) = -10
The volume of the parallelepiped is the absolute value of this result:
V = |-10| = 10
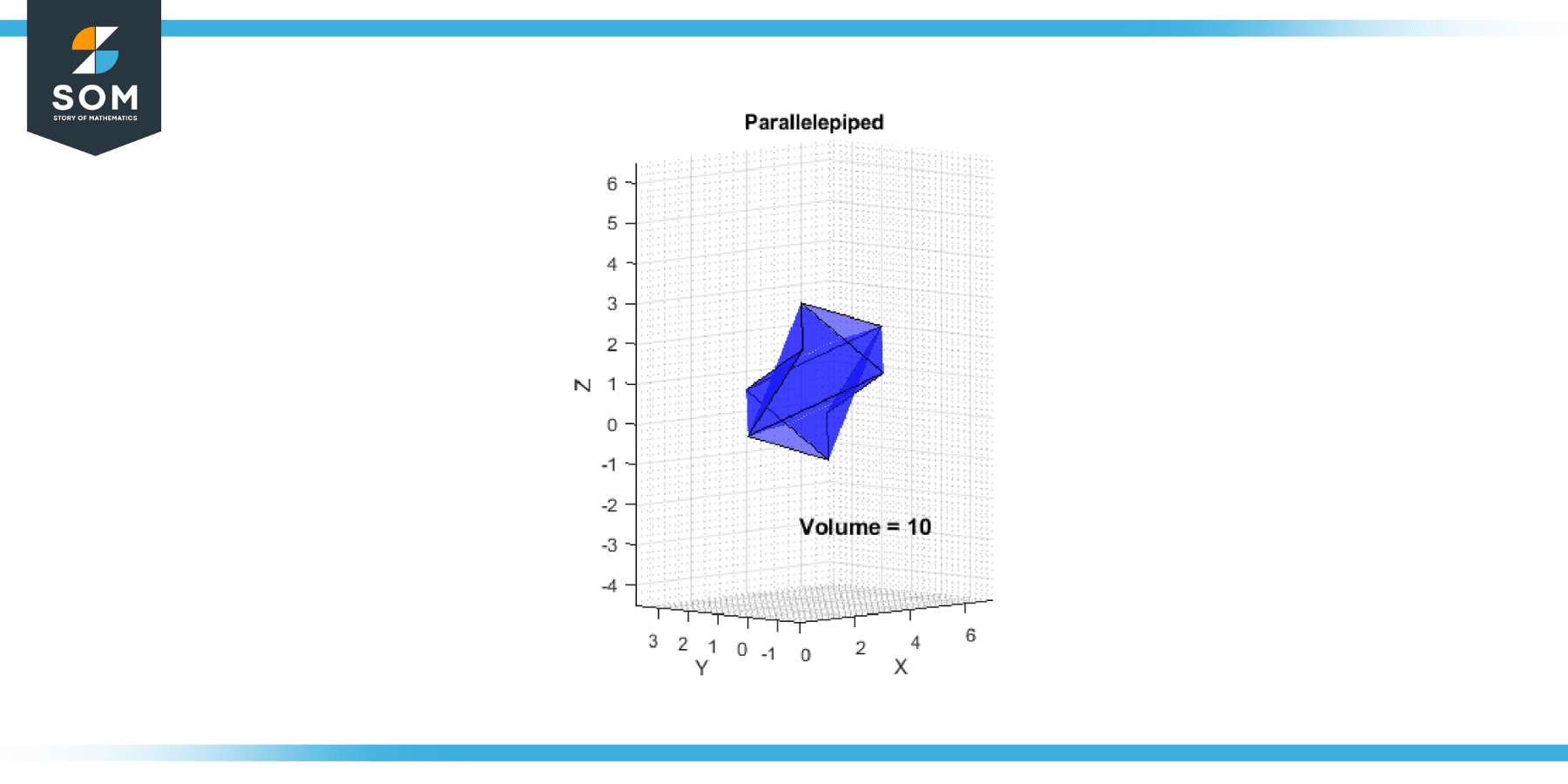
Figure-2.
Example 3
Given vectors a = [3, 0, 0], b = [0, 3, 0], and c = [0, 0, 3], calculate the volume of the parallelepiped spanned by these vectors.
Solution
Calculate the volume using the scalar triple product:
V = |a . (b x c)|
First, calculate the cross product b x c:
b x c = [(0)(3) – (0)(3), (3)(0) – (0)(3), (0)(3) – (0)(0)]
b x c = [0, 0, 9]
The dot product of vector a and the result is then:
a . (b x c) = (3)(0) + (0)(0) + (0)(9)
a . (b x c) = 0
So, the volume of the parallelepiped is:
V = |0| = 0
The vectors are coplanar.
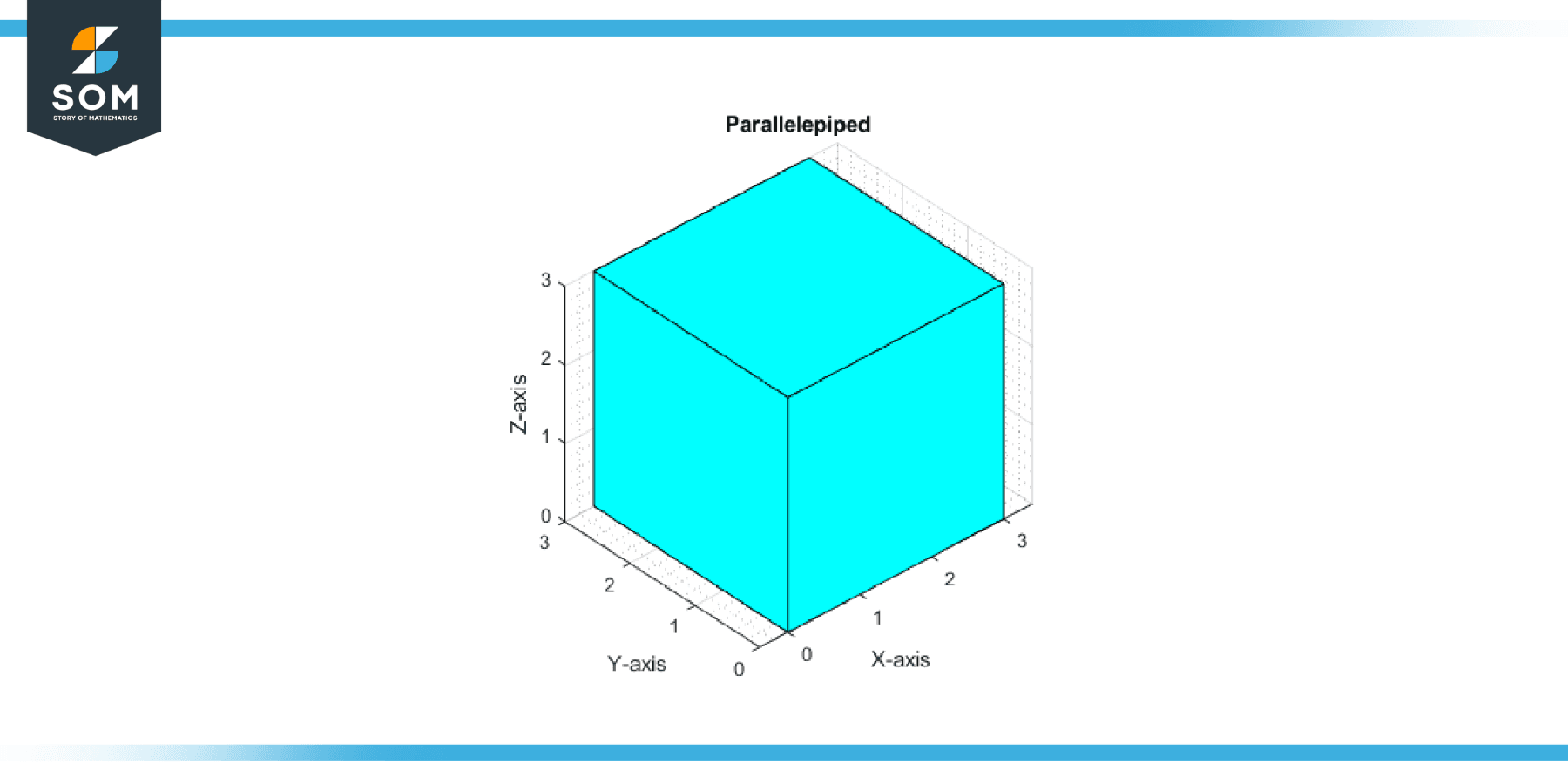
Figure-3.
Example 4
Given vectors a = [2, 2, 2], b = [1, 1, 1], and c = [3, 3, 3], find the volume of the parallelepiped spanned by these vectors.
Solution
Calculate the volume using the scalar triple product:
V = |a . (b x c)|
First, find the cross product b x c:
b x c = [(1)(3) – (1)(3), (1)(3) – (1)(3), (1)(3) – (1)(3)]
b x c = [0, 0, 0]
The dot product of vector a and the result is then zero, because the cross product is zero vector:
a . (b x c) = (2)(0) + (2)(0) + (2)(0)
a . (b x c) = 0
The volume of the parallelepiped is the absolute value of this result:
V = |0| = 0
The vectors are coplanar.
Example 5
Given vectors a = [-1, 2, -3], b = [4, -5, 6], and c = [-7, 8, -9], find the volume of the parallelepiped spanned by these vectors.
Solution
Calculate the volume using the scalar triple product:
V = |a . (b x c)|
First, find the cross product b x c:
b x c = [(-5)(-9) – (6)(8), (6)(-7) – (4)(-9), (4)(8) – (-5)(-7)]
b x c = [-3, 6, -3]
The dot product of vector a and the result is:
a . (b x c) = (-1)(-3) + (2)(6) + (-3)(-3)
a . (b x c) = 3 + 12 + 9
a . (b x c) = 24
The volume of the parallelepiped is the absolute value of this result:
V = |24| = 24
Example 6
Given vectors a = [1, 0, 2], b = [-1, 2, 1], and c = [0, 1, 1], calculate the volume of the parallelepiped spanned by these vectors.
Solution
Calculate the volume using the scalar triple product:
V = |a . (b x c)|
First, calculate the cross product b x c:
b x c = [(2)(1) – (1)(1), (1)(0) – (-1)(1), (-1)(1) – (2)(0)]
b x c = [1, 1, -1]
The dot product of vector a and the result is then:
a . (b x c) = (1)(1) + (0)(1) + (2)(-1)
a . (b x c) = 1 – 2
a . (b x c) = -1
The volume of the parallelepiped is the absolute value of this result:
V = |-1| = 1
All images were created with MATLAB.
