Perimeter of a Triangle – Explanation & Examples

The perimeter of a triangle can be defined as the total length across all the boundaries of a triangle.

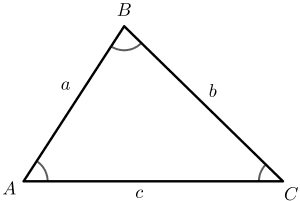
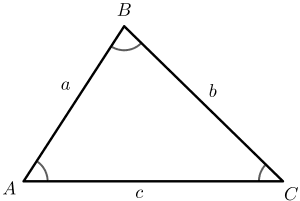
Let the lengths of three sides of a triangle be given as $a$, $b$ and $c$, as shown in the figure above. With this information, the perimeter is calculated as:

$Perimeter = a + b + c$

The triangle is a geometrical figure with three sides, and it can be further classified into different types depending upon the measurements of its sides and its angles. We will slightly modify the perimeter formula for each type of triangle. In this topic, we will discuss how to calculate the perimeter of different types of triangles.

Generally speaking, the perimeter will give you the total length of any given polygon. Perimeter is calculated by simply adding all the sides of a polygon. For a triangle, not all sides and angles need to be equal. The relationship between the angles and the sides varies with the type of triangle, so the perimeter formula will differ depending upon the type of triangle.

What Is the Perimeter of a Triangle?

The perimeter of a triangle is the sum of the length of its sides. To calculate the perimeter of a triangle, we have to calculate the total length across the boundaries of the triangle. Since the perimeter is calculated by doing addition, this makes the perimeter a linear measure.

Therefore, the units of the perimeter are the same as the unit of the given sides, i.e., centimeters, meters, inches, etc.

How To Find the Perimeter of a Triangle

To calculate the perimeter of a triangle, add all three sides of the triangle, as we discussed earlier.

Consider the picture of a triangle given below:

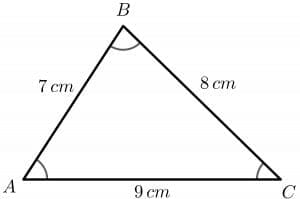
Here, the sides of the triangle are given as $7$, $8$, and $9$ cm, respectively. Hence the perimeter of this triangle will be given as:

Perimeter $= 7 + 8+ 9 = 24$ cm

Perimeter of a Triangle Formula

The formula for the perimeter of a triangle will depend on the type of triangle. Let us discuss the types of triangles and how to derive their formulas.

Types of Triangles

There are three different types of triangles depending on the relation between its sides.

1. Equilateral triangle
2. Isosceles triangle
3. Scalene triangle

– Equilateral Triangle

A triangle is considered to be an equilateral triangle if the lengths of all three sides are equal. For an equilateral triangle, the measure of each interior angle will be 60 degrees. The figure of an equilateral triangle is given below.

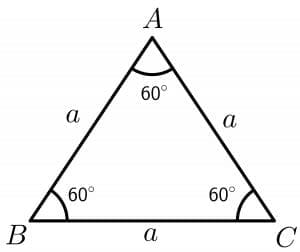
Perimeter of an Equilateral Triangle

An equilateral triangle is a triangle with three equal sides. So if the sides are $a$, $b$ and $c$, then we will write the perimeter of the triangle as

Perimeter of equilateral triangle $= a + b + c$

As we know that $a = b = c$, hence

Perimeter of equilateral triangle $= 3a = 3b = 3c$

Example 1:

If the value of one side of an equilateral triangle is 6cm, what will be the perimeter of the triangle?

Solution:

We are given the value of one side of the equilateral triangle, but as we know, all three sides of the equilateral triangle are equal. Hence the perimeter of the triangle will be calculated as follows:

Perimeter of equilateral triangle $= 3\times a$

Perimeter of equilateral triangle $= 3\times 6$

Perimeter of equilateral triangle $= 18cm$

– Isosceles Triangle

A triangle is called an isosceles triangle if the lengths and angles of two sides are equal to each other while the third side differs from the rest. The figure of an isosceles triangle is shown below.

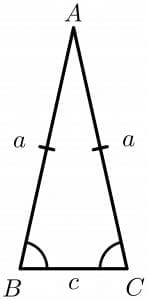
Perimeter of an Isosceles Triangle

An isosceles triangle is a triangle with two equal sides. So if the sides are $a$, $b$ and $c$ and $a = b$, then we will write the perimeter of the triangle as

Perimeter of triangle $= a + b + c$

Perimeter of isosceles triangle $= a + a + c$

Perimeter of isosceles triangle $= 2a + c$

Example 2:

If the perimeter of a triangle is 40 cm and the length of two of its sides is 8cm each, what will be the length of the third side of the triangle?

Solution:

We are given the value of two sides of the triangle that are equal; hence, it is an isosceles triangle.

Perimeter of an isosceles triangle $= 2a + b$

$48 = (2\times 8) + b $

$b = \dfrac{48}{16} $

$b = 3 cm $

– Scalene Triangle

A triangle is called a scalene triangle if the length of all three sides is different from each other. This means no side will be equal to any other side. For example, the figure of a scalene triangle below shows that none of its sides are equal.

Perimeter of a Scalene Triangle

A scalene triangle is one that has three different sides. Since all sides are different, we cannot modify the formula for the perimeter of the triangle as we did for the equilateral and the isosceles triangles. Hence, the formula remains the same as the standard one, i.e.,

Perimeter of triangle $= a + b + c$.

Example 3:

If the length of three sides of a triangle is 5cm, 6cm, and 4 cm respectively, what will be the perimeter of the triangle?

Solution:

As the length of all three sides of a triangle is different, it is a scalene triangle. The formula for the perimeter of the scalene triangle is given as

P $= a + b+ c$

$P = 5+6+4 $

$P = 15cm $

Perimeter of a Right Angle Triangle

A triangle is called a right-angle triangle if one of its angles is right. This means that one of the angles of the triangle is $90^{o}$. The perimeter of such a triangle is also calculated by adding all the sides of the triangle, so if the length of one of the sides is not available, then we can use the Pythagorean theorem to find that value. For example, consider a right triangle given below.

Here “b” is the base, “a” is perpendicular, and “c” is the hypotenuse.

In accordance with the definition of the Pythagorean theorem, the square of the hypotenuse is equal to the sum of the square of the base and perpendicular.

$c^{2} = a^{2}+b^{2}$

$c = \sqrt{(a^{2}+b^{2})}$

So if the value of the side “c” is unknown, then we can write the formula for the perimeter as

Perimeter of right triangle $= a+b+\sqrt{(a^{2}+b^{2})}$

Example 4: 

Consider a right angle triangle ABC where the side AC is the hypotenuse. If the measure of the sides AB and BC are 8 cm and 6 cm respectively, what will be the perimeter of the triangle?

Solution:

We need the values of all three sides to calculate the perimeter of the right triangle. As this is a right triangle, we can calculate the length of side AC using the Pythagorean theorem.

$AC^{2} = AB^{2}+BC^{2}$

$AC = \sqrt{(AB^{2}+BC^{2})}$

$AC = \sqrt{(8^{2}+6^{2})}$

$AC = \sqrt{64+36}$

$AC = \sqrt{100}$

$AC = 10 cm$

Perimeter $= AB + BC+ AC $

$ Perimeter = 8+6+10 $

$ Perimeter = 24 cm $

Perimeter of an Isosceles Right Angle Triangle

A triangle is called an isosceles right angle triangle if two sides and two angles are equal, and the third angle is a right angle. For example, consider the picture of an isosceles right triangle given below.

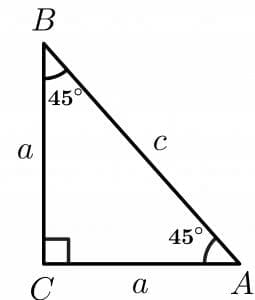
Here, the base and perpendicular are equal and denoted by “a”, while “c” is the triangle’s hypotenuse.

We will write the perimeter of the triangle as:

Perimeter of right triangle $= 2a+c$

If the hypotenuse of the triangle is not known, then it can be calculated using the Pythagorean theorem.

$c^{2} = a^{2}+b^{2}$

Here a = b

$c = \sqrt{(a^{2}+a^{2})}$

$c =\sqrt{(2\times a^{2})}$

$c = \sqrt{2}\times a $

Hence if the value of “c” is unknown, then we can write the formula as:

Perimeter of right triangle $= 2a+ \sqrt{2}\times a $

Example 5: 

Consider a triangle ABC. The length of the two sides AB and CA of the triangle is 8 cm each while the two angles are $45^{o}$ each. What will be the perimeter of the triangle?

Solution:

We know that the right-angled triangle in which two sides and two interior angles are equal is called an isosceles right-angle triangle. To calculate the perimeter of the triangle, we need to know the length of the third side. The length of the third side “BC” can be calculated using the formula:

$BC = \sqrt{2}\times AB $

$BC = 1.414 \times 8 $

$BC = 11.31 $ approx.

The perimeter of the triangle will be:

Perimeter $= 8 + 8 + 11.31 = 27.31 cm$ approx.

Practice Questions

1. Consider a triangle with sides $5cm$, $6cm$, and $8cm$. What will be the perimeter of the triangle?

2. If the three sides of a triangle are equal to $7 cm$, what will be the perimeter of the triangle?

3. Nathan is designing a triangular garden. Help Nathan calculate the perimeter of the garden using the data given below:

• The value of the lengths of the two sides are $= 6 cm$ each, and the interior angles are $45^{o}$ each.
• The value of the lengths of the two sides are $ 6 cm$ and $8 cm$. Therefore, one angle of the triangle is a right angle.
• The value of the lengths of the two sides are $= 6 cm$ each, and the length of the third side is $10 cm$

4. Alex is given a triangular-shaped wire which is $99 cm$ in length.

• Calculate the length of sides of the triangle if the triangle is equilateral.
• Calculate the length of the third side if the length of the remaining two sides is $30 cm$ each

Answer Key

1. We know the formula of the perimeter of the triangle:

Perimeter of triangle $= a+b+c$

Perimeter of triangle $= 5cm + 6cm + 8cm$

Perimeter of triangle $= 19 cm$

2. We know the formula of the perimeter of a triangle when all the sides are the same is given as:

Perimeter $= 3\times a$

Perimeter $= 3\times 7$

Perimeter $= 21 cm$.

3.

• Since the two angles of a triangle are equal to $45^{o}$, then the third must be $90^o$ as the sum of the three angles of a triangle is always equal to $180^o$. Hence, we have an as isosceles right triangle, and the length of the two sides is given as 6 cm each.

The first thing to do is to calculate the length of the third side.

Let side a and b = 6cm and we have to find the length of side “c” by using the Pythagorean theorem.

$c^{2} = a^{2}+b^{2}$

Here a = b

$c = \sqrt{(a^{2}+a^{2})}$

$c =\sqrt{(2\times a^{2})}$

$c = \sqrt{2}\times a $

$c = 1.41\times 6 $

$c = 8.46cm $

The perimeter of the triangle will be:

Perimeter $= 6 + 6 + 8.46 = 20.46 cm$ approx.

• One of the angle is $90^{o}$, so it is a right angle triangle.

We are given two sides and we have to calculate the length of the third side.

Let side a $= 5 cm$  and b $= 8 cm$ and we have to find the length of the side “c” by using the Pythagorean theorem.

$c^{2} = a^{2}+b^{2}$

$c = \sqrt{(a^{2}+b^{2})}$

$c =\sqrt{(5^{2}+8^{2})}$

$c = \sqrt{25+64}$

$c =\sqrt{89}$

$c = 9.43 cm$ approx.

Perimeter $= a + b+ c $

Perimeter $= 5+ 8 + 9.43 $

Perimeter $= 22.43 cm $ approx.

•  The length of two sides of the triangle are same while the length of third side is different, so it is an isosceles triangle. Let side “a” and “b” $= 6cm$ while the side “c” $= 10 cm$.

We can calculate the perimeter by using the formula:

Perimeter of triangle $ = a+b+c $

Here a = b

Perimeter of triangle $ = 2a +c $

Perimeter of triangle $ = (2 \times 6) + 10$

Perimeter of triangle $ = 12 + 10$

Perimeter of triangle $ = 22 cm$

4.

• We are given the total length of a triangular-shaped wire, so the perimeter of the triangular figure is 99 cm.

If all the sides of the triangle are equal, it is an equilateral triangle. The perimeter of an equilateral triangle is:

Perimeter $ = 3\times a $

99 $ = 3\times a $

a $ = \dfrac{99}{3} $

a $ = 33 cm $

So the length of all the sides of the triangle is 33cm each.

• We are given the total length of a triangular-shaped wire and the length of two sides of the triangle. The two sides of the triangle are equal, so it is an isosceles triangle. We can calculate the length of the third side by using the perimeter formula for an isosceles triangle.

Let $a = b = 30 cm$ and perimeter$ = 99cm$

Perimeter of an isosceles triangle $= 2a + c$

$99 = (2\times 30) + c$

$c = 99 – 60$

$c = 39cm$

Images/mathematical drawings are created using GeoGebray