Pythagorean Theorem – Explanation & Examples

The Pythagorean Theorem, also referred to as the ‘Pythagoras theorem,’ is arguably the most famous formula in mathematics that defines the relationships between the sides of a right triangle.

The theorem is attributed to a Greek mathematician and philosopher named Pythagoras (569-500 B.C.E.). He has many contributions to mathematics, but the Pythagorean Theorem is the most important of them.

Pythagoras is credited with several contributions in mathematics, astronomy, music, religion, philosophy, etc. One of his notable contributions to mathematics is the discovery of the Pythagorean Theorem. Pythagoras studied the sides of a right triangle and discovered that the sum of the square of the two shorter sides of the triangles is equal to the square of the longest side.

This article will discuss what the Pythagorean Theorem is, its converse, and the Pythagorean Theorem formula. Before getting deeper into the topic, let’s recall the right triangle. A right triangle is a triangle with one interior angle equals 90 degrees. In a right triangle, the two short legs meet at an angle of 90 degrees. The hypotenuse of a triangle is opposite the 90-degree angle.

What is the Pythagorean Theorem?

The Pythagoras theorem is a mathematical law that states that the sum of squares of the lengths of the two short sides of the right triangle is equal to the square of the length of the hypotenuse.

The Pythagoras theorem is algebraically written as:

a² + b² = c²

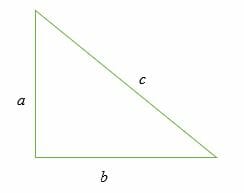
How to do the Pythagorean theorem?

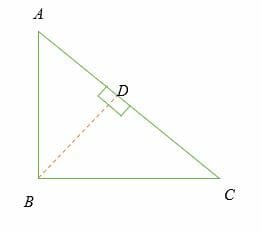
Consider a right triangle above.

Given that:

∠ ABC= 90°.

Let BD be the perpendicular line to the side AC.

Similar ∆s:

∆ADB and ∆ABC are similar triangles.

From the  similarity rule,

⇒ AD/AB = AB/AC

⇒ AD × AC = (AB) ² —————– (i)

Similarly;

∆BDC and ∆ABC are similar triangles. Therefore;

⇒ DC/BC = BC/AC

⇒ DC × AC = (BC) ² —————– (ii)

By combining equation (i) and (ii), we get,
AD × AC +  DC × AC = (AB) ² + (BC) ²

⇒ (AD + DC) × AC = (AB) ² + (BC) ²

⇒ (AC)² = (AB) ² + (BC) ²

Therefore, if we let AC = c; AB = b and BC = b, then;

⇒ c² = a² + b²

There are many demonstrations of the Pythagorean Theorem given by different mathematicians.

Another common demonstration is to draw the 3 squares in such a way that they form a right triangle in between, and the area of the bigger square (the one at hypotenuse) is equal to the sum of the area of the smaller two squares (the ones on the two sides).

Consider the 3 squares below:

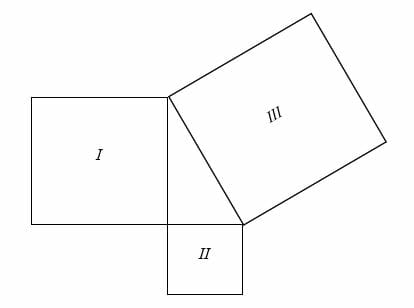
They are drawn in such a way that they form a right triangle. We can write their areas can in equation form:

Area of Square III = Area of Square I + Area of Square II

Let’s suppose the length of square I, square II, and square III are a, b and c, respectively.

Then,

Area of Square I = a ²

Area of Square II = b ²

Area of Square III = c ²

Hence, we can write it as:

a ² + b ² = c ²

which is a Pythagorean Theorem.

The Converse of the Pythagorean Theorem

The converse of the Pythagorean theorem is a rule that is used to classify triangles as either right triangle, acute triangle, or obtuse triangle.

Given the Pythagorean Theorem, a² + b² = c², then:

• For an acute triangle, c²< a² + b², where c is the side opposite the acute angle.
• For a right triangle, c²= a² + b², where c is the side of the 90-degree angle.
• For an obtuse triangle, c²> a² + b², where c is the side opposite the obtuse angle.

Example 1

Classify a triangle whose dimensions are; a = 5 m, b = 7 m and c = 9 m.

Solution

According to the Pythagorean Theorem, a² + b² = c² then;

a² + b² = 5² + 7² = 25 + 49 = 74

But, c² = 9² = 81
Compare: 81 > 74

Hence, c² > a² + b² (obtuse triangle).

Example 2

Classify a triangle whose side lengths a, b, c, are 8 mm, 15 mm, and 17 mm, respectively.

Solution
a² + b² = 8² + 15² = 64 + 225 = 289
But, c² = 17² = 289
Compare:289 = 289

Therefore, c² = a² + b² (right triangle).

Example 3

Classify a triangle whose side lengths are given as;11 in, 13 in, and 17 in.

Solution
a² + b² = 11² + 13² = 121 + 169 = 290
c² = 17² = 289
Compare: 289 < 290

Hence, c² < a² + b² (acute triangle)

The Pythagoras Theorem Formula

The Pythagoras Theorem formula is given as:

⇒ c² = a² + b²

where;

c = Length of the hypotenuse;

a = length of one side;

b = length of the second side.

We can use this formula to solve various problems involving right-angled triangles. For instance, we can use the formula to determine the third length of a triangle when the lengths of two sides of the triangle are known.

Application of Pythagoras Theorem formula in Real Life

• We can use the Pythagoras theorem to check whether a triangle is a right triangle or not.
• In oceanography, the formula is used to calculate the speed of sound waves in water.
• Pythagoras theorem is used in meteorology and aerospace to determine the sound source and its range.
• We can use the Pythagoras theorem to calculate electronic components such as tv screens, computer screens, solar panels, etc.
• We can use the Pythagorean Theorem to calculate the gradient of a certain landscape.
• In navigation, the theorem is used to calculate the shortest distance between given points.
• In architecture and construction,  we can use the Pythagorean theorem to calculate the slope of a roof, drainage system, dam, etc.

Worked examples of Pythagoras theorem:

Example 4

The two short sides of a right triangle are 5 cm and 12cm. Find the length of the third side

Solution

Given, a = 5 cm

b = 12 cm

c = ?

From the Pythagoras Theorem formula; c² = a² + b², we have;

c² = a² + b²

c² =12² + 5²

c² = 144 + 25

√c² = √169

c = 13.

Therefore, the third is equal to 13 cm.

Example 5

The diagonal and one side length of a triangular side is 25cm and 24cm, respectively. What is the dimension of the third side?

Solution

Using Pythagoras Theorem,

c² = a² + b².

Let b = third side

25² = 24² + b²
625 = 576 + b²
625 – 576 = 576 – 576 + b²
49 = b²
b ² = 49

b = √49 = 7 cm

Example 6

Find the size of a computer screen whose dimensions are 8 inches and 14 inches.

Hint: The diagonal of the screen is its size.

Solution

The size of a computer screen is the same as the diagonal of the screen.

Using Pythagoras Theorem,

c² = 8² + 15²

Solve for c.

c² = 64 + 225

c² = 289

c = √289

c = 17

Hence, the size of the computer screen is 17 inches.

Example 7

Find the right triangle area given that the diagonal and the bases are 8.5 cm and 7.7 cm, respectively.

Solution

Using Pythagoras Theorem,

8.5² = a² + 7.5²

Solve for a.

72.25 = a² + 56.25

72.25 – 56.25 = k² + 56.25 – 56.25

16 = a²

a = √16 = 4 cm

Area of a right triangle = (½) x base x height

= (½ x 7.7 x 4) cm²

= 15.4 cm²