The aim of this question is to find the surface corresponding to the Spherical Coordinates $p=sin\theta sin\phi$ by utilizing the Cartesian Coordinate system and Equation of Sphere.
First, we will explain the concept of Sphere, its Equation, and its Coordinates in the Cartesian Coordinate System.
A Sphere is defined as a $3D$ geometrical structure have a constant radius $\rho$ across all three dimensions and its center point is fixed. Therefore, the equation of sphere is being derived by considering the position coordinates of sphere centers with their constant radius $\rho$
\[{(x-a)}^2+{(y-b)}^2+{(z-c)}^2= \rho^2\]
This is the Equation of Sphere where
$Center = A(a, b, c)$
$Radius = \rho$
For a Standard Sphere in standard form, we know that the center has coordinates as $O(0,0,0)$ with $P(x,y,z)$ being any point on the sphere.
\[A(a, b, c) = O(0, 0, 0)\]
By substituting the coordinates of the center in the above equation we get:
\[{(x-0)}^2+{(y-0)}^2+{(z-0)}^2= \rho^2\]
\[x^2+y^2+z^2= \rho^2\]
In Cartesian Coordinate System, we convert the equation given in spherical coordinates to rectangular coordinates to identify its surface.
In physics, $\theta$ is defined as the Polar Angle (from the positive z-axis) and $\phi$ is defined as the Azimuthal Angle. By utilizing the concept of spherical coordinates, we know that a sphere having a radius is defined by 3 coordinates
\[x=\rho\ sin\theta\ cos\phi\]
\[y=\rho\ sin\theta\ sin\phi\]
\[z=\rho\ cos\theta\]
Expert Answer
Given As:
\[p= sin\theta\ sin\phi\]
By multiplying both sides with $\rho$, we get
\[\rho^2= \rho\ sin\theta\ sin\phi\]
As we know as per the Cartesian Coordinate System
\[y= \rho\ sin\theta\ sin\phi\]
Hence,
\[\rho^2=y\]
By substituting the value of $\rho^2$ in the Equation of Sphere, we get:
\[x^2+y^2+z^2 = y\]
\[x^2+y^2-y+z^2 = 0\]
Adding $\dfrac{1}{4}$ on both sides:
\[x^2+{(y}^2-y+\dfrac{1}{4})+z^2 = \dfrac{1}{4}\]
As we know that:
\[y^2-y+\dfrac{1}{4} = {(y-\dfrac{1}{2})}^2\]
By substituting the value in above equation
\[{(x-0)}^2+{(y-\dfrac{1}{2})}^2+{(z-0)}^2 = {(\dfrac{1}{2})}^2\]
By comparing it with the equation of sphere
\[{(x-a)}^2+{(y-b)}^2+{(z-c)}^2 = \rho^2\]
We get the coordinates for the center of the sphere and radius $\rho$ as follows:
\[Center\ A(a, b, c)=A(0, \dfrac{1}{2}, 0)\]
\[Radius\ \rho= \dfrac{1}{2}\]
Numerical Result
The surface that corresponds to $p=sin\theta sin\phi$ is a Sphere with $Center\ A(a, b, c)=A(0, \dfrac{1}{2}, 0)$ and $Radius\ \rho=\dfrac{1}{2}$.
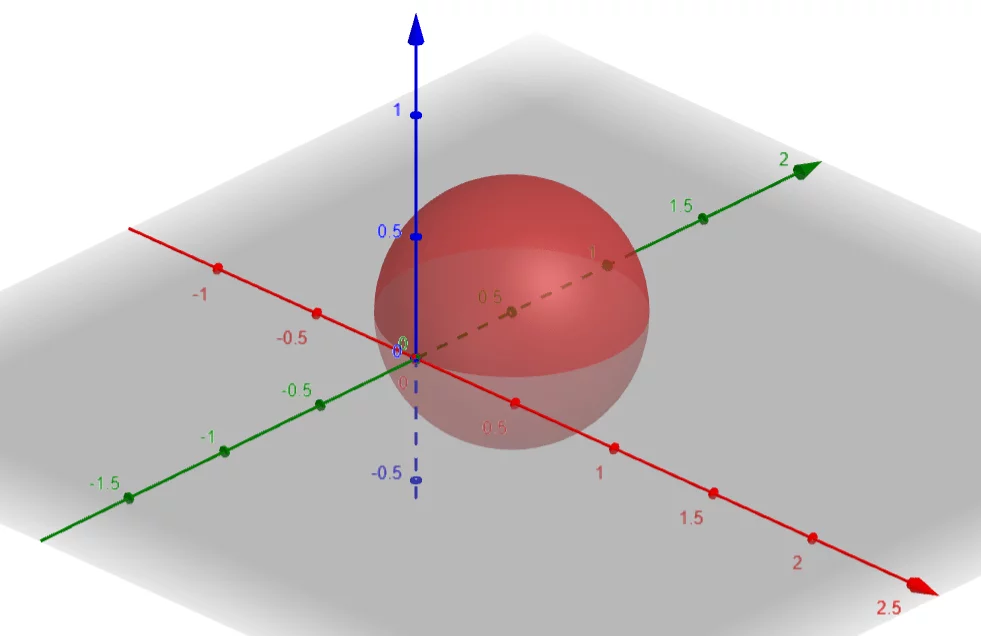Figure 1
Example
Identify the surface whose equation is given as $r = 2sin\theta$
We know that:
Cylindrical Coordinates $(r,\theta,z)$ with Center $A(a, b)$ are represented by equation:
\[{(x-a)}^2+{(y-b)}^2 = r^2\]
\[\tan{\theta = \dfrac{y}{x}}\]
\[z=z\]
Where:
\[x= rcos\theta\]
\[y= rsin\theta\]
Given that:
\[r= 2sin\theta\]
\[r^2=4\sin^2\theta\]
\[r^2=2sin\theta\times2sin\theta=2sin\theta\times \ r=2rsin\theta\]
Substituting the value of $y=rsin\theta$, we get
\[r^2=2y\]
Putting the value in the equation of Cylindrical Coordinates, we get
\[x^2+y^2=2y\]
\[x^2+y^2-2y=0\]
Adding $1$ on both sides
\[x^2+(y^2-2y+1)=1\]
\[x^2+(y^2-2y+1)=1\]
As we know that:
\[y^2-2y+1={(y-1)}^2\]
By substituting the value in the above equation
\[{(x-0)}^2+{(y-1)}^2=1\]
We get the coordinates for the center of the circle and radius $r$ as follows:
\[Center\ A(a,b)=A(0,1)\]
\[Radius\ r=1\]
Hence, the surface that corresponds to $r=2sin\theta$ is a circle with $Center\ A(a,b)=A(0,1)$ and $Radius\ r=1$.
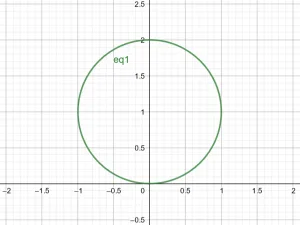Figure 2
Image/Mathematical drawings are created in Geogebra.