
This question aims to find the second derivative of the given implicit function. A function’s derivatives describe the rate of change of that function at a given point.
If the dependent variable, say $y$, is a function of the independent variable, say $x$, we usually express $y$ in terms of $x$. When this occurs, $y$ is said to be an explicit function of $x$.
For instance, when we express $y=x^2+2x$, this means we are defining $y$ explicitly in terms of $x$. If the relation between the values $y$ and $x$ is depicted by an equation where $y$ is not completely stated in terms of $x$, the equation is said to implicitly define $y$ in terms of $x$. The equation $\cos(y)+y=x^2+3$ is an example of an implicit equation.
We can use implicit differentiation to find slopes of tangents to curves that are explicitly not functions. This means that some components of $y$ are the functions that satisfy the given equation, but $y$ itself is not a function of $x$. The Chain Rule-based technique of implicit differentiation is used to find a derivative in the case when the relation between the variables is expressed implicitly rather than explicitly.
Expert Answer
The given equation is:
$xy+6e^y=6e$ $(1)$
Put $x=0$ in $(1)$
$(0)y+6e^y=6e$
$\implies 6e^y=6e\implies e^y=e$
$\implies y=1$
Hence, we have $y=1$ for $x=0$.
Now, differentiating both sides of $(1)$ with respect to $x$, we get:
$xy’+y+6e^yy’=0$ $(2)$
Putting $x=0$ and $y=1$ in $(2)$, we obtain:
$(0)y’+1+6e^{1}y’=0$
$\implies 1+6ey’=0$
$\implies y’=\dfrac{-1}{6e}$
Differentiating both sides of $(2)$ again with respect to $x$, we get:
$xy”+y’+y’+6e^yy”+y’6e^yy’=0$
$\implies xy”+6e^yy”+2y’+6e^y(y’)^2=0$ $(3)$
Plugging the values of $x,y$ and $y’$ in $(3)$, we get
$(0)y”+6e^{1}y”+2\left(\dfrac{-1}{6e}\right)+6e^{1}\left(\dfrac{-1}{6e}\right)^2=0$
$\implies 6ey”-\dfrac{1}{3e}+\dfrac{1}{6e}=0$
$\implies 6ey”-\dfrac{1}{6e}=0$
$\implies 6ey”=\dfrac{1}{6e}$
$\implies y”=\dfrac{1}{36e^2}$
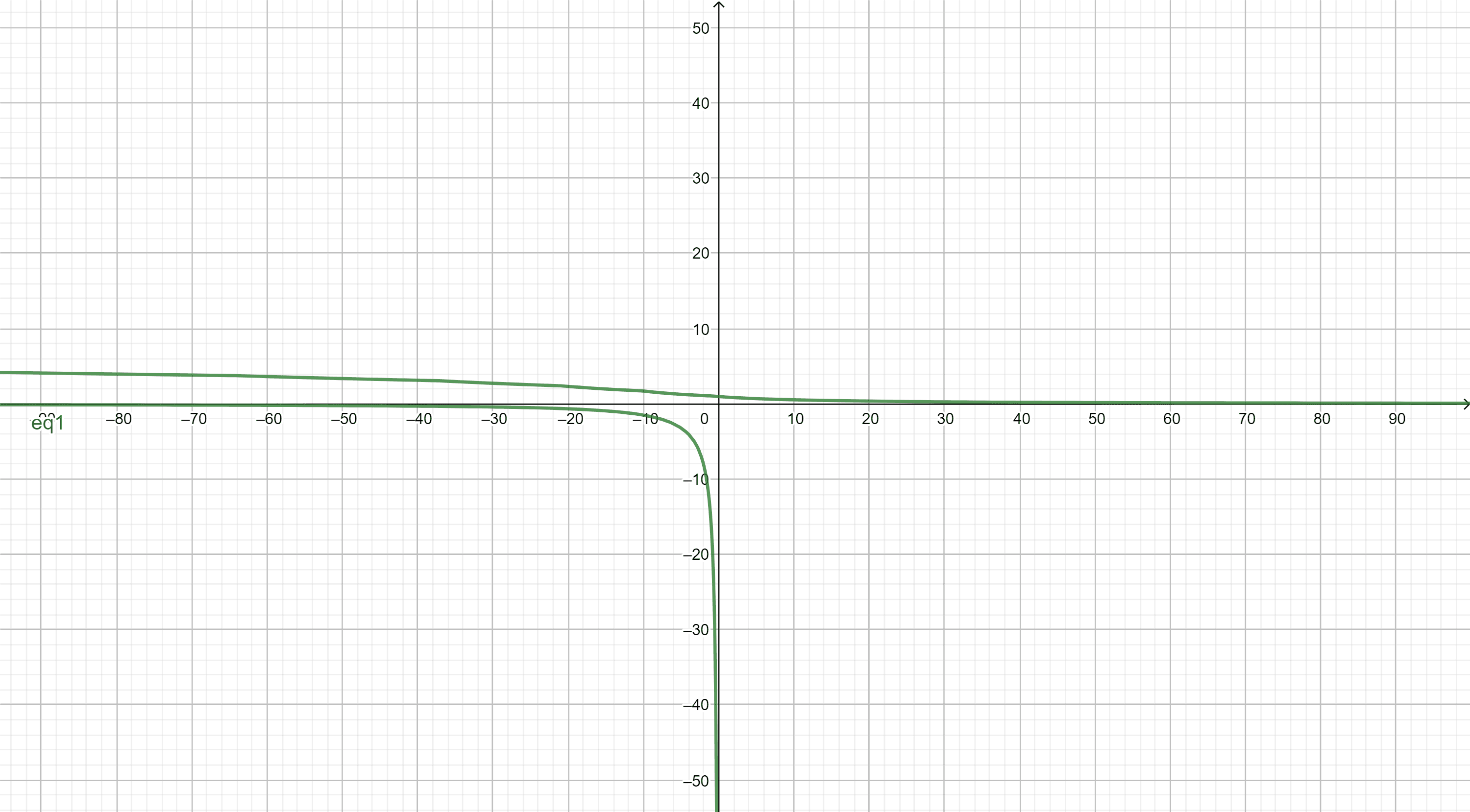
Graph of the given implicit equation:
Example
Find $y”$ when $x^2+y^2=4$.
Solution
Differentiating the given equation with respect to $x$, we get:
$2x+2yy’=0$
$\implies y’=-\dfrac{x}{y}$ $(1)$
Differentiating $(1)$ again with respect to $x$, we get:
$y”=-\dfrac{y\cdot1-xy’}{y^2}$
$\implies y”=-\dfrac{y-xy’}{y^2}$ $(2)$
Substituting $(1)$ in $(2)$
$y”=-\dfrac{y-x\left(-\dfrac{x}{y}\right)}{y^2}$
$\implies y”=-\dfrac{y^2+x^2}{y^3}$
Images/mathematical drawings are created with GeoGebra.
