
The aim of this question is to introduce the concept of congruency of an integer with another integer under some modulo.

Division
Whenever we divide one integer over another, we have two results, namely a quotient and a remainder. The quotient is the part of the result that defines the perfect division while the existence of the remainder signifies that the division was not perfect.
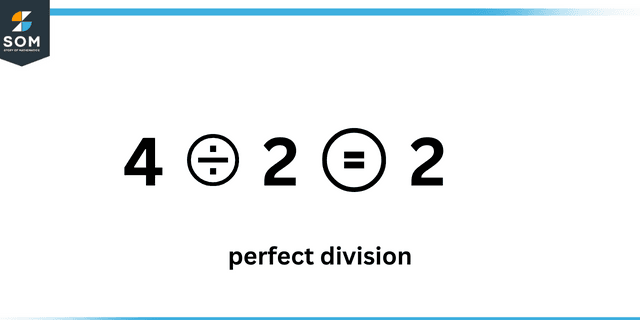
Perfect division
Let’s say we have three integers a, b, and c. Now we say that a is congruent to b modulo c if $ a \ – \ b $ is perfectly divisible by $ c $.
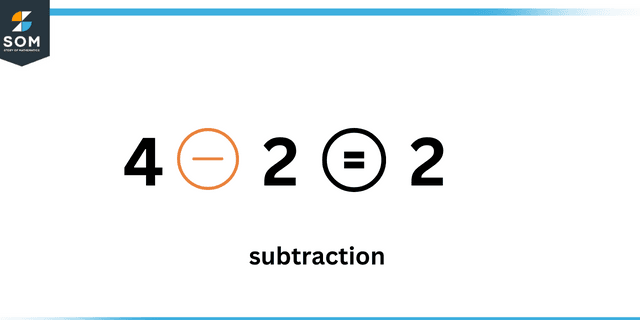
Subtraction
Expert Answer
Given that we need to find all integers (say $ x $) that are congruent to 4 modulo 12. In simpler words, we need to find the first five values of $ x \ – \ 4 $ that are perfectly divisible by $ 12 $.
To solve this question, we can take help from the integral multiples of $ 12 $ as listed below:
\[ \text{ Integral multiples of } 12 \ = \ \{ 0, \ 12, \ 24, \ 36, \ 48, \ 60, \ … \ … \ … \ \} \]
To find the first five integer values that are congruent to 4 modulo 12, we simply need to solve the following equations:
\[ \begin{array}{ c } \text{ Integers congruent } \\ \text{ to } 4 \text{ modulo } 12 \end{array} \ = \ \left \{ \begin{array}{ c c c } x \ – \ 4 \ = \ 0 & \Rightarrow & x \ = \ 0 \ + \ 4 & \Rightarrow & x \ = \ 4 \\ x \ – \ 4 \ = \ 12 & \Rightarrow & x \ = \ 12 \ + \ 4 & \Rightarrow & x \ = \ 16 \\ x \ – \ 4 \ = \ 24 & \Rightarrow & x \ = \ 24 \ + \ 4 & \Rightarrow & x \ = \ 28 \\ x \ – \ 4 \ = \ 36 & \Rightarrow & x \ = \ 36 \ + \ 4 & \Rightarrow & x \ = \ 40 \\ x \ – \ 4 \ = \ 48 & \Rightarrow & x \ = \ 48 \ + \ 4 & \Rightarrow & x \ = \ 52 \end{array} \right. \]
\[ \text{ Integers congruent to } 4 \text{ modulo } 12 \ = \ \{ 4, \ 16, \ 28, \ 40, \ 52 \ \} \]
Numerical Results
\[ \text{ Integers congruent to } 4 \text{ modulo } 12 \ = \ \{ 4, \ 16, \ 28, \ 40, \ 52 \ \} \]
Example
List down the first six integers such that they are congruent to 5 modulo 15.
Here:
\[ \text{ Integral multiples of } 15 \ = \ \{ 0, \ 15, \ 30, \ 45, \ 60, \ 75, \ … \ … \ … \ \} \]
So:
\[ \begin{array}{ c } \text{ Integers congruent } \\ \text{ to } 5 \text{ modulo } 15 \end{array} \ = \ \left \{ \begin{array}{ c c c } x \ – \ 5 \ = \ 0 & \Rightarrow & x \ = \ 0 \ + \ 5 & \Rightarrow & x \ = \ 5 \\ x \ – \ 5 \ = \ 15 & \Rightarrow & x \ = \ 15 \ + \ 5 & \Rightarrow & x \ = \ 20 \\ x \ – \ 5 \ = \ 30 & \Rightarrow & x \ = \ 30 \ + \ 5 & \Rightarrow & x \ = \ 35 \\ x \ – \ 5 \ = \ 45 & \Rightarrow & x \ = \ 45 \ + \ 5 & \Rightarrow & x \ = \ 50 \\ x \ – \ 5 \ = \ 60 & \Rightarrow & x \ = \ 60 \ + \ 5 & \Rightarrow & x \ = \ 65 \end{array} \right. \]
\[ \text{ Integers congruent to } 5 \text{ modulo } 15 \ = \ \{ 5, \ 20, \ 35, \ 50, \ 65 \ \} \]
