Sin^-1 x – Detailed Explanation and Examples

The function $sin^{-1}x$, also known as the inverse sine function, is an inverse form of a trigonometric function, and theoretically, we call it a sine inverse “x” function.

It can also be written as arc $sin(x)$ or can be read as arc of $sin(x)$ function. This function represents the inverse of the original sin(x) function.

In this topic, we will study what is meant by the sine inverse function, and we will also discuss the domain and range of sin^{-1}x and how we can calculate the derivative and integral of this function. We will also discuss some solved numerical examples for a better understanding of this topic.

What Is Meant by Sin^-1 x?

The $sin^{-1}x$ function is one of the six trigonometric functions and is called the inverse of the sine x function, while it is also written as arc sin(x) or a sin(x). We know that there are six trigonometry functions sine, cosine, tangent, cosecant, secant and cotangent. When we take the inverse of these functions, then we will get the inverse trigonometric functions.

A normal function of sine x is represented as $f(x) = y = sin x$, so when we want to take the inverse, it will be written as x = $sin^{-1}y$. The variable “y” is mostly used as the dependent variable while variable “x” is the independent variable when determining the domain and range of any function. The mathematical form of this function is written as:

$y = sin^{-1}x$

Sin^-1 x and Right Angle Triangle

The trigonometric sin^{-1}x is an essential function to determine the missing angles of a right-angle triangle. We know that the formula for sin x for a right-angle triangle is given as:

$Sin x = \dfrac{Perpendicualr}{Hypotenuse}$

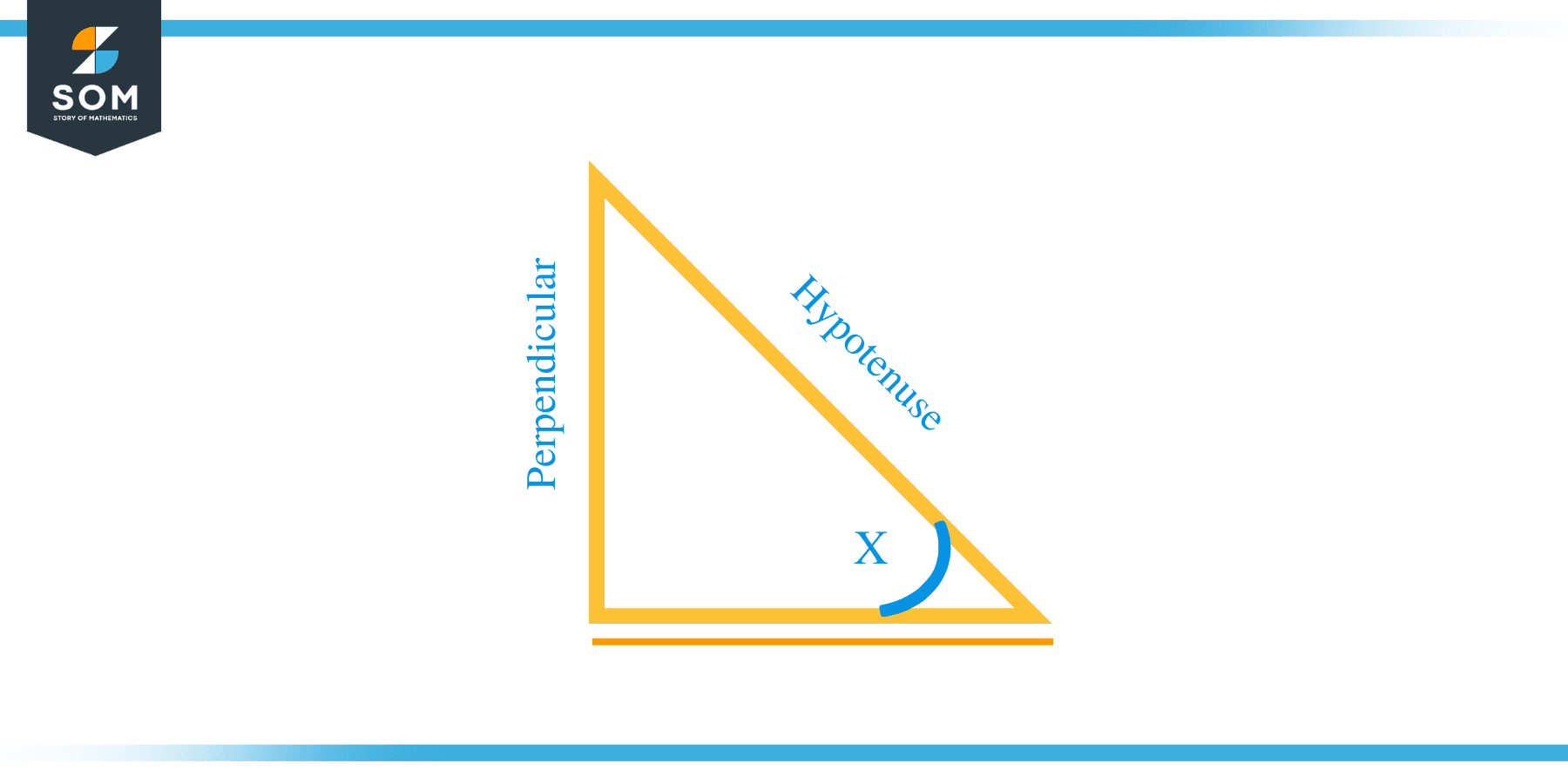
If we want to determine the missing angle or value of “x”, then we will use the inverse sin x to determine the missing angle:

$x = sin^{-1}\dfrac{Perpendicualr}{Hypotenuse}$

As we can see from the picture of the right angle triangle given below, we can measure the angle “x” by using the sin inverse function. This function can be used to determine any angle of a right-angle triangle provided that the desired data is available and the angle should lie within the limits of the sin inverse function (i.e. in the range of the sine inverse function).

The inverse sin function can be used to determine the unknown angles of other triangles as well by using the sine law. We know that according to sine law, if we are given a triangle XYZ, then let us assume the measure of the sides can be given as XY = x, YZ = y and ZX = z; then according to the law of sines:

$\dfrac{Sin X}{y} = \dfrac{Sin Y}{z}$

$Sin X = y \times \dfrac{Sin Y}{z}$

$X = sin^{-1}[ y \times \dfrac{Sin Y}{z}]$

So we can use the law of sines to determine the unknown angles of any triangle if we are provided with the relevant data.

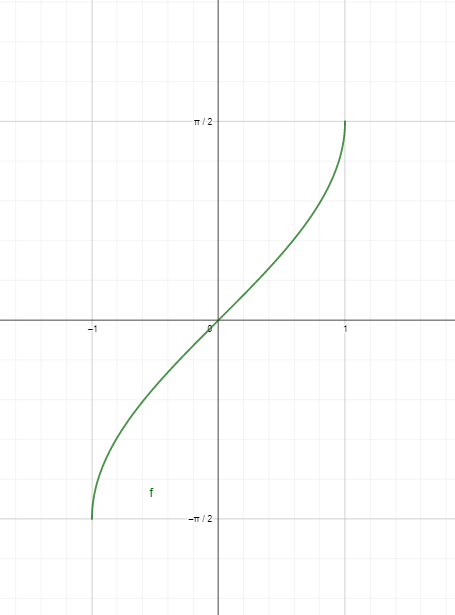
Sin^-1x Graph

The graph of $sin^{-1}x$ can be plotted by putting different values of “x” within the limit of -1 to 1. This limit is basically the domain of the function, and the corresponding output values are the range of the function; we will discuss the domain and range of sin inverse x in the next section. Let us take different values “x” of within limits and calculate the values of $sin^{-1}x$; after calculating the values, we join the points to form the function’s graph.

By plotting and joining the above points, we will get the graph of $sin^{-1}x$, and as you can see from the graph given below, the upper and lower limit of the y-axis are $\dfrac{\pi}{2}$ and $-\dfrac{\pi}{2}$ while the upper and lower limits for x-axis are 1 and -1, respectively. These are the range and domain of the said function. Let us discuss the domain and range of $sin^{-1}x$.

Domain and Range of Sin^-1x

The domain and range of sin^{-1}x are basically the possible input and out values of the independent and dependent variables, respectively. The domain of the function will be the possible input values. For a simple sin(x) function, the domain of the function consist of all the real numbers, while the range of a function is given as $[1,-1]$. This means that no matter what the input value is, it will lie between $1$ and $-1$.

We know that if the inverse of a function exists, then the range of the original function will be the domain of the inverse function. So in this case, the domain of the function $sin^{-1}x$ will be $[1,-1]$, so this means “x” can only have the values from -1 to 1 because at all other values the function will be undefined.

The range of $sin^{-1}x$ will only contain the defined values and these values are attainable when the value of “x” lies from 1 to -1. The maximum and minimum output value for $sin^{-1}x$ are $\dfrac{\pi}{2}$ and $-\dfrac{\pi}{2}$. Hence, the range of $sin^{-1}x$ can be written as $[-\dfrac{\pi}{2}$, $\dfrac{\pi}{2}]$.

Domain of $sin^{-1}x = [-1,1]$

Range $of sin^{-1}x = [-\dfrac{\pi}{2}$, $\dfrac{\pi}{2}]$

How To Solve for Sin^-1x

The steps for solving the function $sin^{-1}x$ or questions which involve this function are given below:

1. The domain of the function is $[1,-1]$; this means we will only calculate the function for input values which lies within the domain.
2. The range of the function is $[-\dfrac{\pi}{2}, \dfrac{\pi}{2}]$, so the output value or answer should lie in between the range, otherwise, our answer or calculation is incorrect.
3. We write the function as $y = sin^{-1}x$ so we can write it as $x = sin y$; we know that value of y will lie between $[-\dfrac{\pi}{2}$, $\dfrac{\pi}{2}]$ so the value of “y” which will satisfy the equation x = sin y will be our answer.

Example 1: Solve the following $sin^{-1}x$ functions:

1. $y = sin^{-1} (0.7)$
2. $y = sin^{-1} (-0.3)$
3. $y = sin^{-1} (-1.5)$
4. $y = sin^{-1} (1)$

Solution:

1).

We can write it as $sin y = 0.7$

You can now solve for the value of “y” by using the trigonometric table, and the answer is:

$Sin^{-1}(0.7) = 44.42^{o}$. We know that $\dfrac{\pi}{2} = 90^{o}$ and $-\dfrac{\pi}{2} = -90^{o}$. So our answer lies within the range.

2).

$y = sin^{-1} (-0.3) = -17.45^{o}$

3).

$y = sin^{-1} (-1.5) $= undefined. The output does not lie in the range; hence it is undefined.

4).

$y = sin^{-1} (1) = \dfrac{\pi}{2} = 90^{o}$.

Derivative of Sin^-1 x

The derivative of $y= sin^{-1}x$ or $f(x)=sin^{-1}x$ or sin inverse 1 x is $\dfrac{1}{\sqrt{1 – x^{2}}}$. The derivative of sin inverse x can be determined easily by using the chain rule of differentiation.

$y=sin^-1(x)$

$x = sin y$

Differentiating both sides with respect to “x.”

$\dfrac{d}{dx} x = \dfrac{d}{dx} sin(y)$

$1 = cosy . \dfrac{dy}{dx}$

$\dfrac{dy}{dx} = \dfrac{1}{cos(y)}$

We know from trigonometric identities that:

$sin^{2}x + cos^{2}x = 1$

$cos^{2}x = 1 – sin^{2}x$

$cos x = \sqrt{1 – sin^{2}x}$

So $cos y = \sqrt{1 – sin^{2}y}$

$\dfrac{dy}{dx} = \dfrac{1}{\sqrt{1 – sin^{2}y}}$

If $x = sin y$ then $x^{2} = sin^{2} y$

$\dfrac{d}{dx} sin^{-1}x = \dfrac{1}{\sqrt{1 – x^{2}}}$

Hence, we have proved that the derivative of $sin^{-1}x$ is $\dfrac{1}{\sqrt{1 – x^{2}}}$.

Example 2: Find the derivative of $4x.sin^{-1}(x)$.

Solution:

By using the chain rule, we will find out the derivative of $4x.sin^{-1}(x)$.

$\dfrac{d}{dx} 4x.sin^{-1}( x ) = \dfrac{d}{dx} 4x. sin^{-1}x + 4x. \dfrac{d}{dx} sin^{-1}x$

$\dfrac{d}{dx} 4x.sin^{-1}(x) = 4. sin^{-1}x + 4x. \dfrac{1}{\sqrt{1 – x^{2}}}$

$\dfrac{d}{dx} 4x.sin^{-1}(x) = 4. [ sin^{-1}x + \dfrac{x}{\sqrt{1 – x^{2}}}]$

Sin^-1x Integration

The integral of $sin^{-1}x$ is $x.sin^{-1}x+ \sqrt{1 – x^{2}}+ c$. The integral of sin inverse x can easily be determined by using integration by parts or the substitution method of integration. We will determine the integral of $sin^{-1}x$ by using the integration by parts method.

$\int sin^{-1}x. dx = \int sin^{-1}x. 1 dx$

$\int sin^{-1}x. dx = sin^{-1x} \int 1.dx – \int [ \int dx . \frac{d}{dx} sin^{-1}x] dx$

$\int sin^{-1}x. dx =x.sin^{-1}x – \int x. \dfrac{1}{\sqrt{1 – x^{2}}} dx$

Multiplying and dividing the second expression side by “$-2$”

$\int sin^{-1}x. dx = \int sin^{-1}x. dx =x.sin^{-1}x + \int \dfrac{\frac{1}{2}}{\sqrt{1 – x^{2}}}. -2x. dx$

$\int sin^{-1}x. dx = x sin^{-1}x + \frac{1}{2}\times \dfrac{\sqrt{1-x^{2}}}{\frac{1}{2}} + c$

$\int sin^{-1}x. dx = x.sin^{-1}x+ \sqrt{1 – x^{2}}+ c$

Example 3: Find the integral of $5.sin^{-1}(x)$.

Solution:

We have to evaluate $\int 5.sin^{-1}x dx$

$\int 5.sin^{-1}x dx = 5 \int sin^{-1}x dx$

We know that the integral of $\int sin^{-1}x is equal to x.sin^{-1}x+ \sqrt{1 – x^{2}}+ c$.

$\int 5.sin^{-1}x dx = 5 [x.sin^{-1}x+ \sqrt{1 – x^{2}}+ c]$

Different Formulas of Sin^-1 x

The function of $sin^{-1}x$ is utilized in various formulas, and all these formulas are essential for you to memorize as they are used in solving various differentiation and integral problems. We can also call these formulas as properties of $sin^{-1}x$. Some of the important formulas involving $sin^{-1}x$ are listed below.

1. $Sin^{-1}(-x) = -sin^{-1}x$
2. $Sin(sin^{-1}x) = 1$, when domain is $[-1,1]$
3. $Sin^{-1}(\frac{1}{x}) = cosec^{-1}x$
4. $Sin^{-1}x + Cos^{-1}x = \dfrac{\pi}{2}$, when domain is $[-1,1]$.

Practice Questions:

1. If the length of the perpendicular and hypotenuse of a right angle triangle is four units and six units, respectively, then what will be the corresponding angle “x?”
2. Find the derivative of sin inverse x^2.

Answer Key:

1).

We know that the formula for sin x for a right-angle triangle is:

$sin x = \dfrac{Perpendicular}{Hypotenuse}$

$sin x = \dfrac{4}{6} = 42.067^{o}$

2).

The derivative of $sin^{-1}x^{2} is \dfrac{2x}{\sqrt{1-x^{4}}}$.